重回帰分析 - 統計学入門一歩先へ

はじめに

以前、1個の説明変数を使って関心ある変数を表現する単回帰モデルについて、基本的な概念と推定方法を説明した。
単回帰分析(1)大雑把な説明 - 統計学入門一歩先へ
 単回帰分析(2)モデルの定式化と最小二乗法 - 統計学入門一歩先へ
 単回帰分析(3)最尤法による推定 - 統計学入門一歩先へ
しかしながら、単回帰モデルのようなシンプルすぎるモデルでは物足りないことが多くある。今後の予測が目的であればできるだけ多くの情報が必要かもしれないし、説明変数の影響の大きさを評価したい場合にはいくつかの変数について「調整」をしなければ正しい結論が得られないこともある。そこで、複数の説明変数を使って関心のある変数を説明するモデルを構成したい。このようなモデルを用いた分析を「重回帰分析(Multiple regression)」という。
今回は重回帰分析の数学モデルについて簡単に触れ、例題を見ながら解釈のしかたを確認していこうと思う。

重回帰分析モデル

単回帰分析では、目的変数 $y$ を1つの説明変数 $x$ を使って

$\displaystyle y = \beta_0 + \beta_1 x + \varepsilon$

のようにモデル化するのであった。 $\varepsilon$ はモデルで説明できないランダムな誤差で、正規分布に従うものとする。 $\beta_0$ は直線の切片、 $\beta_1$ は直線の傾き（=説明変数 $x$ 「1単位」が目的変数 $y$ に与える効果を示す）である。
重回帰分析では、 $y$ を説明するために複数の変数 $x_1, \cdots, x_p$ を用いる：

$\displaystyle y = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \cdots + \beta_p x_p + \varepsilon.$

$\beta_1$ から $\beta_p$ はそれぞれ、説明変数 $x_1$ から $x_p$ が $y$ へ与える効果の大きさを表す。 $\varepsilon$ は単回帰モデルと同様、正規分布に従う誤差である。誤差を除いた部分である $\beta_0 + \beta_1 x_1 + \beta_2 x_2 + \cdots + \beta_p x_p$ が、目的変数 $y$ の説明変数 $x_1, \cdots, x_p$ を与えたもとでの条件付き期待値を表しているという点も単回帰分析と同様である。
モデルのパラメータ（未確定の値） $\beta_0, \beta_1, \cdots, \beta_p$ を最もデータに適合するように決定するためには、これも単回帰分析の場合と同様に最小二乗法、または最尤法を用いる。なお、重回帰分析の場合にはパラメータの数が多いので、行列を用いた表現で解を表すことが多い。
まず、説明変数 $x_1, \cdots, x_p$ とパラメータ $\beta_0, \beta_1, \cdots, \beta_p$ をそれぞれベクトルで表そう。

$\displaystyle \boldsymbol{x} = (1, x_1, \cdots, x_p)^T, \\ \boldsymbol{\beta} = (\beta_0, \beta_1, \cdots, \beta_p)^T$

このようにすると重回帰モデルは $y = \boldsymbol{x}^T \boldsymbol{\beta} + \varepsilon$ と書ける。切片 $\beta_0$ を考慮するためにベクトル $\boldsymbol{x}$ には「1」を含めていることに注意されたい。
さて、サンプルサイズをNとすると、目的変数と説明変数ベクトルはそれぞれ $y_1, \cdots, y_N$ 、 $\boldsymbol{x}_1. \cdots, \boldsymbol{x}_N$ のN個が存在するので、重回帰モデルの等式もN個必要になる。目的変数をベクトル $\boldsymbol{y} = (y_1, \cdots, y_N)$ とし、説明変数を行列 $X = (\boldsymbol{x}_1, \cdots, \boldsymbol{x}_N)^T$ 、誤差を $\boldsymbol{\varepsilon} = (\varepsilon_1, \cdots, \varepsilon_N)$ と表すことにすると、重回帰モデルは以下のようにまとめられる。

$\displaystyle \boldsymbol{y} = X \boldsymbol{\beta} + \boldsymbol{\varepsilon}.$

ここからは線形代数の計算が必要になるが、最小二乗法でも最尤法でも、パラメータの推定量は次のようになる。

$\displaystyle \hat{\boldsymbol{\beta}} = (X^T X)^{-1} X^T \boldsymbol{y}.$

（もちろん、実用上は手計算をする必要はない）

結果の解釈

では、このようにして推定されたモデルの結果をどのように解釈すればよいだろうか？ここでは、以前具体例として使った「中間テストと期末テストの得点の関係」をアレンジした例を使って考えてみたい。
今回は中間テストの得点（横軸）と期末テストの得点（縦軸）の間に以下のような関係がみられているとする。
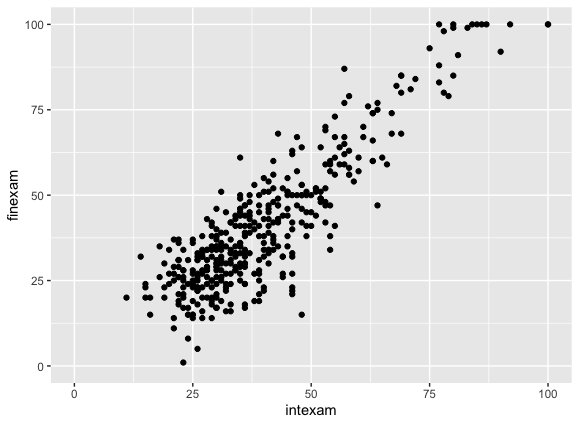
f:id:mstour:20201220211225p:plain
このデータに対して、期末テストの得点を目的変数、中間テストの得点を説明変数とする単回帰モデルを用いると、次のような直線が当てはめられる。
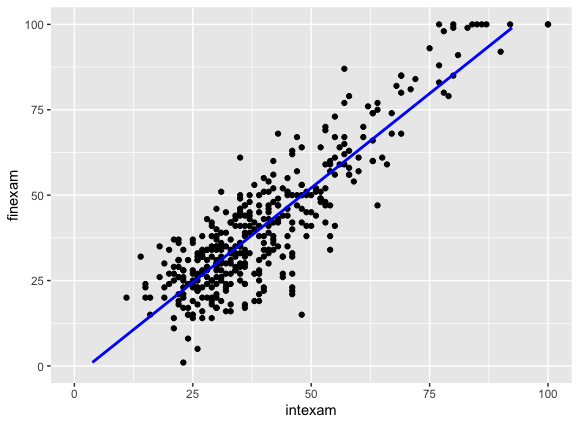
f:id:mstour:20201220211239p:plain
また、以下のアウトプットから、例えば中間テストの得点が10点上がるごとに期末テストの得点はおよそ11点上がる、という強い関係性が示唆される（「Coefficients:」の「intexam」の行のEstimateの値「1.10574」が、中間テストの得点が1点上がった時に期末テストの得点が何点上がっているかを表す）。

Call:
lm(formula = finexam ~ intexam, data = df)

Residuals:
    Min      1Q  Median      3Q     Max 
-34.903  -6.319   0.155   6.811  27.146 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) -3.17316    1.29697  -2.447   0.0149 *  
intexam      1.10574    0.03018  36.641   <2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 9.51 on 398 degrees of freedom
Multiple R-squared:  0.7713,	Adjusted R-squared:  0.7708 
F-statistic:  1343 on 1 and 398 DF,  p-value: < 2.2e-16

ということは、（単回帰の記事で登場した）この学生の言うように、中間テストの得点で期末テストの得点が決まってしまうことになり、勉強しても無駄なのだろうか？
f:id:mstour:20201108201820j:plain
ここで、「前期での1日あたり自主学習時間」というデータをとっていたとしよう。前期の自主学習時間と今期の中間テストの得点との相関をみてみると、次のようにかなり強い相関があったとする（intexamは中間テストの得点、studytimeは前期の自主学習時間）：

cor(df$intexam, df$studytime)
[1] 0.9107677

さらに、期末テストの得点との相関も次のようだったとする：

> cor(df$finexam, df$studytime)
[1] 0.9234282

素直に考えると、前期に自主学習を長い時間やっていた学生は今期の中間テストも、期末テストもよい成績になるという因果関係がありそうである（あくまで説明のための例ということで、かなり乱暴な議論であることをご了承いただきたい）。
整理すると、中間テストの得点と期末テストの得点の他に、第3の要因「前期の学習時間」があり、これはどちらの得点にも影響を与えていることがわかっている状況である。
f:id:mstour:20201222202134j:plain
このような時、「前期の学習時間」による交絡が起こり、これを抜きに考えると中間テストの得点と期末テストの得点の間の関係性が正しく評価できない可能性がある。そこで、「前期の学習時間」を説明変数に追加した重回帰分析を行うことで、「もしも前期の学習時間が同じだった時、中間テストの得点と期末テストの得点にはどの程度の関係があるか」を推定することができるようになる（前期の学習時間を「調整する」という言い方をする）。
実際にやってみると、以下のようになる。

Call:
lm(formula = finexam ~ intexam + studytime, data = df)

Residuals:
     Min       1Q   Median       3Q      Max 
-27.9823  -4.4413   0.6285   4.6273  23.9977 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 15.93312    1.56706  10.168  < 2e-16 ***
intexam      0.27491    0.05708   4.816 2.09e-06 ***
studytime    0.24215    0.01515  15.981  < 2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 7.428 on 397 degrees of freedom
Multiple R-squared:  0.8608,	Adjusted R-squared:  0.8601 
F-statistic:  1228 on 2 and 397 DF,  p-value: < 2.2e-16

「intexam」の行のEstimateの値は0.27491となり、前期の学習時間(studytime)を説明変数に入れなかった場合の1.10574とはかなり異なる結果になった。これは、「前期の学習時間が同じ人どうしで考えると」、中間テストの得点が10点上がっても、期末テストの得点は3点も上がらないことを意味する。つまり中間テストと期末テストの間には、単回帰分析でみられたような直接的な関係はあまりないということになる。
一方、「中間テストの得点が同じ人どうしで考えると」、前期の学習時間が1日あたり60分長かった場合、期末テストでは $60 \times 0.24 = 14.4$ 点ほど良い成績になっていたと推測できる・・・と言いたいところだが、
　・前期の学習時間→中間テスト→期末テスト
　・前期の学習時間→期末テスト
という2つの因果の経路がある場合、中間に位置する変数（中間テスト）をモデルに含めると前期の学習時間の効果は正しく推定できないことが知られている。このあたりの話は本題ではないのでこれ以上は述べないことにするが、もし前期の学習時間が期末テストに与える影響を調べたいのであれば、前期の学習時間だけを説明変数にすればよい。
このように、原因と思われる変数（ここでは中間テストの得点）と結果と思われる変数（ここでは期末テストの得点）の両方に影響を与えるような変数がある（交絡が存在する）場合には、重回帰分析を用いることでその影響を取り除いて評価することができる。ひとまず今回の例では、中間テストの得点と期末テストの得点との間には見かけだけの関連が生じていたに過ぎず、習慣的な勉強が影響していそうだとは言えそうである。
f:id:mstour:20201222202153j:plain

まとめ

今回は、重回帰分析のモデルの定義を説明し、単純な例を用いて結果の解釈について考えてみた。
今回の参考文献は以下の通り。
[1] 鈴木武, 山田作太郎(1996), "数理統計学", 内田老鶴圃.
[2] Annette J. Dobson(2008), "一般化線形モデル入門", 共立出版.
[3] 岩崎学(2015), "統計的因果推論", 朝倉書店.