単回帰分析(3)最尤法による推定 - 統計学入門一歩先へ

はじめに

前回は、単回帰分析モデルをデータに適合させるために、最適なパラメータを最小二乗法を用いて推定する方法を紹介した。今回は、最尤法(Maximum likelihood method)を用いた推定の話をしたいと思う。
前回少し述べたように、単回帰モデル

$\displaystyle E[ y | x ] = \alpha + \beta x$

の数式の中に現れるパラメータ（ $\alpha, \beta$ ）の推定結果は最小二乗法と最尤法とでは同じになる（ただし目的変数どうしは独立と仮定する）。とはいえ、単回帰で想定する「正規分布」以外の確率分布を考えたい場合には最尤法を使った方がよいので、ここで大まかな流れを述べておきたい。

最尤法って？

まず、何らかの独立なN個のデータ $y_1, \cdots, y_N$ を考えよう。とりあえずここでは日本人成人男性N人の身長とする。そして、これらのデータは正規分布に従ってばらついていると考えても妥当ということにしよう（身長はそう考えても差し支えないと思われる）。話を簡単にするために、N人のデータは互いに独立と考える（違う人どうしの身長なので、当たり前ではあるが）。
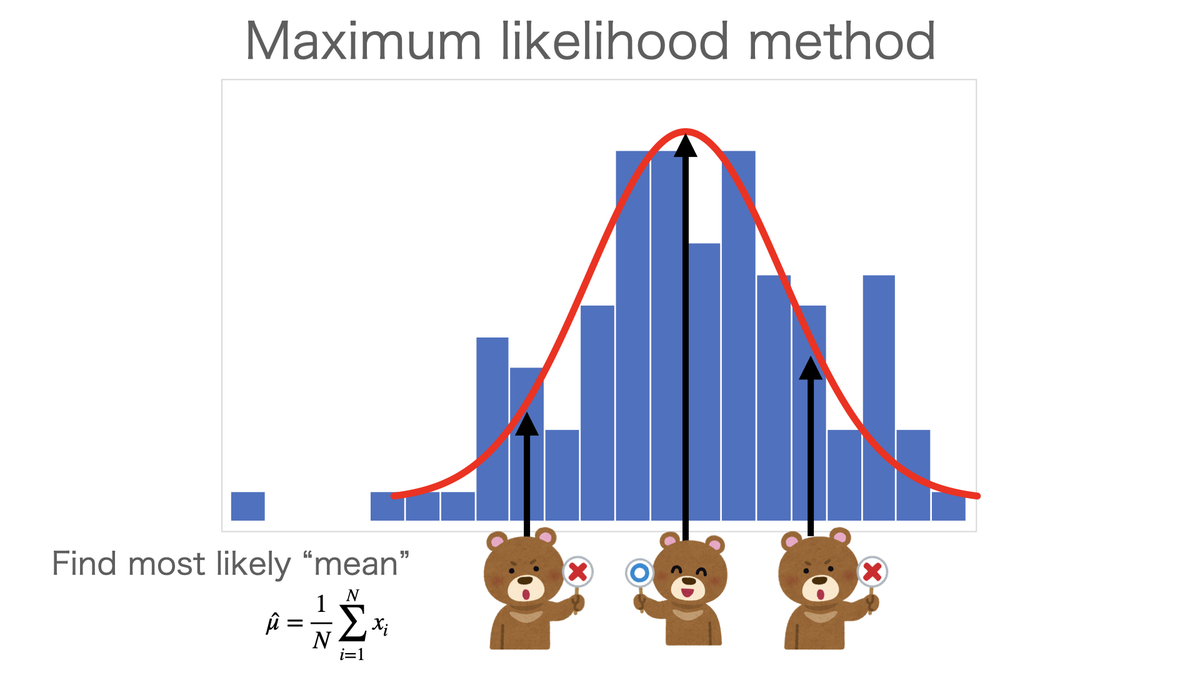
さて、今N人の身長データが手元にあり、ここから日本人成人男性の平均身長を推定することを考える。N人は日本人成人男性全員からランダムに選ばれたものと仮定しておく（そうではなくて例えば高齢者ばかりのデータを集めてきたとすると、全体の平均よりも身長の低い人が多い可能性がある。つまり、このデータから何らか物を言おうとすると結論にバイアスが生じることになる）。日本人成人男性の身長は正規分布に従ってばらついていると想定しているので、その正規分布の平均パラメータを平均身長として考えればよいだろう。そこで、手元のデータからうまく推定したい。最尤法は、手元のデータが得られる確率が一番大きくなるように未知のパラメータを決める方法である。
もう少し具体的に説明すると、個々のデータの確率密度関数（小難しい名前がついているが、要するにそのデータが得られる確率みたいなもの）をすべて掛け合わせたものが最大になるように計算する。この確率密度関数を掛け合わせたものを尤度関数(Likelihood function)という。 $i$ さんの身長の確率密度関数を $f(x_i | \mu, \sigma^2)$ とすると、尤度関数は

$\displaystyle L(\mu, \sigma^2 | x_1, \cdots, x_N) = \prod_{i=1}^{N} f(x_i | \mu, \sigma^2)$

と定義される。ただし $\mu$ は今考えている正規分布の平均パラメータ、 $\sigma^2$ は分散パラメータである。今関心があるのは身長の平均なので、平均パラメータ $\mu$ の推定だけを考えることにする。
上の式の右辺は、 $\mu$ と $\sigma^2$ が決まっていれば具体的な数値が出てくるのだが、今のところ両方とも分からない。一方でデータ $x_1, \cdots, x_N$ の値はわかっている。そこで、尤度関数 $L$ を $\mu$ と $\sigma^2$ の関数として考えて、手元にあるデータを前提としたときに関数の値が最大になるように $\mu$ と $\sigma^2$ を決める。一応関数を最大化する解を求めるためには色々と条件があるのだけれど、正規分布について言えば単に「微分したものを0とおく」操作をすればよい。ただし、このままでは扱いづらいことが多いので、通常は対数をとったもの（対数尤度関数）を最大化するようにする。実際にやってみよう。

$\displaystyle \frac{\partial}{\partial \mu} \log L(\mu, \sigma^2 | x_1, \cdots, x_N) \\ = \frac{\partial}{\partial \mu} \sum_{i=1}^{N} \log f(x_i | \mu, \sigma) \\ = \frac{\partial}{\partial \mu} \sum_{i=1}^{N} \log \left[ \frac{1}{\sqrt{2 \pi \sigma^2}} \exp \left\{ -\frac{(x_i - \mu)^2}{2 \sigma^2} \right\} \right] \\ = \frac{\partial}{\partial \mu} \left[ -\frac{N}{2} \log(2\pi) -\frac{N}{2} \log(\sigma^2) -\frac{1}{2\sigma^2} \sum_{i=1}^{N} (x_i - \mu)^2 \right] \\ = \frac{1}{\sigma^2} \sum_{i=1}^{N} (x_i - \mu) = 0$

平均 $\mu$ を推定するにはとりあえず分散 $\sigma^2$ は定数と考えてしまってよいので、最後の式を解くと

$\displaystyle \hat{\mu} = \frac{1}{N} \sum_{i=1}^{N}$

であり、尤度関数を最大にするような最適な平均パラメータの推定値は「手元にあるデータの平均値」、つまり標本平均ということになる（なお推定値であることを示すために「^」をつけている）。理論的にどのような推定がよいかはこれでわかったので、あとは実際のデータを当てはめれば日本人成人男性の平均身長の推定値は計算できる。
f:id:mstour:20201128210151j:plain

単回帰モデルにおける最尤法

では、単回帰モデルのパラメータ $\alpha, \beta$ を最尤法で推定するにはどうすればよいか？実は単回帰モデルにおいてもモデルを当てはめるべき目的変数 $y_1, \cdots, y_N$ は独立に正規分布に従うものと想定しているので、上で述べたことと同じような流れで推定できる。各 $y_i$ の平均は単回帰モデル $\alpha + \beta x_i$ で表され、共通の分散 $\sigma^2$ を持つとしているので、以下の尤度関数を最大にするような $\alpha, \beta, \sigma^2$ を求めればよい。

$\displaystyle L(\alpha, \beta, \sigma^2 | y_1, \cdots, y_N) \\ = \prod_{i=1}^{N} \frac{1}{\sqrt{2 \pi \sigma^2}} \exp \left\{ -\frac{(y_i - \alpha - \beta x_i)^2}{2 \sigma^2} \right\} \\ = \left( \frac{1}{\sqrt{2 \pi}} \right)^N \frac{1}{\sigma^N} \exp \left\{ -\frac{1}{2 \sigma^2} \sum_{i=1}^{N} (y_i - \alpha - \beta x_i)^2 \right\}$

実際にはこれの対数をとった対数尤度関数を最大化することになるが、最後の式をよくみると、指数expの中に

$\displaystyle \sum_{i=1}^{N} (y_i - \alpha - \beta x_i)^2$

という項がある。これは、データ $y_i$ と単回帰モデル $\alpha + \beta x_i$ との差の二乗の合計、つまり最小二乗法で小さくしようと目指す関数である。 $\alpha$ と $\beta$ に関係するのはこの部分だけなので、これを最小にすれば尤度関数は最大になる（マイナス符号がついているので）。つまり、最尤法で $\alpha$ と $\beta$ を求めるときにやっているのは最小二乗法と全く一緒である。
なお、 $\sigma^2$ の推定量を求めるには、対数尤度関数を $\sigma^2$ で偏微分して0とおけばよい。結果だけ示すと

$\displaystyle \hat{\sigma^2} = \frac{1}{N} \sum_{i=1}^{N} (y_i - \alpha - \beta x_i)^2$

となる。実際には $\sigma^2$ の不偏推定量（期待値をとると真の値に一致する推定量、要するに真の値から大きくはずれてはいないだろうという推定）は

$\displaystyle s^2 = \frac{1}{N-2} \sum_{i=1}^{N} (y_i - \alpha - \beta x_i)^2$

なので、前回の記事で述べたように最尤推定した $\hat{\sigma^2}$ には若干の偏りがあることになる。

まとめ

今回は最尤法による単回帰モデルの推定について、最尤法の大まかな説明を交えて述べた。長くなったのでここでいったん区切り、次回またRを使った実際の例なども紹介していこうと思う。
今回の参考文献は以下の通り。
[1] 鈴木武, 山田作太郎(1996), "数理統計学", 内田老鶴圃.
[2] Annette J. Dobson(2008), "一般化線形モデル入門", 共立出版.