はじめに
いわゆる「回帰分析」「回帰モデル」と呼ばれる統計方法のうち、最もシンプルな形式で多くの人に知られていると思われる「単回帰分析(Simple regression)」の話をしていこうと思う。
単回帰分析は、平面上のデータ点が散らばっているところへちょうどいい具合に直線をひくことになるので、直感的にとてもわかりやすい。しかしながら、その裏にはきちんとした数学的根拠があるのである。
今回はまず、どんなことをやっているのか、大雑把な説明をしていきたいと思う。
何をやっているのか
単回帰分析とは、端的に言うと、ある変数
の値を他の変数
の値を使って説明するような数式を立てることである（ただし、「にある定数を掛ける」と「それにある定数を足す」という条件を課す。の側にこのような制約を置くことはとても多いが、
を使うなど、例外ももちろんある）。説明される側の変数のことは目的変数・応答変数・反応変数・従属変数などなど、分野によっても人によっても色々な言い方がされる。ここでは目的変数と呼ぶことにする。を説明するための変数は説明変数と呼ばれる。
でを説明するとはどういうことか。次のようなデータがあるとする。
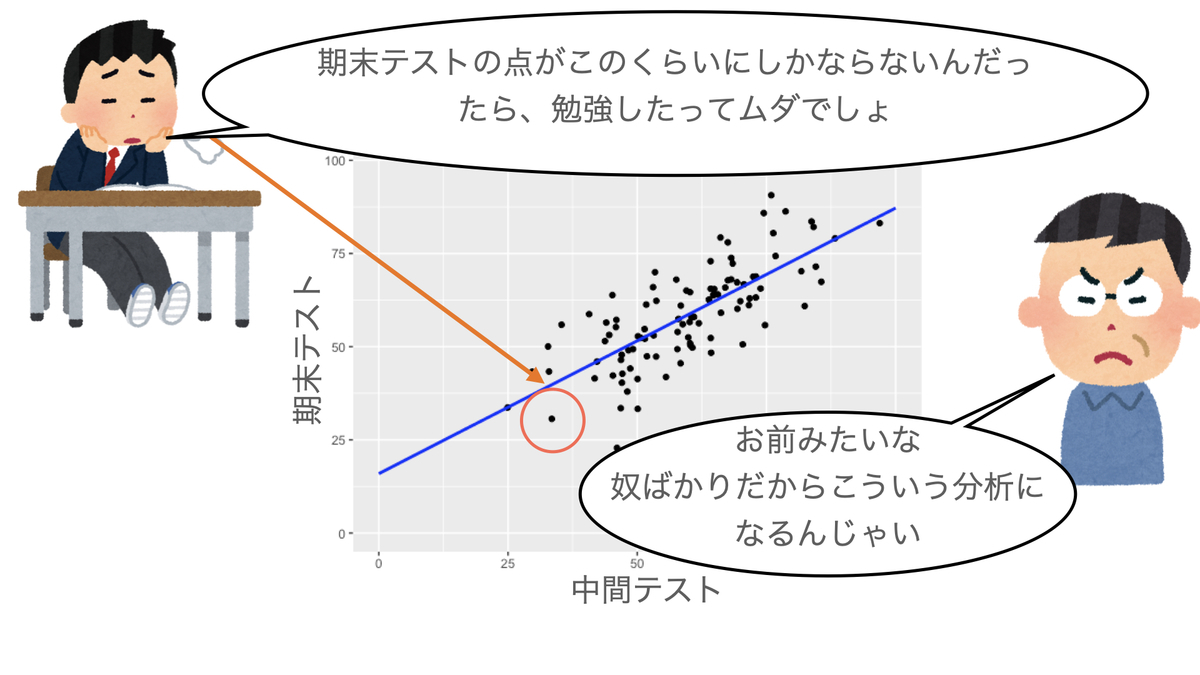
ここでを中間テストの得点、を期末テストの得点とすると、中間テストの成績がよかった（悪かった）人は期末テストでもよい（悪い）成績を収めたように見える。何だか、中間テストの得点で期末テストの得点を説明できそうな気がするのではないだろうか。
そのためには、期末テストの得点がどんな値でも、どうにかして中間テストの得点で説明できるような数式を作らないといけない。「にある定数を掛ける」と「それにある定数を足す」という縛りを考えると
という形の数式、つまり一次関数になる。なお、
ではなく
としているのは、正確には
にぴったり一致しないからである（後ほど説明）。
この状態では、
と
の値は具体的に決まっていない。これは、データに一番しっくりくるように決める必要がある。では、しっくりくるとはどういうことか。
この赤い直線は一次関数だが、データにしっくりきてはいないように見える。
どちらかと言えば、この緑の直線のほうがしっくりきていると言えるだろう。しかし、実際のどのデータ点からもちょっとだけズレてしまっている。直線で表現する以上、ズレを完全になくすことはできないので、せめてズレが最小になるような直線を選ぶことにする。すると、
と
の値が一つに決まるので、
を使って
を説明する数式が完成することになる。
なお数式の
という部分を見ると、
が直線の傾きを表していることがわかる。なので、
の値が決まれば、
が増えた時に
がどれだけ増えるかを知ることができる。
以上が、単回帰分析でやっていることの大まかな説明である。実際に計算すると次のようになる。
赤丸で囲っているところが、一番しっくりくる直線を選んだ結果決まった
と
の値である。
、
となっている。
選ばれた直線を元のデータ点に重ねると、次のようになった。
この直線によって、
と
との関係性をデータから構成することができた。しかしながら、得られた直線は実際の
の値ちょうどにはなっておらず、少なからずの「誤差」が残っている。今回は詳しく説明しないが、
で説明ができるのは
の真実の値のようなもの（正確には、期待値）だけであり、誤差について何らかの仮定を置かなければならないのである。
次回予告
次回は、数学的にきちんとした定義をし、単回帰分析のもう少しきちんとした意味を説明していきたい。
なお、中間テストの得点で期末テストの得点を統計的に説明できるからと言って、中間テストが悪い「ならば」期末テストも悪い、という因果関係が示されている訳ではない。これはなかなかうまく説明するのが難しい問題なのでまたいずれ書いてみたい。
今回の参考文献は以下の通り。
[1] 鈴木武, 山田作太郎(1996), "数理統計学", 内田老鶴圃.
[2] Annette J. Dobson(2008), "一般化線形モデル入門", 共立出版.
