線形モデルにおけるダミー変数 - 統計学入門一歩先へ

はじめに

前回紹介した「重回帰分析」は、統計モデルによって表現したい変数*1が正規分布に従うものと仮定した上で*2、その平均（期待値）を複数の要因（説明変数）によって説明する方法である。
mstour.hatenablog.com
前回見たように、重回帰分析モデルは、目的変数の平均を様々な要因の足し合わせで表現している。このようにモデルの構造が線形になっているような統計モデルは「線形モデル(Linear model)」と呼ばれることが多い。なお重回帰分析モデルは正規分布の仮定にちなみ「正規線形モデル(Normal linear model)」と呼ぶこともできる。

ところで、線形モデルは、目的変数の従う確率分布を正規分布に限定する必要はなく、「一般化線形モデル(Generalized linear model)」という形でさらなる拡張がなされている（例えばロジスティック回帰分析は、目的変数の分布を「ベルヌーイ分布」としたモデルである）。また、同じ個体から繰り返しデータを測定するような場合など、目的変数どうしに相関が生じるような状況に有効である「混合モデル(Mixed model)」も線形モデルの拡張と言える。

今後、こういった線形モデルの発展形を色々と紹介していきたいのだが、ここで「ダミー変数(Dummy variable)」なる概念について述べておきたい。

ダミー変数を用いた表現

ダミー変数が必要となるのは、線形モデルの説明変数としてカテゴリー型（離散型）変数が含まれるような場合である。

例えば、期末テストの点数を目的変数、その学期に参加した補習の種類（「放課後のみ」、「始業前＋放課後」、「なし」の3カテゴリー）を説明変数とした線形モデルを考えてみよう。
学生 $i$ の期末テストの点数を $y_i$ とすると、 $y_i$ は次のように表現できる：

$\displaystyle y_i = \mu + \alpha_j + \varepsilon_i \hspace{10pt} (i = 1, \cdots, N; j = 1, 2, 3) \hspace{20pt} (1)$

ここで $\mu$ は全体の平均を表し、 $\alpha_1, \alpha_2, \alpha_3$ はそれぞれ「放課後のみ補習を受けたグループ」、「始業前と放課後両方の補習を受けたグループ」、「補習を受けてないグループ」の全体平均との差を表している。 $\varepsilon_i$ は互いに独立に正規分布に従う誤差である。したがって、例えば学生番号1の人は補習を受けていなかったとすると、期末テストの点数は

$\displaystyle y_1 = \mu + \alpha_3 + \varepsilon_1$

という形でモデル化される。
f:id:mstour:20210107212944j:plain

さて、N人分の期末テストの点数に関するモデルをベクトルと行列を用いて表すことにする。「放課後のみ」「始業前＋放課後」「なし」のグループの人数をそれぞれ $n_1, n_2, n_3$ とする。目的変数ベクトルを

$\displaystyle \boldsymbol{y} = (y_1, \cdots, y_{n_1}, y_{n_1+1}, \cdots, y_{n_1+n_2}, y_{n_1+n_2+1}, \cdots, y_{N})^T$

パラメータベクトルを

$\displaystyle \boldsymbol{\beta} = (\mu, \alpha_1, \alpha_2, \alpha_3)^T$

両者を結びつける行列 $X$ （デザイン行列という）を

$\displaystyle X = \left( \begin{array}{cccc} 1 & 1 & 0 & 0 \\ \vdots & \vdots & \vdots & \vdots \\ 1 & 1 & 0 & 0 \\ 1 & 0 & 1 & 0 \\ \vdots & \vdots & \vdots & \vdots \\ 1 & 0 & 1 & 0 \\ 1 & 0 & 0 & 1 \\ \vdots & \vdots & \vdots & \vdots \\ 1 & 0 & 0 & 1 \\ \end{array} \right)$

と定義すると、モデル(1)は以下のように表現できる：

$\displaystyle \boldsymbol{y} = X \boldsymbol{\beta} + \boldsymbol{\varepsilon}.$

（なお、 $\boldsymbol{\varepsilon} = (\varepsilon_1, \cdots, \varepsilon_N)^T$ は誤差ベクトル）
この時、デザイン行列 $X$ の2〜4列目は、各学生がどのグループに所属しているかを0と1で表現している。2列目は「放課後のみ」、3列目は「始業前＋放課後」、4列目は「なし」に対応しており、値が0の場合はそのグループの所属ではなく、1の場合はそのグループに所属していることを示している。したがって、例えば2列目の値が1である学生のモデルにはパラメータ $\alpha_1$ が含まれることになる。
各列を説明変数と考えれば、この線形モデルには各学生がどのグループに所属するかを示す説明変数が3個あると考えることができる*3。このように定められた変数をダミー変数と呼ぶ。

ところが、最小二乗法によるパラメータベクトルの推定量は前回の記事で紹介した通り

$\displaystyle \hat{\boldsymbol{\beta}} = (X^T X)^{-1} X^T \boldsymbol{y}$

だが、実は上で定義したデザイン行列 $X$ ではパラメータベクトルの計算をすることができない*4。端的に言うと、パラメータの数が1つ余計だということである。
この問題を解決する方法の一つとして、カテゴリー型説明変数（ここの例では補習の種類）の「基準カテゴリー（例えば補習なし）」の平均を $\mu$ とし、基準カテゴリーとその他のカテゴリーとの差を $\alpha_1, \alpha_2$ と定義する方法がある。こうすることで、デザイン行列 $X$ の4列目が消え、先ほどの問題は解消する。
f:id:mstour:20210107213013j:plain

重回帰モデルと同様の表現

モデル(1)は、一般的な重回帰モデルの形式で書くこともできる。

$\displaystyle y_i = \beta_0 + \beta_1 x_{i1} + \beta_2 x_{i2} + \beta_3 x_{i3} + \varepsilon_i \hspace{10pt} (i = 1, \cdots, N) \hspace{20pt} (2)$

ここで $x_{ij}(j = 1, 2, 3)$ はそれぞれ、学生 $i$ がグループ $j$ に所属していれば1を、そうでなければ0になるような変数としている。したがって、 $\beta_1, \beta_2, \beta_3$ はそれぞれモデル(1)の $\alpha_1, \alpha_2, \alpha_3$ に、 $\beta_0$ は $\mu$ に対応している。
ただし、ここでも先ほど述べたようにパラメータベクトルの推定計算ができない問題が生じるので、基準カテゴリーを決める必要がある。

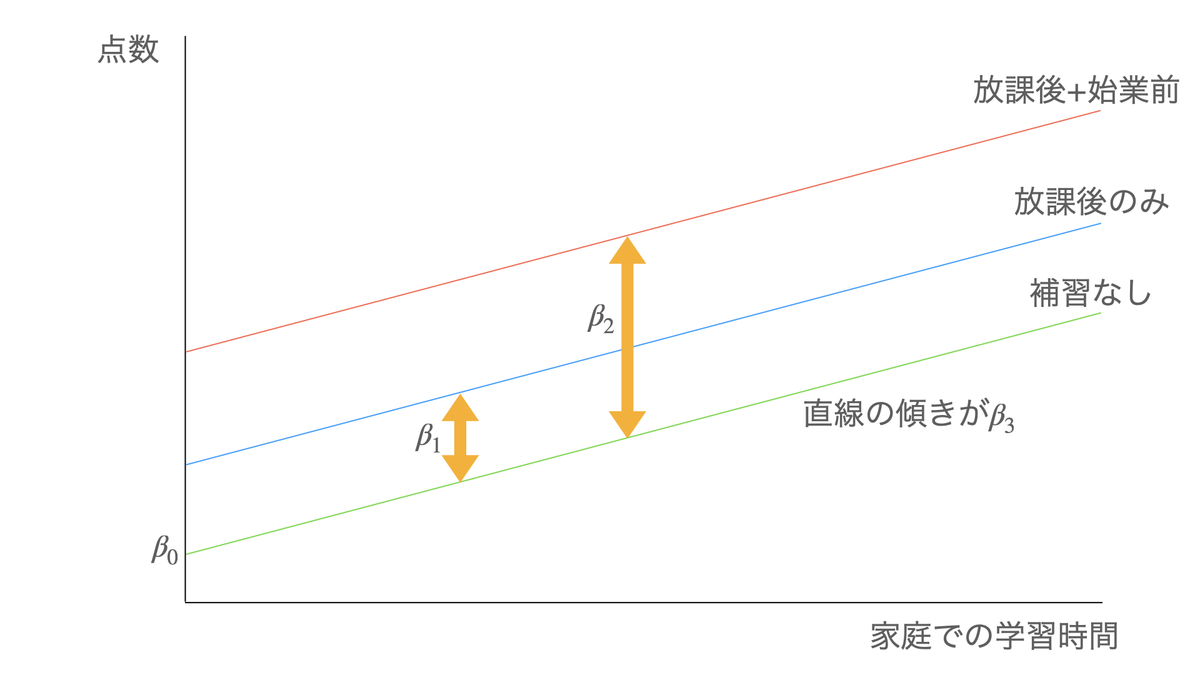
基準カテゴリーを補習なしのグループとすると、モデルは以下のようにすればよい。

$\displaystyle y_i = \beta_0 + \beta_1 x_{i1} + \beta_2 x_{i2} + \varepsilon_i \hspace{10pt} (i = 1, \cdots, N) \hspace{20pt} (3)$

こうすると、補習なしのグループの学生は $x_{i1}, x_{i2}$ の値がともに0なので、切片 $\beta_0$ が補習なしのグループの平均に相当する。そして $\beta_1$ が放課後のみグループの（補習なしに対する上乗せの）効果を、 $\beta_2$ が始業前+放課後グループの（補習なしに対する上乗せの）効果をそれぞれ表すことになる。
f:id:mstour:20210107213033j:plain

連続型とカテゴリー型の説明変数を混在させることも可能で、例えば上記モデル(3)に家庭での学習時間 $x_{i3}$ を説明変数として追加すると

$\displaystyle y_i = \beta_0 + \beta_1 x_{i1} + \beta_2 x_{i2} + \beta_3 x_{i3} + \varepsilon_i \hspace{10pt} (i = 1, \cdots, N) \hspace{20pt}$

となる*5。

なおダミー変数を使用する場合、データの形は例えば以下の図のようになる。
f:id:mstour:20210106201944j:plain
またダミー変数を説明変数に含めた重回帰分析を行うと、例えば次のような結果が得られる。各ダミー変数の係数の推定値が、基準カテゴリー（ここでは補習なし）と各カテゴリーとの差である。
f:id:mstour:20210106202205j:plain

まとめ

今回は、線形モデルの説明変数にカテゴリー型の変数を含める場合に用いられる、ダミー変数と呼ばれる概念について説明した。
今回は以下の文献を参考にした。
[1] Annette J. Dobson(2008), "一般化線形モデル入門", 共立出版.
[2] H.Brown, R.Prescott(2015), "Applied Mixed Models in Medicine", Wiley.

*1:目的変数、結果変数など様々な言い方があるが、本ブログでは特別な事情がない限り「目的変数」という表現で統一したいと思う。

*2:「誤差」が正規分布に従うと説明される場合もあるが、どちらでも同じことなのでここでは目的変数自体の分布という言い方をすることにする。

*3:なお、1列目は切片に相当する。

*4: $X$ の全ての列が1次独立でない場合、パラメータ推定ができないことが知られている。上記の例では、2〜4列目を合計すると1列目に等しくなることから、1次独立性を満たさないこととなる。

*5:共分散分析(Analysis of covariance)はこのような表現になる。