単回帰分析(2)モデルの定式化と最小二乗法

はじめに

前回は単回帰分析の大まかなイメージを紹介した。今回は数学的にもう少し整理したいと思う。
最初に言葉でざっくりとまとめると、説明変数 $x$ で目的変数 $y$ を表現する単回帰分析とは、

目的変数 $y$ は正規分布に従うと仮定し、
その期待値 $E[ y | x ]$ を推定する

という方法である。なお、 $E[ y | x ]$ は正確には $x$ による $y$ の条件付き期待値であり、すでに観測されている $x$ の値によって $y$ の真の状態を推定することから「 $x$ による条件付き」という形になる。よって、 $y$ は確率的にばらつくことを前提としている一方、 $x$ は固定した値と考える（ $x$ もばらつきを持っていると想定する方法も当然ある）。

単回帰分析モデルの定式化

前回、単回帰分析は、データに上手く当てはまるような直線を引いていると説明した。つまり、 $x$ によって説明される $y$ の真の状態（期待値）は、 $x$ の一次関数であると仮定している：

$\displaystyle E[ y | x ] = \alpha + \beta x$

ところで、 $y$ は正規分布に従うと仮定しているので、期待値 $E[ y | x ]$ の周りでばらつくと考えていることになる。そのばらつきの部分を「誤差項」といい、 $\varepsilon$ で表す。したがって、 $y$ は期待値に誤差を加えて

$\displaystyle y = \alpha + \beta x + \varepsilon$

という構造になっている（と想定している。もちろんこの表現が必ずしも現実を上手く説明できるかは分からない）。この数式を単回帰分析モデルと言う（一般に、統計学的な方法によってデータの振る舞いを説明する時、そのような数式表現を統計モデルと言うことが多い）。
さて、今得られているデータとして、 $x$ と $y$ の組が $N$ 組あるものとする。単回帰モデルを今得られているすべてのデータに当てはめることを考えると、 $i$ 番目の組は以下のように表される。

$\displaystyle y_i = \alpha + \beta x_i + \varepsilon_i$

これで、あとは $\alpha$ と $\beta$ をデータから推定すればよい。また、それぞれの $y_i$ のばらつき（分散） $\sigma^2$ も通常は分からないので、データから推測することになる。これらを推定するための方法として、最小二乗法(Least squares method)と最尤法(Maximum likelihood method)という方法が代表的である。今回は最小二乗法による推定を説明したいと思う。単回帰モデルの場合（正確に言えば、目的変数の分布が正規分布の場合） $\alpha$ と $\beta$ の推定結果は同じになる。
なお、各 $y_i$ どうしは独立であることを仮定している。例えば別々の個人から得られたデータであれば通常は独立と考えても問題はないが、同じ個人から何度も測定したデータであればそういう訳にはいかない。この場合にはもっと込み入った方法が必要になる。

最小二乗法

では、最小二乗法によって未知の値 $\alpha, \beta, \sigma^2$ をデータから推測する方法を述べる。
最小二乗法とは、まさに前回説明したイメージの通り、データとのズレを最小にするようにして最適な統計モデルを決定する方法である。
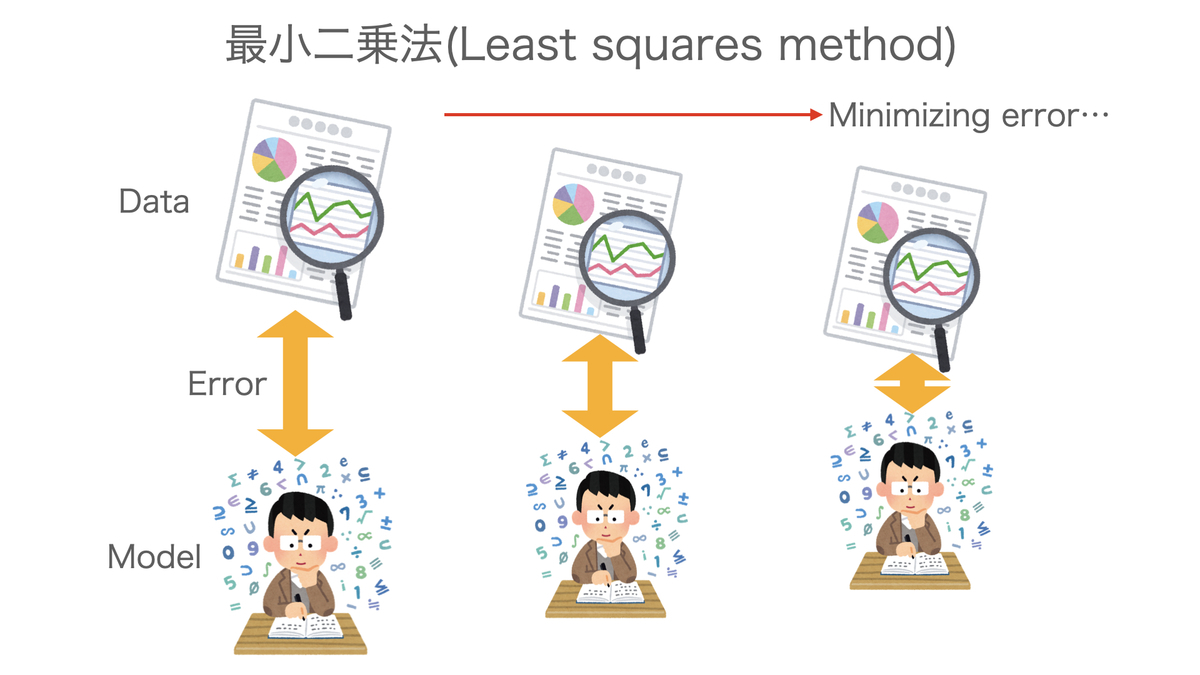
f:id:mstour:20201121054643j:plain
正確には、次のように実際のデータ $y_i$ とモデルで推定される期待値 $E[ y_i | x_i ] = \alpha + \beta x_i$ との差である偏差(Deviation)を二乗したものの合計

$\displaystyle Q(\alpha, \beta) = \sum_{i=1}^{N} \left\{ y_i - (\alpha + \beta x_i) \right\}^2$

を最小にすることを考える。この合計を偏差平方和(Sum of squared deviation)という。
$Q(\alpha, \beta)$ は $\alpha$ と $\beta$ それぞれの二次関数になっているので、最小にするような $\alpha$ と $\beta$ は「微分して0とおく」という操作をすれば計算できる（傾きがゼロになる点が最小になる）。

$\displaystyle \frac{\partial Q(\alpha, \beta)}{\partial \alpha} = 0, \hspace{20pt} \frac{\partial Q(\alpha, \beta)}{\partial \beta} = 0$

これを整理すると、正規方程式と呼ばれる連立方程式が得られる。

$\displaystyle \alpha N + \beta \sum_{i=1}^{N} x_i = \sum_{i=1}^{N} y_i, \hspace{20pt} \alpha \sum_{i=1}^{N} x_i + \beta \sum_{i=1}^{N} x_i^2 = \sum_{i=1}^{N} x_i y_i$

まず $\beta$ の方から解いていこう。 $\beta$ の最適解 $\hat{\beta}$ は

$\displaystyle \hat{\beta} = \frac{\sum_{i=1}^{N} (x_i - \overline{x})(y_i - \overline{y})}{\sum_{i=1}^{N} (y_i - \overline{y})^2}$

となる。ただし $\overline{x}, \overline{y}$ はそれぞれ $x, y$ の標本平均である。これは、 $x$ と $y$ の標本共分散を $y$ の標本分散で割ったものに等しい。
この結果を得た上で $\alpha$ の最適解 $\hat{\alpha}$ を求めると

$\displaystyle \hat{\alpha} = \overline{y} - \hat{\beta} \overline{x}$

となる。あとは、データから $\hat{\alpha}, \hat{\beta}$ を算出することができる。
これらの最適解（推定量）は、期待値をとると（つまり、真の値は） $\alpha, \beta$ に一致する。つまり、最小二乗法で計算すると、未知の $\alpha, \beta$ は偏りなく推定ができることになる。このような推定量を不偏推定量という。
最後にばらつきのパラメータ $\sigma^2$ は、推定した $\hat{\alpha}, \hat{\beta}$ を使って次のように推定できる。これも期待値が $\sigma^2$ に一致する不偏推定量である。

$\displaystyle \hat{\sigma^2} = \frac{1}{N-2} \sum_{i=1}^{N} \left\{ y_i - (\hat{\alpha} + \hat{\beta} x_i) \right\}^2$

なお、最尤法で $\alpha, \beta, \sigma^2$ を推定する場合、 $\sigma^2$ の推定量は不偏ではないことが知られている。しかし、違いは $\frac{N-2}{N}$ なので、サンプル数が大きければそこまでの違いはない。

まとめ

単回帰分析のモデルを数学的に定義し、推定方法の一つである最小二乗法について説明した。最小二乗法は「データとモデルとのズレ」を小さくするという単純な問題に帰着するので確率分布のことが表に出てこないが、もっと様々な種類のデータ（二値のデータやカウントデータなど）をモデルで表現するためには、適切な確率分布を考えていく必要があり、そのような場合には最尤法が出番となる。

今回の参考文献は以下の通り。
[1] 鈴木武, 山田作太郎(1996), "数理統計学", 内田老鶴圃.
[2] Annette J. Dobson(2008), "一般化線形モデル入門", 共立出版.