反復測定データのモデリング：(2)混合モデル

はじめに

前回は反復測定データの特徴である、同じ個人や集団から得られたデータの相関を考慮したモデリングを行うための一つの方法として、Covariance pattern modelを紹介した。Covariance pattern modelは、全ての目的変数をまとめて多変量正規分布に従う変数と考え、相関の構造も含めて線形モデルとして表現する方法と言える。

今回は、反復測定データに対するモデリングとして代表的なもう一つの方法である、混合モデル(Mixed model)を紹介する。混合モデルも、重回帰分析に代表される線形モデル（つまり、いくつかの説明変数が目的変数へ与える影響を評価する、あるいは説明変数を使って将来の目的変数の予測を行う）を拡張したものの一つである。
なお、今回もCovariance pattern modelと同様に確率分布としては正規分布のみを考えることにする*1。目的変数の従う分布として正規分布以外を考えたい場合には、一般化線形モデルを拡張した「一般化線形混合モデル(Generalized linear mixed model; GLMM)」という方法がある。

混合モデルも結果的には目的変数の分布として多変量正規分布を考えることになるわけだが、Covariance pattern modelと異なり、反復測定された目的変数1つ1つを明示的にモデリングしていく。
例えばN人の個人からそれぞれT回の測定データを得たものとする。この時、まず研究への参加者としてN人の個人が（大きな母集団からランダムに）選ばれていることを反映するため、N人の個人ごとの測定値の違いをモデルの中に取り込む。これは後で述べるように変量効果、あるいはランダム効果(Random effect)と呼ばれる。その次に、各個人のT回の測定に伴うばらつきを誤差としてモデルに取り込む。
また全体集団の中のM個の小集団（クラスター）から反復測定データを得るような場合、まずM個の小集団が（全体集団からランダムに）選ばれていることを反映するために同じくランダム効果をモデルに含める。続いて、小集団内でのばらつきを誤差としてモデルに含める。
このように反復測定データが得られた状況を踏まえたモデリングを行うことによって、データ間の相関を考慮した評価を行うことができるようになる。

混合とは？

モデルの詳細に入る前に、「混合」とはどういうことかを確認する。
といってもそう難しい話ではなくて、線形モデルを構成する（つまり、目的変数の平均を構成する）成分が「固定効果(Fixed effect)」と「ランダム効果(Random effect)」の二種類を混合したものになっている、ということを意味する。

固定効果とは？

固定効果とは、線形モデルを構成する成分のうち、ランダムにばらつかずに固定された値をとるもののことをいう。例えば以下の重回帰モデル

$\displaystyle y_i = \beta_0 + \beta_1 x_{i1} + \beta_2 x_{i2} + \varepsilon_i$

のパラメータ $\beta_0, \beta_1, \beta_2$ はいずれも確率的にばらつくことを想定しておらず、ある決められた値をとると考えている。そのため、データから最もそれらしいと思われる値を直接推定することができる*2。

上記のような重回帰モデルや一般化線形モデルは、通常は確率的に変動するものは誤差 $\varepsilon_i$ だけとされ、目的変数の平均の構成要素としては固定効果だけを含む。このようなモデルは固定効果モデルと言われることもある。

ランダム効果とは？

ただし「はじめに」で述べたように、反復測定データにおいてははそれらがランダムに選ばれた個人や集団から得られたものであることを考慮するのが望ましい。そのため、個人（あるいは集団）ごとの目的変数の値の系統的な違いをモデルに取り込みたい。
そこで、線形モデルの構成要素に、データが得られた個人ごとの違いを表す項を追加する。追加された項は、それぞれの個人がより大きな集団からランダムに選ばれたことを反映するため、ばらつきを持つ確率変数として考える。これをランダム効果と呼んでいる。

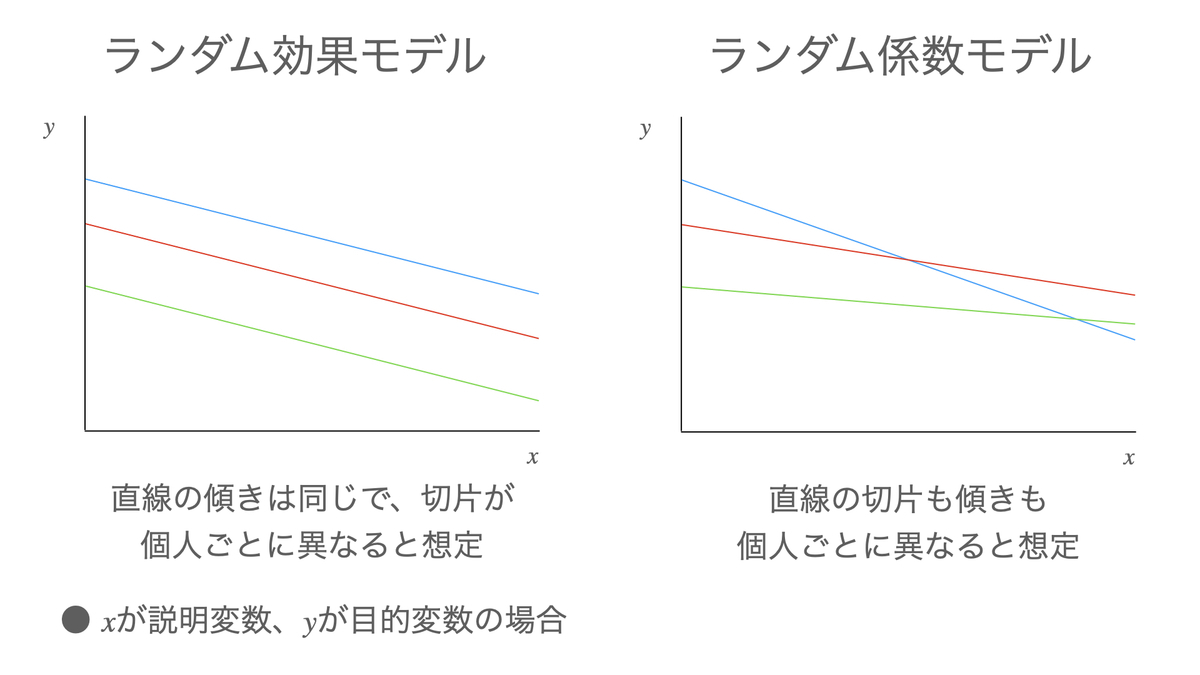
最も単純な形は、目的変数の平均的な水準に個人差があることを表現したいような場合で、単純に固定効果モデルにランダム効果を足し算する。このようなモデルは「ランダム効果モデル(Random effects model)」や「ランダム切片モデル(Random intercept model)」と表現されることがある（以下では「ランダム効果モデル」と言うことにする）。このモデルについては後ほど詳しく述べる。
また、ある説明変数の係数（つまり回帰直線の傾き）にランダム効果を追加することもできる。このようなモデルは「ランダム係数モデル(Random coefficients model)」と呼んでランダム効果モデルとは区別されることが多い。このモデルも合わせて説明すると長くなるので、また回を改めて述べることにする。
f:id:mstour:20210214203400j:plain

モデルの定式化

ランダム効果モデルについて、数式で説明する。

例として、N人の個人からそれぞれT回測定した反復測定データのモデリングを考える。個人 $i$ の $j$ 回目の測定値を $y_{ij}$ とする。
話を単純にするために、各 $y_{ij}$ を表現するモデルに説明変数は何も含めず、固定効果としては全体平均 $\mu$ だけを用いるものとする。
いま、異なる個人からそれぞれT回の測定がなされていることを反映するため、個人 $i$ の全体平均からの差（個人差）をランダム効果 $r_i$ で表す。そして、同じ個人内での測定値の誤差を $\varepsilon_{ij}$ とすると、 $y_{ij}$ は以下のランダム効果モデルで表現できる：

$\displaystyle y_{ij} = \mu + r_i + \varepsilon_{ij}$

ただし、ランダム効果 $r_i(i = 1, \cdots, N)$ は互いに独立に正規分布 $N(0, \sigma^2_r)$ に従い、誤差 $\varepsilon_{ij}(i = 1, \cdots, N; j = 1, \cdots, T)$ も互いに独立に正規分布 $N(0, \sigma^2_{\varepsilon})$ に従うものと仮定する。さらに全ての $r_i$ と $\varepsilon_{ij}$ のペアも独立とする。
このモデルは、N人の全データの平均が $\mu$ 、個人 $i$ の平均が $\mu + r_i$ であり、個人 $i$ の各測定値には $\varepsilon_{ij}$ の誤差が生じていることを示している。
f:id:mstour:20210214203420j:plain

このようにモデル化した場合の $y_{ij}$ の分散と共分散を見てみよう。
分散は、ランダム効果と誤差との独立性より全ての $i, j$ について

$\displaystyle V(y_{ij}) = V(r_i) + V(\varepsilon_{ij}) = \sigma^2_r + \sigma^2_{\varepsilon}$

共分散は、同じ個人どうしの測定値については

$\displaystyle Cov(y_{ij}, y_{iq}) = Cov(r_i + \varepsilon_{ij}, r_i + \varepsilon_{iq}) = V(r_i) = \sigma^2_r$

異なる個人どうしの測定値では

$\displaystyle Cov(y_{ij}, y_{pq}) = Cov(r_i + \varepsilon_{ij}, r_p + \varepsilon_{pq}) = Cov(r_i, r_p) = 0$

となる。したがって、同じ個人内のデータどうしについては相関があることが表現されている*3。

最後に、ランダム効果モデルだけでなくランダム係数モデルも含めた混合モデルの一般的な表現をまとめる。
前回のCovariance pattern modelでの説明と同様に、反復測定データを全て並べたベクトルを $\boldsymbol{y}$ 、誤差を全て並べたベクトルを $\boldsymbol{\varepsilon}$ とする。
モデルに含まれる全ての固定効果を $\boldsymbol{\beta}$ 、全てのランダム効果を $\boldsymbol{u}$ とすると、混合モデルは以下のように表現することができる。

$\displaystyle \boldsymbol{y} = X \boldsymbol{\beta} + Z \boldsymbol{u} + \boldsymbol{\varepsilon}$

なおランダム効果と誤差はそれぞれ多変量正規分布 $N(\boldsymbol{0}, G)$ と $N(\boldsymbol{0}, R)$ に従うものと想定する。
$X$ は固定効果に関するデザイン行列で、通常の線形モデルと同様に説明変数から構成される。
さらに $Z$ はランダム効果に関するデザイン行列であり、ランダム効果をモデルのどこに含めるかの情報を持っている。例えばこのセクションの前半で説明したランダム効果モデルの場合、ランダム効果は1個だけが足し算で加わっているので、 $Z$ は全ての要素が1のベクトルとなる。ランダム係数モデルの場合には、ランダム効果が入る（つまり、係数に個人差を考える）説明変数が $Z$ の要素に追加される。

目的変数ベクトル $\boldsymbol{y}$ の平均は、Covariance pattern modelと同様に

$\displaystyle \boldsymbol{\mu} = X \boldsymbol{\beta}$

であり、分散共分散行列は

$\displaystyle V(\boldsymbol{y}) = Z G Z^T + R$

となる*4。

固定効果 $\boldsymbol{\beta}$ の推定もCovariance pattern modelと同じく最尤法によって行うことができ、結果は以下の通りとなる。

$\displaystyle \hat{\boldsymbol{\beta}} = (X^T V^{-1} X)^{-1} X^T V^{-1} \boldsymbol{y}$

まとめ

反復測定データの（正規分布を想定した）モデリング方法の1つである混合モデルの概要を紹介した。
混合モデルでは、通常の線形モデルでパラメータとして考える「固定効果」に加えて個人差を表すための「ランダム効果」を導入することにより、同じ個人から繰り返しデータが測定されていることを反映することができる。

なお、実際の応用ではグループ間の平均に統計的に有意な差があるかどうかとか、ある説明変数が目的変数に与える影響の信頼区間などを見たいことが多くあり、そのためには固定効果の推定量 $\hat{\boldsymbol{\beta}}$ の分散を計算する必要がある。しかしながら、分散の計算には少しやっかいな問題が絡んでおり、なかなか複雑である。また次回以降に説明してみたい。

今回は以下の文献を参考にした。
[1] Annette J. Dobson(2008), "一般化線形モデル入門", 共立出版.
[2] Brown and Prescott(2015), "Applied Mixed Models in Medicine", Wiley.

*1:このような場合を参考文献[2]では「正規混合モデル(Normal mixed model)」と呼んでいる

*2:ややこしいが、パラメータの「真の値」についての話であることに注意して欲しい。最尤法や最小二乗法で求めるパラメータの「推定量」はデータをとるたびに確率的にばらつく。

*3: $y_{ij}$ と $y_{pq}$ との相関係数は共分散をそれぞれの分散の平方根で割ったものなので、 $\frac{\sigma^2_r}{\sigma^2_r + \sigma^2_{\varepsilon}}$ となる。これは「全体のばらつきのうち、個人差に起因する部分の割合」を示しており、級内相関係数(Intraclass Correlation Coefficient; ICC)と呼ばれることが多い。

*4:通常、混合モデルではランダム効果と誤差の分散共分散行列 $G, R$ のそれぞれの要素を推定する。一方、 $\boldsymbol{y}$ の（ランダム効果に関して周辺化した）分散共分散行列を $Z G Z^T + R = V$ のように $V$ としてひとまとめにすると、Covariance pattern modelと同様のモデルになる。医学研究の分野ではこのようなモデルをMMRM(Mixed Model for Repeated Measures)と呼ぶことがある。