ギブス・サンプリングの実装練習：(1)ランダム効果モデル

2021/11/14 赤字部分を追記

はじめに

このブログではあまりベイズ統計の話題は書いてこなかったのですが、やはりこれからの時代それではいかんということで、こんなことをやってみることにします。

ベイズモデルにおいてパラメータの事後分布を推定する際にはMCMC法がよく使われますが、代表的なアルゴリズムの一つにギブス・サンプリング(Gibbs sampling)というものがあります。
この方法はざっくり言うと、推定したいパラメータ一つ一つの「完全条件付き分布(Full conditional distribution)」*1を導出し、そこから順繰りにサンプリングを繰り返せば各パラメータの事後分布の推定ができる、というものです。
f:id:mstour:20211101190906j:plain

今回はギブス・サンプリングの理論的な説明ではなく、具体的な計算をRで実行するためのコードを書いてみることにします。
今回の題材は、Gelfandらの1990年の論文（参考文献[1]）にて解説されている以下のランダム効果モデルです。

$\displaystyle Y_{ij} = \theta_i + e_{ij} \hspace{10pt} (i = 1, \cdots, K; \hspace{5pt} j = 1, \cdots, J)$

ただし $\theta_i$ は互いに独立に正規分布 $N(\mu, \sigma^2_{\theta})$ に、 $e_{ij}$ は互いに独立に正規分布 $N(0, \sigma^2_e)$ に従うものとし、 $\theta_i, e_{ij}$ どうしも互いに独立とします。
ここでは、 $Y_{ij}, e_{ij}$ はそれぞれ個人 $i$ の $j$ 番目の測定値とランダムな誤差を表すものとし、 $\theta_i$ は個人 $i$ に特有の個人差を表すランダム効果と考えます*2。

またパラメータ $\mu, \sigma^2_{\theta}, \sigma^2_e$ は互いに独立に以下の事前分布に従うものとします（ $IG$ は「逆ガンマ分布」を表します）：

$\displaystyle p(\mu) = N(\mu_0, \sigma^2_0), \\ p(\sigma^2_{\theta}) = IG(a_1, b_1), \\ p(\sigma^2_e) = IG(a_2, b_2)$

ただし、上記の事前分布のパラメータ $\mu_0, \sigma^2_0, a_1, b_1, a_2, b_2$ （ハイパーパラメータと言います）は全て既知の値とします*3。
これらは共役事前分布と呼ばれており、このように設定することで各パラメータの事後分布*4は事前分布と同じ種類の分布になることが知られています。したがって手計算によって事後分布を具体的に導出することができます。
もちろん実用では共役事前分布を用いる必要はないのですが（むしろ現実に即したモデリングには適さないことがあるかもしれません）、事後分布が基本的な確率分布で書き下せるため、今回やろうとしているギブス・サンプリングには非常に都合が良いわけです。

さて、データ $Y = (Y_{11}, \cdots, Y_{KJ})$ が得られたと想定して、パラメータ $\mu, \sigma^2_{\theta}, \sigma^2_e$ の事後分布の推定をギブス・サンプリングを用いて行ってみたいと思います。
サンプリングを行うためには、パラメータ $\mu, \sigma^2_{\theta}, \sigma^2_e$ の他に、ランダム効果 $\theta = (\theta_1, \cdots, \theta_K)$ の完全条件付き分布の特定が必要です。
まずはこれらの完全条件付き分布を導出し、それを用いたサンプリングアルゴリズムを示します。
その後、Rでの実装例と結果を紹介していきます。

完全条件付き分布の導出

今回の例では、 $\mu, \sigma^2_{\theta}, \sigma^2_e, \theta$ の完全条件付き分布は全てよく知られた確率分布になることを手計算で確かめることができます。少し大変ですが、一つずつやっていきます。

$\mu$ の完全条件付き分布

まずは $\mu$ の完全条件付き分布、つまり他の変数 $\sigma^2_{\theta}, \sigma^2_e, \theta$ で条件付けた分布を導出します。なお、得られたデータ $Y$ を反映した事後分布を推定するためには、 $Y$ での条件付けも必要です。
条件付き確率の定義を用いると、次のように変形できます。なお記号 $\propto$ は左辺と右辺が比例関係にあることを表します*5。

$\displaystyle p(\mu | Y, \theta, \sigma^2_{\theta}, \sigma^2_e) \\ \propto p(\mu, Y | \theta, \sigma^2_{\theta}, \sigma^2_e) \\ = p(Y | \mu, \theta, \sigma^2_{\theta}, \sigma^2_e) p(\mu | \theta, \sigma^2_{\theta}, \sigma^2_e) \\ \propto p(Y | \theta, \sigma^2_e) p(\theta | \mu, \sigma^2_{\theta}) p(\mu)$

最後の式変形には少し注意が必要です。 $p(\mu | \theta, \sigma^2_{\theta}, \sigma^2_e)$ を条件付き確率の定義にしたがって変形してみます。

$\displaystyle p(\mu | \theta, \sigma^2_{\theta}, \sigma^2_e) \\ = \frac{p(\mu, \theta | \sigma^2_{\theta}, \sigma^2_e)}{p(\theta | \sigma^2_{\theta}, \sigma^2_e)} \\ = \frac{p(\theta | \mu, \sigma^2_{\theta}, \sigma^2_e) p(\mu | \sigma^2_{\theta}, \sigma^2_e)}{p(\theta | \sigma^2_{\theta}, \sigma^2_e)} \\ = \frac{p(\theta | \mu, \sigma^2_{\theta}) p(\mu)}{p(\theta | \sigma^2_{\theta})}$

なお最後の等式に移る際に、条件部分にある無関係なパラメータを削除しました。
モデルの設定から、 $\theta$ の値は、分布の平均パラメータ $\mu$ と分散パラメータ $\sigma^2_{\theta}$ の両方に依存します。したがって、分子の $p(\theta | \mu, \sigma^2_{\theta})$ と分母の $p(\theta | \sigma^2_{\theta})$ が必ずしも一致しないため、完全条件付き分布には $p(\theta | \mu, \sigma^2_{\theta}) p(\mu)$ の2つの確率分布が残ることになります。もしも $\theta$ が $\mu$ に依存しない構造になっていれば、残るのは $p(\mu)$ だけになります。

さて、完全条件付き分布は3つの確率分布の積の形になっていることがわかりましたが、モデルの設定より、これらは全て正規分布です。この時、最終的に得られる分布も正規分布になります。
具体的に式を変形していくと、以下のようになります。

$\displaystyle p(\mu | Y, \theta, \sigma^2_{\theta}, \sigma^2_e) \\ \propto p(Y | \theta, \sigma^2_e) p(\theta | \mu, \sigma^2_{\theta}) p(\mu) \\ = \left[ \prod_{i=1}^{K} \prod_{j=1}^{J} \frac{1}{\sqrt{2 \pi \sigma^2_e}} \exp \left\{ -\frac{1}{2 \sigma^2_e} (Y_{ij} - \theta_i)^2 \right\} \right] \left[ \prod_{i=1}^{K} \frac{1}{\sqrt{2 \pi \sigma^2_{\theta}}} \exp \left\{ - \frac{1}{2 \sigma^2_{\theta}} (\theta_i - \mu)^2 \right\} \right] \left[ \frac{1}{\sqrt{2 \pi \sigma^2_0}} \exp \left\{ - \frac{1}{2 \sigma^2_0} (\mu - \mu_0)^2 \right\} \right] \\ \propto \exp \left\{ \frac{1}{\sigma^2_{\theta}} \sum_{i=1}^{K}(\theta_i^2 - 2 \theta_i \mu + \mu^2) + \frac{1}{\sigma_0} (\mu^2 - 2 \mu_0 \mu + \mu_0^2) \right\} \\ \propto \exp \left\{ \left( \frac{K}{\sigma^2_{\theta}} + \frac{1}{\sigma^2_0} \right) \mu^2 - 2 \left( \frac{\sum_{i=1}^{K} \theta_i}{\sigma^2_{\theta}} + \frac{\mu_0}{\sigma^2_0} \right) \mu \right\}$

確率分布を上記のような2次式の指数関数の形で表すことができるとき、その確率分布は正規分布であることが知られており、平均と分散はそれぞれ1次および2次の項の係数を使って表せます。高校の時？に学んだように $\mu^2$ の係数 $\left( \frac{K}{\sigma^2_{\theta}} + \frac{1}{\sigma^2_0} \right)$ をくくり出して整理すれば、正規分布でよく見慣れた形になるのが確かめられます。
結果、完全条件付き分布は $N\left( \frac{\sigma^2_{\theta} \mu_0 + \sigma^2_0 \sum_{i=1}^{K} \theta_i}{\sigma^2_{\theta} + K \sigma^2_0}, \frac{\sigma^2_{\theta} \sigma^2_0}{\sigma^2_{\theta} + K \sigma^2_0} \right)$ となります。

$\sigma^2_{\theta}$ の完全条件付き分布

同様にして数式展開していきましょう。
$\sigma^2_{\theta}$ の事前分布 $p( \sigma_{\theta}^{2} )$ はパラメータ $a_1, b_1$ の逆ガンマ分布としていました。

$\displaystyle p( \sigma_{\theta}^{2} | Y, \mu, \theta, \sigma_{e^{2}} ) \\ \propto p( \sigma_{\theta}^{2}, Y | \mu, \theta, \sigma_{e}^{2} ) \\ \propto p( Y | \theta, \sigma^2_e) p( \theta | \mu, \sigma_{\theta}^{2} ) p( \sigma_{\theta}^{2} ) \\ = \left[ \prod_{i=1}^{K} \prod_{j=1}^{J} \frac{1}{\sqrt{2 \pi \sigma_{e}^{2} }} \exp \left\{ - \frac{1}{2 \sigma_{e}^{2}} \left( Y_{i j} - \theta_{i} \right)^{2} \right\} \right] \left[ \prod_{i=1}^{K} \frac{1}{\sqrt{2 \pi \sigma_{\theta}^{2} }} \exp \left\{ - \frac{1}{2 \sigma_{\theta}^{2}} \left( \theta_{i} - \mu \right)^{2} \right\} \right] \frac{b_{1}^{a_{1}}}{\Gamma \left(a_{1} \right)} \left( \frac{1}{\sigma_{\theta}^{2}} \right)^{a_{1}+1} \exp \left( -\frac{b_{1}}{\sigma_{\theta}^{2}} \right) \\ \propto \left( \frac{1}{\sigma_{\theta}^{2}} \right)^{a_{1}+\frac{K}{2}+1} \exp \left\{ -\frac{1}{\sigma_{\theta}^{2}} \left( \frac{1}{2} \sum_{i=1}^{K} \left( \theta_{i} - \mu \right)^{2} +b_{1} \right) \right\}$

最後の等式の形から、完全条件付き分布はパラメータ $a_1 + \frac{K}{2}, b_1 + \frac{\sum_{i=1}^{K} (\theta_i - \mu)^2}{2}$ の逆ガンマ分布であることがわかります。

$\sigma^2_e$ の完全条件付き分布

$\sigma^2_{\theta}$ の時とほぼ同様です。

$\displaystyle p\left(\sigma_{e}^{2} \mid Y, \mu, \theta, \sigma_{\theta}^{2}\right) \\ \propto p\left(\sigma_{e}^{2}, Y \mid \mu, \theta, \sigma_{\theta}^{2}\right) \\ \propto p(Y \mid \theta, \sigma^2_e) p\left(\sigma_{e}^{2}\right) \\ = \left[\prod_{i=1}^{K} \prod_{j=1}^{J} \frac{1}{\sqrt{2 \pi \sigma_{e}^{2}}} \exp \left\{-\frac{1}{2 \sigma_{e^{2}}}\left(Y_{i j}-\theta_{i}\right)^{2}\right\}\right] \frac{b_{2}^{a_{2}}}{\Gamma\left(a_{2}\right)}\left(\frac{1}{\sigma_{e^{2}}}\right)^{a_{2}+1} \exp \left(-\frac{b_{2}}{\sigma_{e}^{2}}\right) \\ \propto \left(\frac{1}{\sigma_{e^{2}}}\right)^{a_{2}+\frac{k J}{2}+1} \exp \left\{-\frac{1}{\sigma_{e}^{2}}\left(\frac{1}{2} \sum_{i=1}^{K} \sum_{j=1}^{J}\left(Y_{i j}-\theta_{i}\right)^{2}+b_{2}\right)\right\}$

よって、パラメータ $a_2 + \frac{KJ}{2}, b_2 + \frac{\sum_{i=1}^{K} \sum_{j=1}^{J} (Y_{ij} - \theta_i)^2}{2}$ の逆ガンマ分布になります。

$\theta$ の完全条件付き分布

最後に、 $\theta_j(j=1, \cdots, J)$ をまとめたベクトル $\theta$ の多変量分布を導出します。
こちらはベクトル演算が入るので少しややこしくなります。

$\displaystyle p\left(\theta \mid Y, \mu, \sigma_{\theta}^{2}, \sigma_{e}^{2}\right) \\ \propto p\left(\theta, Y \mid \mu, \sigma_{\theta}^{2}, \sigma_{e}^{2}\right) \\ = p\left(Y \mid \theta, \mu, \sigma_{\theta}^{2}, \sigma_{e}^{2}\right) p\left(\theta \mid \mu, \sigma_{\theta}^{2}, \sigma_{e}^{2}\right) \\ \propto \left[\prod_{i=1}^{K} \prod_{i=1}^{J} \frac{1}{\sqrt{2 \pi \sigma_{e}^{2}}} \exp \left\{-\frac{1}{2 \sigma_{e}^{2}}\left(Y_{i j}-\theta_{i}\right)^{2}\right\}\right] \left[\prod_{i=1}^{K} \frac{1}{\sqrt{2 \pi \sigma_{\theta}^{2}}} \exp \left\{-\frac{1}{2 \sigma_{\theta}^{2}}\left(\theta_{i}-\mu\right)^{2}\right\}\right] \\ \propto \exp \left\{\frac{1}{\sigma_{e}^{2}} \sum_{i=1}^{K} \sum_{j=1}^{J}\left(Y_{i j}^{2}-2 Y_{i j} \theta_{i}+\theta_{i}^{2}\right)+\frac{1}{\sigma_{\theta}^{2}} \sum_{i=1}^{K}\left(\theta_{i}^{2}-2 \mu \theta_{i}+\mu^2 \right)\right\} \\ \propto \exp \left\{\left(\frac{J}{\sigma_{e}^{2}}+\frac{1}{\sigma_{\theta}^{2}}\right) \sum_{i=1}^{K} \theta_{i}^{2}-2\left(\frac{J}{\sigma_{e}^{2}} \sum_{i=1}^{K} \bar{Y}_{i} \theta_{i}+\frac{1}{\sigma_{\theta}^{2}} \sum_{i=1}^{K} \mu \theta_{i}\right)\right\} \\ = \exp \left\{\theta^{T}\left(\frac{J}{\sigma_{e}^{2}}+\frac{1}{\sigma_{\theta}^{2}}\right) \theta-2 \theta^{T}\left(\frac{J}{\sigma_{e}^{2}} \bar{Y}+\frac{1}{\sigma_{\theta}^{2}} \mu \mathbb{1}\right)\right\}$

ただし、 $\bar{Y}_i = \frac{1}{J} \sum_{j=1}^{J} Y_{ij}, \bar{Y} = (\bar{Y}_1, \cdots, \bar{Y}_N)^T$ としました。また $\mathbb{1}$ は1を並べたベクトル、 $\theta^{T}$ はベクトル $\theta$ の転置です。
最後の形から、この分布は多変量正規分布になることが知られています。なお $\theta^{T}$ と $\theta$ に挟まれた行列の逆行列が共分散行列、 $-2\theta^{T}$ の右部分にあるベクトルに左から共分散行列を掛けたものが平均ベクトルになります。整理すると
共分散行列： $\left[ \left(\frac{J}{\sigma_{e}^{2}}+\frac{1}{\sigma_{\theta}^{2}}\right)I \right]^{-1} = \left( \frac{\sigma^2_{\theta} \sigma^2_e}{J \sigma^2_{\theta} + \sigma^2_e} \right) I$
平均： $\left( \frac{\sigma^2_{\theta} \sigma^2_e}{J \sigma^2_{\theta} + \sigma^2_e} \right) I \left(\frac{J}{\sigma_{e}^{2}} \bar{Y}+\frac{1}{\sigma_{\theta}^{2}} \mu \mathbb{1}\right) = \frac{J \sigma^2_{\theta}}{J \sigma^2_{\theta} + \sigma^2_e} \bar{Y} + \frac{\sigma^2_e}{J \sigma^2_{\theta} + \sigma^2_e} \mu \mathbb{1}$

のようになります。

今回のギブス・サンプリングでは、以上の4つの完全条件付き分布から所定の回数サンプリングを繰り返します。まとめると以下の手順になります（サンプリングの順番は論文に合わせました）。

$\mu, \sigma^2_{\theta}, \sigma^2_e, \theta$ の初期値を適当に決める。
$IG \left( a_1 + \frac{K}{2}, b_1 + \frac{\sum_{i=1}^{K} (\theta_i - \mu)^2}{2} \right)$ から $\sigma^2_{\theta}$ をサンプリングする。ただし他のパラメータは一つ前のステップの値を用いる（以降も同様）。
$IG \left( a_2 + \frac{KJ}{2}, b_2 + \frac{\sum_{i=1}^{K} \sum_{j=1}^{J} (Y_{ij} - \theta_i)^2}{2} \right)$ から $\sigma^2_e$ をサンプリング。
$N\left( \frac{\sigma^2_{\theta} \mu_0 + \sigma^2_0 \sum_{i=1}^{K} \theta_i}{\sigma^2_{\theta} + K \sigma^2_0}, \frac{\sigma^2_{\theta} \sigma^2_0}{\sigma^2_{\theta} + K \sigma^2_0} \right)$ から $\mu$ をサンプリング。
$N \left( \frac{J \sigma^2_{\theta}}{J \sigma^2_{\theta} + \sigma^2_e} \bar{Y} + \frac{\sigma^2_e}{J \sigma^2_{\theta} + \sigma^2_e} \mu \mathbb{1} , \left( \frac{\sigma^2_{\theta} \sigma^2_e}{J \sigma^2_{\theta} + \sigma^2_e} \right) I \right)$ から $\theta$ をサンプリング。
以降、2〜5を所定の回数繰り返す。

Rでの実装

では、これをRで実際に計算するプログラムを作っていきましょう。
まずはサンプルデータを作成します。今回は、次のようなモデルからデータが生成されるものとします。

$\displaystyle y_{ij} = \theta_i + e_{ij} \hspace{10pt} (i = 1, \cdots, 6; \hspace{5pt} j = 1, \cdots, 5) \\ \theta_i \sim N(5, 4), \hspace{5pt} e_{ij} \sim N(0, 16)$

準備も含め、データ生成には以下のコードを用いました。

library(tidyverse)
library(MASS)
library(MCMCpack)

set.seed(819)

K = 6
J = 5
mu = 5
s2_theta = 4
s2_e = 16

theta = rnorm(K, mean = mu, sd = sqrt(s2_theta))
e = rnorm(K*J, mean = 0, sd = sqrt(s2_e))
Y = rep(theta, each = J) + e
Ymat = matrix(Y, nrow = K, ncol = J, byrow = T)
Ybar = apply(Ymat, 1, mean)

生成された測定値データ $Y$ は次のようになります。
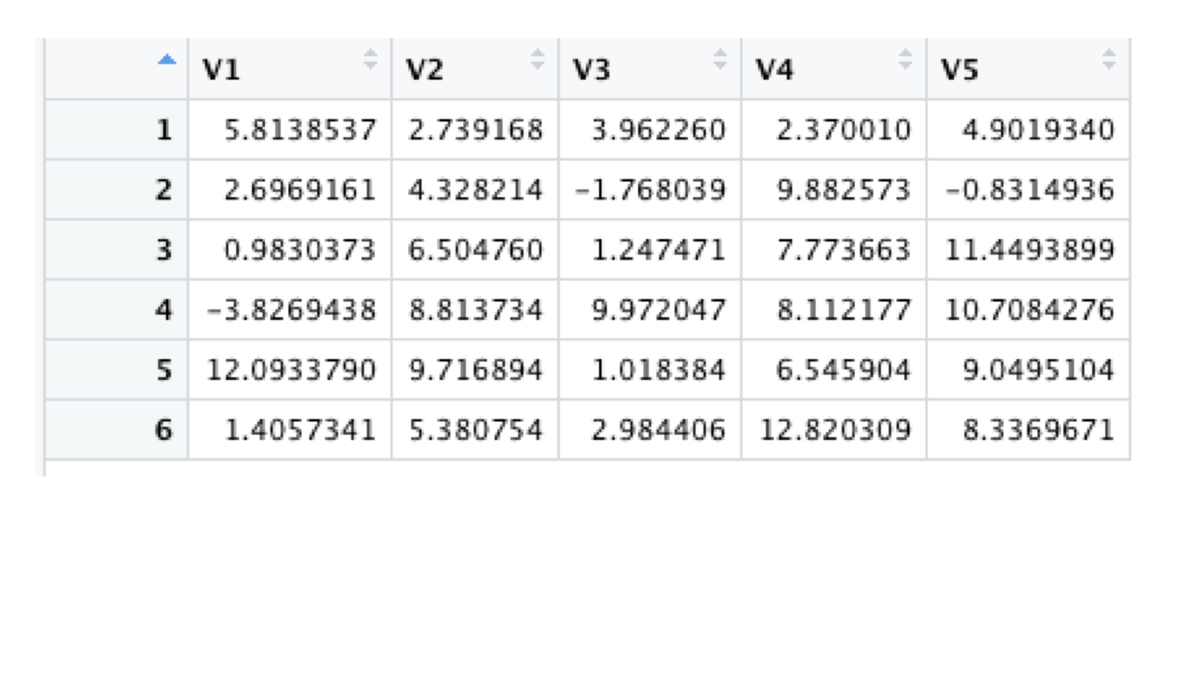
f:id:mstour:20211101190928j:plain

モデルのパラメータにはそれぞれ $\mu = 5, \sigma^2_{\theta} = 4, \sigma^2_e = 16$ という値を設定しています。これらの事後分布が今回の推定対象です。
また各パラメータには「はじめに」で述べたような事前分布を設定しますが、ハイパーパラメータの値は既知としているので、具体的な値を与えます。

$\displaystyle p(\mu) = N(0, 10000), \\ p(\sigma^2_{\theta}) = IG(0.001, 0.001), \\ p(\sigma^2_e) = IG(0.001, 0.001)$

サンプリングの準備として次のような設定を行います。

# MCMC設定
nsamp = 11000
burnin = 1000
thin = seq(burnin+1, nsamp, by = 1)

# hyperparameter
mu_0 = 0
s2_0 = 10000
a_1 = 0.001
b_1 = 0.001
a_2 = 0.001
b_2 = 0.001

# 結果の入れ物
s2_theta_s = array(NA, length(thin))
s2_e_s = array(NA, length(thin))
mu_s = array(NA, length(thin))
theta_s = array(NA, c(K, length(thin)))

# Gibbs sampling初期値
s2_theta_g = runif(1)
s2_e_g = runif(1)
mu_g = runif(1)
theta_g = rep(runif(1), K)

MCMC設定：11000回のサンプリングを行い、そのうち最初の1000回は推定に使用せず捨てることとしています。また、サンプルの間引き(thinning)を行うことを意図したコード（"thin"で定義）にしていますが、今回は間引きは行いませんでした（by=1としています）。
hyperparameter：前述の事前分布のハイパーパラメータです。
結果の入れ物：得られたサンプルを格納するオブジェクトです。ギブス・サンプリングのステップには $\theta$ のサンプリングも含むため、これらのサンプルも格納する必要があります。
Gibbs sampling初期値：前の時点で得られたサンプルの値を計算に使用するので、始まりの値を何らか与えなければなりません。今回は0〜1の間の値のランダムサンプルを用いることにしました。

以下のようなコードで、前半で導出した各パラメータの完全条件付き分布から順繰りにサンプリングを繰り返していきます。逆ガンマ分布のサンプリングに用いた"rinvgamma"関数はパッケージ"MCMCpack"にあります。

### sampling
for(s in 1:nsamp){
  if((round(s/500) - (s/500)) == 0){print(s)}
  # s2_theta
  a = a_1 + K/2
  b = b_1 + sum((theta_g - mu_g)^2)/2
  s2_theta_g = rinvgamma(1, a, b) # MCMCpack
  s2_theta_s[s==thin] = s2_theta_g
  
  # s2_e
  a = a_2 + (K*J)/2
  b = b_2 + sum((Y - rep(theta_g, each = J))^2)/2
  s2_e_g = rinvgamma(1, a, b)
  s2_e_s[s==thin] = s2_e_g
  
  # mu
  a = (s2_theta_g*mu_0 + s2_0*sum(theta_g))/(s2_theta_g + K*s2_0)
  b = (s2_theta_g*s2_0)/(s2_theta_g + K*s2_0)
  mu_g = rnorm(1, mean = a, sd = sqrt(b))
  mu_s[s==thin] = mu_g
  
  # theta
  coef1 = (J*s2_theta_g)/(J*s2_theta_g + s2_e_g)
  coef2 = (s2_e_g)/(J*s2_theta_g + s2_e_g)
  coef3 = (s2_theta_g*s2_e_g)/(J*s2_theta_g + s2_e_g)
  a = coef1 * Ybar + coef2 * rep(mu_g, K)
  b = diag(rep(coef3, K))
  theta_g = mvrnorm(1, mu = a, Sigma = b)
  theta_s[, s==thin] = theta_g
}

推定結果を確認するため、サンプルの要約統計量とトレースプロットを以下のコードで出力しました。
トレースプロットをggplot2で作成するため、サンプルをデータフレームに変換しています。

# 要約統計量
summary(mu_s)
summary(s2_theta_s)
summary(s2_e_s)

# サンプルのトレースプロット
# mu
val = mu_s
mu_df = as.data.frame(val) %>%
  mutate(Iter = 1:length(thin))

ggplot(mu_df, aes(x = Iter, y = val)) + geom_line() +
  geom_hline(yintercept = mu, color = "red") +
  geom_hline(yintercept = median(mu_df$val), color = "blue") +
  labs(y = "mu") + theme_bw()

# s2_theta
val = s2_theta_s
s2_theta_df = as.data.frame(val) %>%
  mutate(Iter = 1:length(thin))

ggplot(s2_theta_df, aes(x = Iter, y = val)) + geom_line() +
  geom_hline(yintercept = s2_theta, color = "red") +
  geom_hline(yintercept = median(s2_theta_df$val), color = "blue") +
  ylim(c(0, 20)) +
  labs(y = "sigma^2_theta") + theme_bw()

# s2_e
val = s2_e_s
s2_e_df = as.data.frame(val) %>%
  mutate(Iter = 1:length(thin))

ggplot(s2_e_df, aes(x = Iter, y = val)) + geom_line() +
  geom_hline(yintercept = s2_e, color = "red") +
  geom_hline(yintercept = median(s2_e_df$val), color = "blue") +
  labs(y = "sigma^2_e") + theme_bw()

計算結果

トレースプロットは以下のようになりました。上から順に、 $\mu, \sigma^2_{\theta}, \sigma^2_e$ です。真の値を赤線、サンプルの中央値を青線で示しました。
ただし $\sigma^2_{\theta}$ は時々非常に大きい値がサンプリングされているため、真の値近辺の結果を確認できるようプロットの範囲を0から20に制限しています。
f:id:mstour:20211031194447p:plain
f:id:mstour:20211031194456p:plain
f:id:mstour:20211031194507p:plain

$\mu, \sigma^2_e$ はおおむね真の値の周辺に分布しているようですが、 $\sigma^2_{\theta}$ は多くのサンプルが0の近辺にある一方、時々大きな値も生成されています。
題材の論文でもこのような結果になっており、さらに事前分布の設定によっても分布の形状が変わるようです。
今回は長くなるのでアルゴリズムの紹介程度にとどめたいのですが、また別の機会にもう少し今回の結果を掘り下げて考えてみたいと思います。
なお、サンプルの要約統計量は以下のようになりました。
f:id:mstour:20211101190941j:plain

おわりに

今回はMCMCのアルゴリズムの一つ、ギブス・サンプリングをRで実施するためのコード作成例を紹介しました。
正しく数式展開をすることに加えて、ソフトウェアのコーディングが間違っていないかも注意深く確かめなくてはならないため、自分で実装するのは正直言ってかなり骨が折れます。
また気力がある時に続編を書ければいいなと思います・・・

参考文献

[1] Gelfand, A. E., Hills, S. E., Racine-Poon, A., & Smith, A. F. (1990). Illustration of Bayesian inference in normal data models using Gibbs sampling. Journal of the American Statistical Association, 85(412), 972-985.

*1:モデルに含まれる他の全部の確率変数で条件付けした確率分布のことです。ギブス・サンプリングを行うには、通常、条件付けした場合の確率分布を数式で書き起こす必要があります。

*2:他の例として、集団 $i$ における個人 $j$ から得られたデータをこのモデルで表現することもできます。

*3:ハイパーパラメータにも事前分布を設定することができますが、今回は具体的な数値を与えることにしています。

*4:厳密には、今回は「他のパラメータで条件つけた」事後分布のことを指します。一方、ややこしいですが、サンプリングによって得られた分布は各パラメータの「完全条件付き」ではない事後分布になります。

*5:このような表現を用いることで、関心あるパラメータに関係のない定数を省略して話を進めることができます。