一元配置分散分析 - 統計学入門一歩先へ

分散分析(Analysis of variance; ANOVA)はさまざまな統計手法の中でもよく知られた方法であるが、最初のうちはなかなかとっつきづらい分野であるように思う。今回は最もシンプルな状況である一元配置（関心のある因子が1つだけの場合のこと）の分散分析の方法を確認し、何をやっているのかを見ていきたい。

何をやっているのか、ざっくり言うとこんな感じ

分散分析も、他のいろいろな統計的検定とロジックは同じで、

帰無仮説(Null hypothesis)が正しいと仮定する
その仮定が正しいとした場合に、今回のデータ以上に極端な値が得られる確率を計算する
その確率が事前に決めた「有意水準(Significance level)」より小さいかどうかを見る

という流れをとる。分散分析では、実験を行う複数の処理（処理の数を $g$ とする）の間に何らかの差があるかどうかを評価することを目的としているため、帰無仮説を「どの処理の間にも（平均に）差がない」つまり

$\displaystyle H_0 : \mu_1 = \mu_2 = \cdots = \mu_g$

と設定する。

そして、「処理の間のばらつき」と「同じ処理を行った個体の間のばらつき」との比を計算して、ある値よりも大きければ、帰無仮説は間違っているだろうと考え、処理の間には何らかの差がある、つまり処理の効果があると判断することになる。このように「ばらつき」の比較を行うため分散分析という名前がついている（のだと思う）。なお、比較するばらつきのことは分散分析の用語で「平均平方(Mean square)」と表現し、「処理の間のばらつき」は処理の平均平方、「同じ処理を行った個体の間のばらつき」は処理以外の原因によるばらつきという意味から誤差の平均平方という。図でもう少し詳しく考えてみよう。

f:id:mstour:20201003070856j:plain

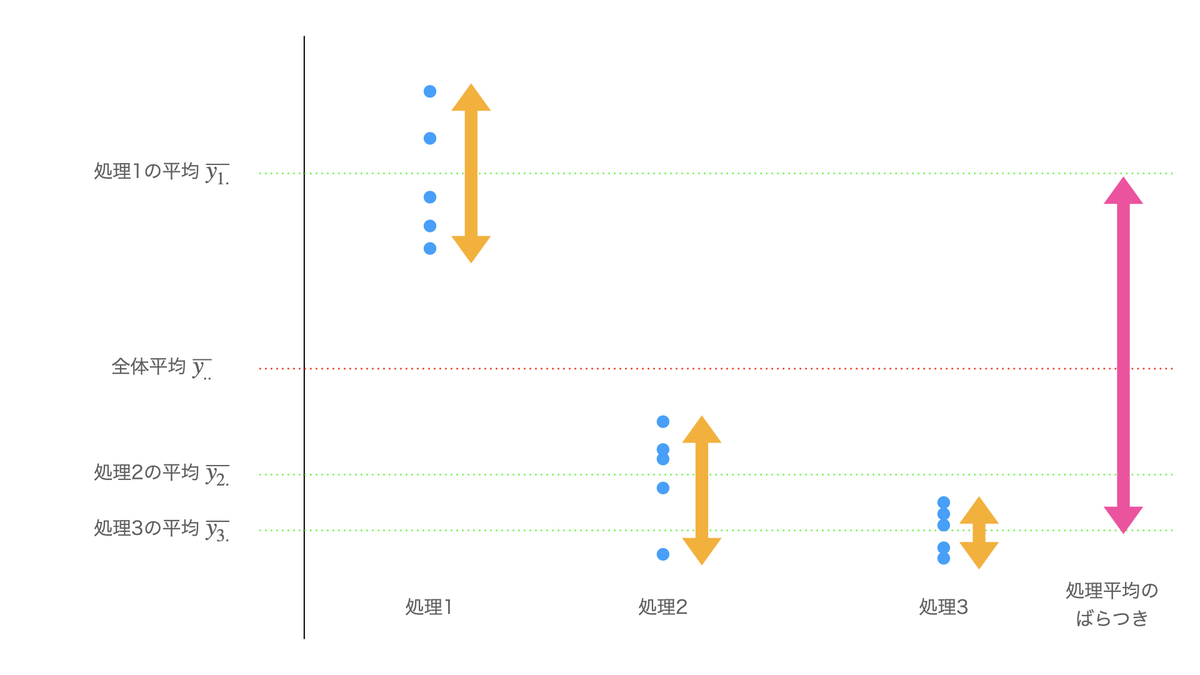
処理1〜3を比較する実験を行い、青丸で示すようなデータが得られたとする（縦軸は結果変数の値）。同じ処理の中でのばらつきは、それぞれの処理の平均を中心としたオレンジ色の矢印で示されている。処理1〜3のばらつきの平均をとったものが誤差の平均平方である。一方で、処理の間のばらつきである処理の平均平方は、全データの平均を中心としたピンク色の矢印（一番右）で示すことができる。
この図を見ると、各処理におけるデータは平均の近くにまとまっている傾向がある一方、処理1の平均は処理2および3の平均に比べかなり大きい。つまり、処理1は偶然では考えられないレベルで処理2・3とは異なった効果を与えることが考えられる。このことは、誤差の平均平方（オレンジの矢印）に比べて処理の平均平方（ピンクの矢印）がかなり大きめになっていることに反映されている。処理の間の違いが大きくなればなるほど、処理の平均平方の大きさは誤差の平均平方よりも大きくなる。
（なお、平均平方は実際にはデータの数や処理の数に依存するので、厳密にはこのように矢印の大きさを比べるだけで判断はできない。説明のための単純化であることをご承知いただきたい。）

きちんとした手順

それでは、一元配置(One-way layout)分散分析について数式を用いて正確な手順を確認していこう。なお、話を単純にするために完全無作為化の場合のみを考え、各処理の反復数も等しいとするが、乱塊法(Randomized block design)を行う場合や、反復数が異なる場合にも同様の方法で解析できる。

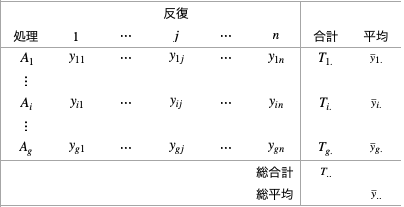
実験データは次のように表現できる。処理を $A$ 、各データの値を $y$ 、合計を $T$ の文字でそれぞれ表している。また処理の数（ここでは、因子の水準数に等しい）を $g$ 、反復数を $n$ とした。

f:id:mstour:20201005221327p:plain

Fisherの3原則に従い、各実験単位には処理が無作為に割り当てられ、それぞれの処理は異なる実験単位に対し複数回実施されているものとする（局所管理については、乱塊法を考えないのでここでは該当せず）。
mstour.hatenablog.com

分散分析では、誤差に起因するばらつきよりも、処理の違いに起因するばらつきの方が十分に大きいかどうかを調べる。そのため、それぞれのばらつきの大きさを定量化する。まずは、処理および誤差に関する平方和(Sum of squares)を計算していく。平方和は平均からのズレの大きさの合計を示す指標で、処理の平方和は「各処理の平均の、全体平均からのズレ」を、誤差の平方和は「各実験単位の、割り当てられた処理の平均からのズレ」を示している。
処理の平方和 $S_A$ 、誤差の平方和 $S_E$ はそれぞれ以下のように計算できる。

$\displaystyle S_A = \sum_{i=1}^{g} \sum_{j=1}^{n}(\overline{y_{i.}} - \overline{y_{..}})^2$

$\displaystyle S_E = \sum_{i=1}^{g} \sum_{j=1}^{n}(y_{ij} - \overline{y_{i.}})^2$

次に、これを用いて比較すべきばらつきの大きさを算出する。ばらつきの大きさとして、平方和を自由度(Degrees of freedom)で割った値である平均平方(Mean square)を用いる。
自由度とは、おおざっぱに言うと、平均値を固定したときに自由に値を変えることのできるデータの数を指している。どういうことかと言うと、いま5個のデータ2, 3, 4, 5, 6とその平均値4を考えてみる。次に、5個のデータの先頭から4つの数字を順番に、2→1, 3→2, 4→3, 5→4に変更してみよう。すると、平均値が4であるためには合計が20でないといけないので、最後の数字は10にしなければならない。つまり自由に値を変更できるのは5個のデータのうち4つしかないので、自由度は4ということになる。もう少し数学的に言うと、自由度とは「計算の対象となるデータの数から、制約条件の数を引いたもの」である。

分散分析の話に戻ると、処理の平方和に関する自由度は、処理の数 $g$ から全体平均の数1を引いた $\nu_A = g-1$ 、誤差の平方和に関する自由度は、データの数 $gn$ から処理の数 $g$ を引いた $\nu_E = g(n-1)$ となる。
平均平方は、平方和を自由度で割ったものであり、処理の平均平方 $V_A$ 、誤差の平均平方 $V_E$ はそれぞれ以下の通りとなる。

$\displaystyle V_A = \frac{S_A}{\nu_A} = \frac{1}{g-1} \sum_{i=1}^{g} \sum_{j=1}^{n}(\overline{y}_{i.} - \overline{y}_{..})^2$

$\displaystyle V_E = \frac{S_E}{\nu_E} = \frac{1}{g(n-1)} \sum_{i=1}^{g} \sum_{j=1}^{n}(y_{ij} - \overline{y}_{i.})^2$

さて、あともうちょっと。ばらつきの大きさを比較するには、誤差の平均平方に対する処理の平均平方の比 $F_A = V_A / V_E$ を用いる。この比はF比(F ratio)といい、分散分析で統計学的な検定をするための統計量である。「どの処理の（真の）平均の間にも差がない」という帰無仮説

$\displaystyle H_0 : \mu_1 = \mu_2 = \cdots = \mu_g$

が正しいものと仮定すると、F比は1番目の自由度が $\nu_A = g-1$ 、2番目の自由度が $\nu_E = g(n-1)$ のF分布と呼ばれる確率分布に従う。帰無仮説が正しい場合にはF比は1となり、帰無仮説が正しくなければF比は1よりも大きな値をとる（差が大きくなるにつれて、F比の値は大きくなっていく）。
この点を補足する。処理の平均平方、誤差の平均平方の期待値をとると、それぞれ次のようになる。

$\displaystyle E[V_A] = E\left[ \frac{S_A}{\nu_A} \right] = \sigma^2 + \frac{n}{g-1} \sum_{i=1}^{g} \alpha_i^2$

$\displaystyle E[V_E] = E\left[ \frac{S_E}{\nu_E} \right] = \sigma^2$

ただし、 $\alpha_i = \mu_i - \mu (i = 1, \cdots, g)$ は処理 $i$ の効果、つまり処理 $i$ の平均 $\mu_i$ と全体平均 $\mu$ との差である。帰無仮説が正しいと仮定すると、すべての処理の平均は全体平均に等しいことになるので、 $\alpha_i = 0 (i = 1, \cdots, g)$ となる。したがって $E[V_A] = E[V_E] = \sigma^2$ 、つまり処理の平均平方と誤差の平均平方の比は平均的に1となることがわかる。一方、帰無仮説が正しくない場合にはどれかの $i$ で $\alpha_i^2 > 0$ なので、F比は1より大きくなる。

他の統計的な検定と同様に、F比があらかじめ決められた有意水準（5%など）に対応する棄却点を超えた場合、帰無仮説は正しくないだろうと判断する。F分布を用いた検定なのでこれはF検定と言ったりもする。

以上が分散分析の流れである。最後に、分散分析で用いる各種の計算結果は分散分析表(ANOVA table)という表にまとめられるのが一般的である。今回紹介した一元配置・完全無作為化の場合は以下のような表になる。なお上記では触れなかったが、全体の自由度（および平方和）はそれぞれ処理と誤差の自由度（および平方和）を合計したものになっている。このように全体の情報を処理によるものと誤差によるものに分解することが分散分析の本質と言えるだろう。

f:id:mstour:20201005222044p:plain