Pearsonの相関係数とSpearmanの相関係数

相関係数には、いくつかの異なる計算方法があり、その解釈のしかたも異なります。今回は代表的なPearsonの相関係数とSpearmanの相関係数を説明します。

Pearsonの相関係数

一般に相関係数とは、2変数の間の単調な関係性の度合い（一方が増えると他方も増えるという「正の相関」、または一方が増えると他方は減るという「負の相関」）を測る指標として用いられますが、Pearsonの相関係数は、さらに2変数の間の線形な（直線的な）関係性を測るものです。単に「相関係数」というと、Pearsonの相関係数の意味で用いられていることが多いと思います。Pearsonの相関係数は-1から1までの範囲の値をとり、1に近いほど正の相関（正確には線形な関係性）が強い、-1に近いほど負の相関が強いことを表します。

注意が必要なのは、繰り返しになりますが「線形な関係性を評価している」という部分で、いくら2変数の間に意味のある関係性が見られる場合でも、それが線形関係でない場合にはPearsonの相関係数で関連の強さをとらえることはできません。例えば下の図の左上Aは2変数の間に明らかに二次関数で表される関係性が見て取れますが、Pearsonの相関係数は $r = -0.05$ となり、両者の相関（線形な関係性）はまったくないという結果になります（ただし、これはPearsonの相関係数だけに起因する問題ではなく、相関係数がそもそも変数間の単調な関係性を表す指標であることが大きな理由です。後述するSpearmanの相関係数でも二次の関係性をとらえることはできません。）。

f:id:mstour:20200528073436p:plain — 2変数の様々な関係性と相関係数の例（Schober et al.(2018)より引用）

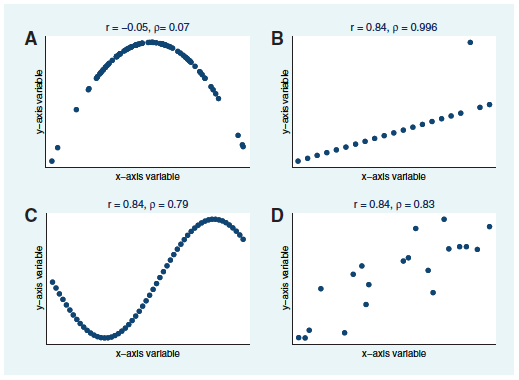
また大きな特徴として、Pearsonの相関係数は、対象とする2変数が正規分布に従っていること（2変量正規分布）を想定しています。 Pearsonの相関係数は以下の式のように2変数間の標本共分散をそれぞれの標本分散の平方根で割ったものとして計算されますが、これは2変量正規分布の相関パラメータを推定していることに相当します。

$r = \frac{ \sum_{i=1}^{n}(x_i - \overline{x})(y_i - \overline{y}) }{ \sqrt{\sum_{i=1}^{n}(x_i - \overline{x})^2}\sqrt{\sum_{i=1}^{n}(y_i - \overline{y})^2} }$

Spearmanの相関係数

さて、Pearsonの相関係数では直線関係ではない場合の関連の強さを適切に評価できませんが、単調な関係性であればSpearmanの相関係数によって測ることができます。Spearmanの相関係数とは、数学的には2変数それぞれの値を「順位」に変換したうえでPearsonの相関係数を計算したものです（データを順位に変換した後は前述の計算式で計算）。Pearsonの相関係数と同様、-1から1の間の値をとり、解釈のしかたも同様です。

これにより、明らかに直線関係ではない変数間の関係について正しくとらえることができます。以下の図のAは2変数の間には単調な関係がありますが、指数関数的な関係性のためPearsonの相関係数は $r = 0.84$ と若干小さい値になっています。一方Spearmanの相関係数は $\rho = 1.0$ であり、完全な単調性があることを示しています。

f:id:mstour:20200531100224p:plain — Pearsonの相関係数とSpearmanの相関係数の違いの例（Schober et al.(2018)より引用）

このようにSpearmanの相関係数は直線でない関係性にも使用できるほか、外れ値に影響されにくい、連続データ以外にも使用できるといった利点があります。しかし、Spearmanの相関係数も単調な関係性を評価するものであるため、最初の図のような二次関数で表される関係性を捉えることはできないことに注意が必要です。

参考文献

Schober P. et al. (2018), "Correlation Coefficients: Appropriate Use and Interpretation", Anesth Analg.