多重比較の前に分散分析をやらないといけないの？

多重比較 実験計画法 検定

はじめに

また今回もちょっとした覚え書き程度の内容ですが・・・時々ご相談を受けたりするテーマなので、少し整理しておきたいと思います。

連続データに関して、ある要因の水準が異なる複数グループ間の比較を行うようなとき*1、第一種の過誤確率*2をコントロールするために多重比較法を用いることがあります。

このような場面では「まず分散分析をやって、統計的有意になった場合のみ続けて個々のグループ間の比較を（多重比較法を用いて）行う、という手順を踏まないといけない」という説があります。
ですが、この主張は必ずしも正しくなく、むしろ適切でない結果を招くことがあります。
実際には分散分析をやらないといけない場合とそうでない場合とがあり、これは用いる多重比較法によって異なってきます。

今回は多重比較法のうち基本的といわれる4つを取り上げ、どれを使用する際に分散分析が必要なのか・不要なのかを整理してみます。
取り上げる多重比較法は以下の通りです。

  • Fisher（フィッシャー）の制約付きLSD法*3
  • Scheffe（シェフェ）の方法*4
  • Dunnett（ダネット）の方法
  • Tukey（テューキー）の方法

なお今回の話題は、1要因の効果を調べる場合（一元配置計画）において問題となることが多いので、その場合に話を限定することにします。


分散分析をやらないといけない場合

今回取り上げる4つの方法のうち、最初に分散分析を行う必要があるのは「Fisherの制約付きLSD法」と「Scheffeの方法」です。
それぞれの方法の概要と、なぜ分散分析をやらないといけないのかを簡単に説明します。

Fisherの制約付きLSD法(Fisher's Protected Least Significant Difference)

この方法は多群の比較において
(1)まず、すべての群の平均が等しいかどうかについて分散分析を行い、
(2)統計的有意だった場合（「すべての群の平均が等しい」という仮説が棄却された場合）のみ、続けて任意の2群の間の比較*5を行う
という手順をとります。

f:id:mstour:20210928194734j:plain

基本的な多重比較法の多くは、第一種の過誤確率が増大することを防ぐために検定の棄却限界値を調整（有意になりにくくなる）します。
一方、Fisherの制約付きLSD法では、「3群の場合に限り」そのような調整を行わずとも第一種の過誤確率が事前に決めた水準に抑えられます。ただし上記手順の(1)にて、分散分析が有意になるという条件を満たしていなければなりません*6。
このような方法なので、最初に分散分析を行わなければなりません。

Scheffeの方法

この方法は、「対比(Contrast)を使って表現することのできる帰無仮説のすべて」を検定したとしても第一種の過誤確率が所定の値を超えないようにする方法です。

対比について少し説明します。
対比とは各群の母平均どうしの足し算・引き算のいろいろなパターンのことで、数学的には次のように表します。

\displaystyle \sum_{i=1}^{a} c_i \mu_i \hspace{10pt} ただし, \sum_{i=1}^{a} c_i = 0

ここで \mu_iは群iの母平均、aは群の数を表しています。
c_iは分析者が値を指定できる定数で、値を変えることでさまざまな対比を作ることができます。
例えば c_1 = 1, c_2 = -1, c_3 = c_4 = \cdots = c_a = 0とすれば \mu_1 - \mu_2という対比ができます。

また、対比を使って表現できる帰無仮説とは、次のように対比を0に等しいとした形のものです：

\displaystyle H_0 : \sum_{i=1}^{a} c_i \mu_i = 0

先の例では、 \mu_1 - \mu_2 = 0、つまり \mu_1 = \mu_2という帰無仮説を表せます。

ここからわかるように、2群間の比較における帰無仮説 \mu_i = \mu_jはすべて対比で表すことができます。
また、 \frac{\mu_1 + \mu_2}{2} = \frac{\mu_3 + \mu_4}{2}のような帰無仮説も対比を使って表せます。
このように、対比を使って表現できる帰無仮説は、単純な2群間の比較だけでなく無数に存在します。
これらのありとあらゆる比較を行っても第一種の過誤確率をコントロールするよう設計されているため、他の多くの多重比較法と比べて検出力が小さい（有意になりにくい）という特徴があります。

f:id:mstour:20210928194802j:plain

Scheffeの方法でも、データから計算される検定統計量が所定の棄却限界値を超えるかどうかを判定します。
この検定統計量は検定する帰無仮説によって値が変わってくる*7のですが、検定統計量の最大値（一番有意になりやすい帰無仮説の検定に使われます）が分散分析で用いるF統計量に等しいことが知られています。
したがって、分散分析で有意でないならば、Scheffeの方法で有意になるような比較（帰無仮説）は存在しないことになります。
最初に分散分析を行って有意であることを確かめておかなければ、Scheffeの方法による以降の手順には意味がなくなると言えるでしょう*8。


分散分析をやらなくてもいい（やってはいけない）場合

事前に分散分析を行わなくてもいい、むしろ行うべきではないのは「Dunnettの方法」と「Tukeyの方法」です。
行うべきでない理由は両者に共通していて、それは「分散分析で有意ではないのに、Dunnettの方法（Tukeyの方法）で有意になる」、また「分散分析で有意なのに、Dunnettの方法（Tukeyの方法）で有意にならない」ということがあり得るからです。つまり、分散分析の結果と2群間比較の結果とが矛盾してしまいます。

以下で述べるように、Dunnettの方法・Tukeyの方法はいずれも分散分析とは無関係に行うことができます。

Dunnettの方法

「ある1つの対照群とその他の各群」との2群間比較を行う場合に用いることのできる方法です。
つまり、対照群を群1、群の数をaとすると、行う比較は「群1と群2」、「群1と群3」、・・・、「群1と群a」の合計a-1個です。
（以前の記事「基本的な多重比較法」でもご紹介しました。）
f:id:mstour:20210928193706j:plain


具体的には、以下の検定統計量を使用します。

\displaystyle t_{1j} = \frac{\overline{x}_1 - \overline{x}_j}{\sqrt{V_E \left( \frac{1}{n_1} + \frac{1}{n_j} \right)}}

ただし j = 2, \cdots, aで、 \overline{x}_1は群1の標本平均、 \overline{x}_jは群jの標本平均、 n_1, n_jはそれぞれ群1と群jのサンプルサイズ、 V_Eはすべての群のデータから計算した標本分散（分散分析では誤差分散と呼ばれます）です*9。
統計量 t_{1j}がDunnettの方法専用の棄却限界値よりも大きければ、群1と群jの間には有意な差があると判定します*10。

Dunnettの方法による多重比較を行った結果として、例えば「群1と群2には差がある」、「群1と群3には差がない」、・・・、「群1と群aには差がある」という計a-1個の結論が得られます。

このように、手順としては2つの群の間の差を評価するだけであり、分散分析のF統計量を用いた群全体の評価は全く行っていません。

Tukeyの方法

Tukeyの方法は、「すべての2群の組み合わせの比較」を行うことを前提とした方法です。つまり、群の数がa個の場合 \frac{a(a-1)}{2}個の比較を行うことになります。
対照群との比較だけを扱うDunnettの方法よりもかなり多くの比較を行いますが、第一種の過誤確率は所定の値に抑えられるように設計されています。ただしその分検出力は小さく（有意になりにくく）なります。
f:id:mstour:20210928193726j:plain

Dunnettの方法と同様に、検定統計量は以下のものを用います。違いは、任意の群iと群jの比較が可能であるという点です。

\displaystyle t_{ij} = \frac{\overline{x}_i - \overline{x}_j}{\sqrt{V_E \left( \frac{1}{n_i} + \frac{1}{n_j} \right)}}

棄却限界値についてもTukeyの方法のためのものが用意されています。
Dunnettの方法と同じ理由で、Tukeyの方法でも事前に分散分析を行うべきではないと言えるでしょう。


おわりに

今回は基本的な多重比較法のうちの4つを取り上げ、それぞれ分散分析を事前に行わないといけないのかどうかを確認しました。
多重比較法はこの他にも非常に多くの種類があるため、この4つの方法だけを根拠に一般論を述べることは難しいですが、基本的な考え方として「用いる多重比較法が分散分析の実施を前提としている場合に限り、最初に分散分析を行う」という方針でよいのではないかと思います。

ただ、複数の比較を行う際にいつも多重比較法を使わなければいけないかというと、必ずしもそうではありません。
多重比較法は確かに第一種の過誤確率をコントロールできる方法ですが、多くの場合検出力を多少犠牲にしてしまうため、本当は意味のある差があるのにその差を見逃してしまうリスクが高まります。
分析の目的に応じて、多重比較法を使うべきかどうか検討するのがよいのではないでしょうか。

参考文献

[1] 永田靖. (1998). 多重比較法の実際. 応用統計学, 27(2), 93-108.
[2] 永田靖, 吉田道弘. (1997). 統計的多重比較法の基礎. サイエンティスト社.

*1:例えば3種類の薬剤の効果を比較する、とか、5種類の肥料の効果を比較する、といった状況を考えてください。

*2:ここでいう第一種の過誤確率とは、1つ1つの検定についてのものではなくて、行おうとしているすべての検定で1回でも間違って有意と判断してしまう確率を意味しています。この確率をFamily Wise Error Rate(FWER)といいます。さらにFWERは真実の状態（例えば、群1と群2の母平均に差はないが、群3、群4とは互いに差がある、など）によって値が変わりますが、真実の状態は当然僕たちにはわかりません。そのため、多重比較法ではFWERのうち考えうる最大のものを所定の値（例えば5%）に抑えることを目標とします。

*3:ただしこの方法で多重性の問題に対応できるのは、3群比較の場合に限ります。4群以上になると第一種の過誤確率をコントロールできないことが知られています。

*4:本当は最後の「e」の上にアクセントの点がつきますが、表示できないのでこの記載で通します。

*5:「対比較」と言うことがあります。

*6:これが、多重比較の前に分散分析を行うという手順のルーツではないかという説があります。

*7:対比の設定に使用する定数 c_iが検定統計量に含まれています。

*8:しかしながら、Fisherの制約付きLSD法のように多重比較法としての妥当性が崩れるわけではないので、分散分析を「行わなければならない」かと言うと微妙な気がします。

*9:通常の2標本t検定との違いは分散 V_Eだけです。

*10:具体的にどのような棄却限界値を用いるかについては、かなり込み入った話になるので今回は立ち入っていません。もちろん知っておくに越したことはありませんが、実用上そこまで困ることはないかと思います。

欠測データ分析シミュレーションのための実戦練習：(1)1変数の欠測

R 欠測データの解析

はじめに

過去2回、Rのmiceパッケージを用いた欠測データの作成方法を紹介してきました。
（過去の記事は以下です。）
mstour.hatenablog.com
mstour.hatenablog.com

今回はもう少し踏み込んで、欠測データ分析に関する実際のシミュレーション研究の再現をしてみたいと思います。題材はSullivanらによる下記の論文です。
（こちらはどの環境からでもアクセスできると思うのですが、見れなかったらすみません。）
www.ncbi.nlm.nih.gov

この論文は欠測メカニズムがMARである様々な欠測データを作成し、ランダム化比較試験における多重代入法・混合効果モデル・欠測を無視した解析の性能比較などを行なったものです。

なお、今回は色々事情があってmiceパッケージのampute関数は使わないことにしました。
理由は、各変数の欠測への影響度を設定することが思いのほか難しいためです。

どういうことかと言うと、複数の変数間の相対的な重みの設定は引数weightsにより行えるのですが、ある変数の絶対的な影響度、つまり回帰係数を具体的にいくつにするという設定を直接行う方法がないようなのです。具体的には変数 y_iの欠測確率を以下のロジスティック回帰モデル

\displaystyle \log \left( \frac{\pi_i}{1-\pi_i} \right) = \beta_0 + \beta_1 x_i + \beta_2 z_i

で与えるものとすると、変数 x_iと z_iのどちらがより欠測への影響が大きいかは引数weightsで指定することができる一方、係数 \beta_1と \beta_2の値を直接指定することができないということです。

もちろん上手く設定する方法はあるのかもしれませんが・・・色々な資料やソースコードを見る限りでは現時点で解決することができませんでしたので、今回は自分でプログラムを作って欠測データを発生させることにします。


シミュレーション研究の設定

さて、今回題材とする研究は、ランダム化比較試験でデータの欠測が発生した場合に、多重代入法はお勧めできる対処法なのか？を検討したものです。
本記事では、最初の例として挙げられている以下のシミュレーションを行い、論文内のFigure 1を再現してみます。

2つの治療をランダムに割り当てる状況を想定し、アウトカムにはある一つの共変量が影響しているものとします。
まずは欠測のない完全データを用意します。
具体的にはアウトカムを Y_i、治療を表す変数を T_i（試験治療の場合に1、対照治療の場合に0となるものとします）、共変量を X_i、誤差を e_iとし、次のモデルからデータを生成します。

\displaystyle Y_i = 0.30 T_i + 0.70 X_i + e_i \hspace{20pt} (i = 1, \cdots. N)

ただし X_i, e_iはそれぞれ互いに独立に標準正規分布に従うものとします。
Rを用いたデータの生成方法は後述します。

次に、完全データのアウトカム Y_iの一部を人為的に欠測させます。
欠測のパターンとして以下の3つを考え、それぞれに対応する欠測データを作ります。

欠測パターン1（MAR X）：欠測メカニズムはMARで、欠測はXにのみ依存する。Xが1標準偏差大きくなるごとに、欠測するオッズ*1は2.5大きくなる。

欠測パターン2（MAR X+T）：欠測メカニズムはMARで、欠測はXおよびTに依存する。Xが1標準偏差大きくなるごとに、欠測するオッズは2.5大きくなる。また対照治療の欠測するオッズは試験治療より2.5大きい。

欠測パターン3（MAR X×T）：欠測メカニズムはMARで、欠測はXおよびTに依存する。Xが1標準偏差大きくなるごとに、欠測するオッズは2.5大きくなる。また X >0のとき対照治療の欠測オッズが試験治療より2.5大きくなり、 X \leq 0のとき試験治療の欠測オッズが対照治療より2.5大きくなる。

ちょっとややこしくなりましたが、ロジスティック回帰モデルで上記1〜3の欠測確率を表現すると、それぞれ次のようになります。

欠測パターン1：

\displaystyle \log \left( \frac{\pi_i}{1-\pi_i} \right) = \beta_0 + 2.5 X_i \\

欠測パターン2：

\displaystyle \log \left( \frac{\pi_i}{1-\pi_i} \right) = \beta_0 + 2.5 X_i - 2.5 T_i \\

欠測パターン3*2：

\displaystyle \log \left( \frac{\pi_i}{1-\pi_i} \right) = \beta_0 + 2.5 X_i - 2.5 T_i I(X_i > 0) + 2.5 T_i I(X_i \leq 0)

\beta_0は、 Y_iが欠測する割合を何%にするかに応じて適切な値を決める必要があります。

今回は欠測の割合を50%に設定するのですが、対応する \beta_0の値を数学的にまともに算出するのはかなり大変なようですので*3、今回はロジスティック回帰モデルの式を \beta_0について整理した上で、 X_i, T_iにそれぞれの期待値を、 \pi_iに0.5を代入するというざっくりした方法で \beta_0を求めます。
具体的には以下の数値になりました。後ほど、欠測割合が意図する通りになっていることを確認します。

欠測パターン1： \beta_0 = 0
欠測パターン2： \beta_0 = 1.25
欠測パターン3： \beta_0 = 0

最後に、作成した欠測データに対して分析を行います。分析方法は以下の3つを試します。

  1. TとXを説明変数とする線形モデル（欠測に関与するXを考慮した分析）
  2. TとXを用いてYを多重代入法で補完し、補完されたデータにTだけを説明変数とする線形モデル*4を使用（欠測に関与するXを考慮した分析）
  3. Tだけを説明変数とする線形モデル（欠測に関与するXを無視した分析）

以上の「完全データ生成」「欠測の発生」「分析」の流れを所定の回数反復することによって、それぞれの方法で平均的に正しい推定が行えるかを評価します。

かなり前置きが長くなりました。では以下で実際にRを使ってシミュレーションをしていきましょう。


シミュレーションコード

シミュレーションを行う前に、まずは毎回行う処理のコードを説明します。
最初に、前述の設定に沿って完全データを作成します。

library(tidyverse)
set.seed(1815)

n = 600
beta1 = 0.3
beta2 = 0.7
T = c(rep(1, n/2), rep(0, n/2))
X = rnorm(n, mean = 0, sd = 1)
e = rnorm(n, mean = 0, sd = 1)
Y = beta1 * T + beta2 * X + e
cd = data.frame(ID = 1:n, T = T, X = X, Y = Y)

試験治療（T=1）と対照治療（T=0）をランダムに割り付けているため、共変量Xの分布が両グループで等しくなるようにデータを生成する必要があります。上記のように完全にランダムに抽出すれば問題ないでしょう。

次に欠測値を発生させます。欠測パターン1〜3に対応する欠測データはそれぞれ以下のように作成できます。

### MAR X
b_1 = 0
missp_1 = 1 / (1 + exp( - (b_1 + 2.5 * X)))
unif_1 = runif(n, min = 0, max = 1)
md_1 = cd %>%
  mutate(missp = missp_1, unif = unif_1) %>%
  mutate(missfl = case_when(missp > unif ~ 1, TRUE ~ 0),
         Y_miss = case_when(missfl == 0 ~ Y))

### MAR X+T
b_2 = 1.25
missp_2 = 1 / (1 + exp( - (b_2 + 2.5 * X - 2.5 * T)))
unif_2 = runif(n, min = 0, max = 1)
md_2 = cd %>%
  mutate(missp = missp_2, unif = unif_2) %>%
  mutate(missfl = case_when(missp > unif ~ 1, TRUE ~ 0),
         Y_miss = case_when(missfl == 0 ~ Y))

### MAR X*T
b_3 = 0
XI = ifelse(X>0, 1, 0)
missp_3 = 1 / (1 + exp( - (b_3 + 2.5 * X - 2.5 * T * XI + 2.5 * T * (1-XI))))
unif_3 = runif(n, min = 0, max = 1)
md_3 = cd %>%
  mutate(missp = missp_3, unif = unif_3) %>%
  mutate(missfl = case_when(missp > unif ~ 1, TRUE ~ 0),
         Y_miss = case_when(missfl == 0 ~ Y))

最初の「MAR X」では、まずmissp_1でロジスティック回帰モデルから各個人の欠測確率を計算し、次に0〜1の値をとる一様乱数を人数分発生させ、乱数の値が欠測確率より小さい場合*5にその個人のデータを欠測させています。他のパターンでも同様です。

欠測割合を50%としていましたが、意図した通りに欠測データが作成できているかを確認しておきましょう。

> sum(is.na(md_1$Y_miss)) / n
[1] 0.4933333

> sum(is.na(md_2$Y_miss)) / n
[1] 0.49

> sum(is.na(md_3$Y_miss)) / n
[1] 0.51

どれも問題ないですね。

欠測データに対する分析は、例えば次のようなコードで実施してみましょう。
ここでは欠測パターン2（XとTが欠測に関与）を例としていますが、他のパターンでも全く同じ方法でOKです。

#----- analysis example(MAR X+T) -----
library(mice)

# adjusted cca
mod_2_1 = lm(Y_miss ~ T + X, data = md_2)
summary(mod_2_1)

# mi overall
pm_2_2 = matrix(c(rep(0, 8), rep(0, 8), rep(0, 8), rep(0, 8),
                  rep(0, 8), rep(0, 8), rep(0, 8),
                  0, 1, 1, 0, 0, 0, 0, 0), nrow = 8, byrow = T)
imp_2_2 = mice(data = md_2, m = 50, method = "norm", predictorMatrix = pm_2_2)
mod_2_2_0 = with(imp_2_2, lm(Y_miss ~ T))
mod_2_2 = pool(mod_2_2_0)
summary(mod_2_2)

# unadjusted cca
mod_2_3 = lm(Y_miss ~ T, data = md_2)
summary(mod_2_3)

多重代入法（上記コードの"mi overall"）は、あらかじめmiceパッケージを読み込んでMICE法で行っています。
欠測の補完モデルの説明変数としてXとTを使う設定にしています。
今回の本題から外れるので詳しい説明は省略し、また別の記事でこの辺りの話を書きたいと思います。
"mod_2_1"、"mod_2_2"、"mod_2_3"に3つの方法それぞれの分析結果を格納しています。

今回実施したシミュレーション用コードの全体は以下の通りです。
所定の繰り返しで得られた治療効果推定値（変数Tの回帰係数です）の平均と標準偏差*6を計算し、題材の論文と同じようなプロットを作成しました。

#----- simulation -----
### parameter setting
nsim = 2000

n = 600
beta1 = 0.3
beta2 = 0.7

b_1 = 0
b_2 = 1.25
b_3 = 0

### MAR X
result_1_1 = NULL
result_1_2 = NULL
result_1_3 = NULL
for (i in 1:nsim){
  # data
  T = c(rep(1, n/2), rep(0, n/2))
  X = rnorm(n, mean = 0, sd = 1)
  e = rnorm(n, mean = 0, sd = 1)
  Y = beta1 * T + beta2 * X + e
  cd = data.frame(ID = 1:n, T = T, X = X, Y = Y)
  missp_1 = 1 / (1 + exp( - (b_1 + 2.5 * X)))
  unif_1 = runif(n, min = 0, max = 1)
  md_1 = cd %>%
    mutate(missp = missp_1, unif = unif_1) %>%
    mutate(missfl = case_when(missp > unif ~ 1, TRUE ~ 0),
           Y_miss = case_when(missfl == 0 ~ Y))
  ### analysis
  # adjusted cca
  mod_1_1 = lm(Y_miss ~ T + X, data = md_1)
  result_1_1 = rbind(result_1_1, mod_1_1$coefficients["T"])
  # mi overall
  pm_1_2 = matrix(c(rep(0, 8), rep(0, 8), rep(0, 8), rep(0, 8),
                    rep(0, 8), rep(0, 8), rep(0, 8),
                    0, 1, 1, 0, 0, 0, 0, 0), nrow = 8, byrow = T)
  imp_1_2 = mice(data = md_1, m = 50, method = "norm", predictorMatrix = pm_1_2)
  mod_1_2_0 = with(imp_1_2, lm(Y_miss ~ T))
  mod_1_2 = pool(mod_1_2_0)
  result_1_2 = rbind(result_1_2, summary(mod_1_2)[2, "estimate"])
  # unadjusted cca
  mod_1_3 = lm(Y_miss ~ T, data = md_1)
  result_1_3 = rbind(result_1_3, mod_1_3$coefficients["T"])
}
mean_1 = c(mean(result_1_1), mean(result_1_2), mean(result_1_3))
sd_1 = c(sd(result_1_1), sd(result_1_2), sd(result_1_3))
summary_1 = data.frame(analysis = c("CCA", "MI overall m=50", "Unadjusted CCA"),
                       mean = mean_1, sd = sd_1)
ggplot(data = summary_1, aes(x = analysis, y = mean, color = analysis)) +
  geom_errorbar(aes(ymin = mean-sd, ymax = mean+sd), width = 0.1) +
  geom_point(size = 3) +
  geom_hline(yintercept = 0.3, linetype = 2, size = 0.3) +
  scale_y_continuous(breaks = c(0.0, 0.3, 0.6, 0.9), limits = c(-0.01, 0.91)) +
  labs(title = "MAR X", x = "", y = "Treatment effect estimate") +
  theme_classic()

### MAR X+T
result_2_1 = NULL
result_2_2 = NULL
result_2_3 = NULL
for (i in 1:nsim){
  # data
  T = c(rep(1, n/2), rep(0, n/2))
  X = rnorm(n, mean = 0, sd = 1)
  e = rnorm(n, mean = 0, sd = 1)
  Y = beta1 * T + beta2 * X + e
  cd = data.frame(ID = 1:n, T = T, X = X, Y = Y)
  missp_2 = 1 / (1 + exp( - (b_2 + 2.5 * X - 2.5 * T)))
  unif_2 = runif(n, min = 0, max = 1)
  md_2 = cd %>%
    mutate(missp = missp_2, unif = unif_2) %>%
    mutate(missfl = case_when(missp > unif ~ 1, TRUE ~ 0),
           Y_miss = case_when(missfl == 0 ~ Y))
  ### analysis
  # adjusted cca
  mod_2_1 = lm(Y_miss ~ T + X, data = md_2)
  result_2_1 = rbind(result_2_1, mod_2_1$coefficients["T"])
  # mi overall
  pm_2_2 = matrix(c(rep(0, 8), rep(0, 8), rep(0, 8), rep(0, 8),
                    rep(0, 8), rep(0, 8), rep(0, 8),
                    0, 1, 1, 0, 0, 0, 0, 0), nrow = 8, byrow = T)
  imp_2_2 = mice(data = md_2, m = 50, method = "norm", predictorMatrix = pm_2_2)
  mod_2_2_0 = with(imp_2_2, lm(Y_miss ~ T))
  mod_2_2 = pool(mod_2_2_0)
  result_2_2 = rbind(result_2_2, summary(mod_2_2)[2, "estimate"])
  # unadjusted cca
  mod_2_3 = lm(Y_miss ~ T, data = md_2)
  result_2_3 = rbind(result_2_3, mod_2_3$coefficients["T"])
}
mean_2 = c(mean(result_2_1), mean(result_2_2), mean(result_2_3))
sd_2 = c(sd(result_2_1), sd(result_2_2), sd(result_2_3))
summary_2 = data.frame(analysis = c("CCA", "MI overall m=50", "Unadjusted CCA"),
                       mean = mean_2, sd = sd_2)
ggplot(data = summary_2, aes(x = analysis, y = mean, color = analysis)) +
  geom_errorbar(aes(ymin = mean-sd, ymax = mean+sd), width = 0.1) +
  geom_point(size = 3) +
  geom_hline(yintercept = 0.3, linetype = 2, size = 0.3) +
  scale_y_continuous(breaks = c(0.0, 0.3, 0.6, 0.9), limits = c(-0.01, 0.91)) +
  labs(title = "MAR X+T", x = "", y = "Treatment effect estimate") +
  theme_classic()

### MAR X*T
result_3_1 = NULL
result_3_2 = NULL
result_3_3 = NULL
for (i in 1:nsim){
  # data
  T = c(rep(1, n/2), rep(0, n/2))
  X = rnorm(n, mean = 0, sd = 1)
  e = rnorm(n, mean = 0, sd = 1)
  Y = beta1 * T + beta2 * X + e
  cd = data.frame(ID = 1:n, T = T, X = X, Y = Y)
  XI = ifelse(X>0, 1, 0)
  missp_3 = 1 / (1 + exp( - (b_3 + 2.5 * X - 2.5 * T * XI + 2.5 * T * (1-XI))))
  unif_3 = runif(n, min = 0, max = 1)
  md_3 = cd %>%
    mutate(missp = missp_3, unif = unif_3) %>%
    mutate(missfl = case_when(missp > unif ~ 1, TRUE ~ 0),
           Y_miss = case_when(missfl == 0 ~ Y))
  ### analysis
  # adjusted cca
  mod_3_1 = lm(Y_miss ~ T + X, data = md_3)
  result_3_1 = rbind(result_3_1, mod_3_1$coefficients["T"])
  # mi overall
  pm_3_2 = matrix(c(rep(0, 8), rep(0, 8), rep(0, 8), rep(0, 8),
                    rep(0, 8), rep(0, 8), rep(0, 8),
                    0, 1, 1, 0, 0, 0, 0, 0), nrow = 8, byrow = T)
  imp_3_2 = mice(data = md_3, m = 50, method = "norm", predictorMatrix = pm_3_2)
  mod_3_2_0 = with(imp_3_2, lm(Y_miss ~ T))
  mod_3_2 = pool(mod_3_2_0)
  result_3_2 = rbind(result_3_2, summary(mod_3_2)[2, "estimate"])
  # unadjusted cca
  mod_3_3 = lm(Y_miss ~ T, data = md_3)
  result_3_3 = rbind(result_3_3, mod_3_3$coefficients["T"])
}
mean_3 = c(mean(result_3_1), mean(result_3_2), mean(result_3_3))
sd_3 = c(sd(result_3_1), sd(result_3_2), sd(result_3_3))
summary_3 = data.frame(analysis = c("CCA", "MI overall m=50", "Unadjusted CCA"),
                       mean = mean_3, sd = sd_3)
ggplot(data = summary_3, aes(x = analysis, y = mean, color = analysis)) +
  geom_errorbar(aes(ymin = mean-sd, ymax = mean+sd), width = 0.1) +
  geom_point(size = 3) +
  geom_hline(yintercept = 0.3, linetype = 2, size = 0.3) +
  scale_y_continuous(breaks = c(0.0, 0.3, 0.6, 0.9), limits = c(-0.01, 0.91)) +
  labs(title = "MAR X×T", x = "", y = "Treatment effect estimate") +
  theme_classic()

分析結果

それぞれの欠測パターンについて、以下のような結果になりました。
f:id:mstour:20210917220928p:plain
f:id:mstour:20210917220937p:plain
f:id:mstour:20210917220945p:plain
論文のFigure 1と同じような図になっていますよね？
論文の結果と同じく、欠測に関与する変数を考慮しない"Unadjusted CCA"では推定にバイアスが入ることがわかります*7。
ただしMAR X+Tの場合のみ、論文よりも推定値がかなり大きくなってしまいました（論文では丸印で示す平均が0.45くらいだが、今回の結果は0.6くらい）。
シミュレーション中に偶然大きな値ばかりが出たのかもしれませんし、論文で書かれていない何らかの情報があるのかもしれませんが、ちょっと原因がわかりませんでした。何かわかったら追記したいと思います。

この結果で重要なのは、どの欠測パターンでも、"CCA"（欠測に関与する変数XとT両方を説明変数とする）と"MI overall"（XとTを説明変数とする補完モデルを用いて多重代入法で欠測を補完する）のどちらもバイアスなく変数Tの効果（治療効果）が推定できているという点です。
欠測メカニズムがMARであれば、欠測に関与する変数で条件付けした分析*8を行えばバイアスなく推定できるため、今回の設定においてはわざわざ多重代入法によって欠測値の補完をしなくてもよい、ということになります。
むしろ多重代入法は通常の線形モデルよりも推定のばらつきが大きくなりがちなので、この場合にはむしろ好ましくないと言えるでしょう*9。
今回作成した図でも、"MI overall"の標準偏差の範囲が"CCA"よりも少しだけ広くなっているのがわかるかと思います。


おわりに

今回は欠測データ分析に関するシミュレーションの実践練習として、統計の研究論文の結果を再現することを試みました。
実務や研究では、経時的データの欠測や多変量の欠測など、もっと複雑な状況のシミュレーションを行わないといけないこともあるかと思います。
次回はもう少し難しい問題を取り上げてみます。

参考文献

[1] Sullivan, T. R., White, I. R., Salter, A. B., Ryan, P., & Lee, K. J. (2018). Should multiple imputation be the method of choice for handling missing data in randomized trials?. Statistical methods in medical research, 27(9), 2610-2626.
[2] Van Buuren, S., & Groothuis-Oudshoorn, K. (2011). mice: Multivariate imputation by chained equations in R. Journal of statistical software, 45(1), 1-67.
[3] Schouten, R. M., Lugtig, P., & Vink, G. (2018). Generating missing values for simulation purposes: a multivariate amputation procedure. Journal of Statistical Computation and Simulation, 88(15), 2909-2930.

*1:少し分かりづらいですが、ロジスティック回帰モデルで欠測確率を計算するためこのような表現になっています。厳密には異なりますが、ここでは「欠測するオッズは2.5大きくなる」は「欠測確率が2.5倍になる」とだいたい同じようなものだと考えてもらっても構いません。

*2: I( )は、かっこの中身の条件に該当する場合に1を、そうでない場合に0となる関数です。例えば I(X_i > 0)は X_iが正の値のときに1、そうでないとき0をとります。

*3:以前の記事で参考にしたampute関数に関するSchoutenらの論文に数学的な導出の説明があります。

*4:要するに、独立な2群のt検定です。

*5:例えば一様乱数が0から0.2の間の値をとる確率は20%なので、欠測確率が20%の個人については一様乱数の値が0.2より小さい時にデータを欠測させればよいことになります。

*6:原論文には「emprical standard error」と記載されていますが、文脈から2000回のシミュレーションで得られた点推定値の標準偏差を示していると思われます。

*7:真の治療効果の値は0.3と設定していました。

*8:繰り返しになりますが、分析モデルの説明変数にこれらの変数を含めればよいということです。

*9:ただし、多重代入法を使った方がよい場合もあります。その話題はまた改めて考えることにします。

ゼロ値を多く含むデータの統計モデル：連続データの場合

統計モデル一般 最尤法 ベイズ統計

はじめに

以前、ゼロの多い離散データの統計モデルの話を書きましたが、今回はその続きとして、連続型データの場合のモデルを紹介していきたいと思います。
mstour.hatenablog.com

離散データの場合には飲酒回数を例として考えました。ゼロの多い連続データの典型例としても、ある期間における飲酒の量が挙げられます。
ただし、こちらは飲んだ「頻度」ではなく「量（mlなどの単位で表される）」が該当します。
全くお酒を飲まない（飲めない）人の飲酒量は常にゼロのため、ヒストグラムを描くとゼロに高い山ができます。
一方、飲酒の習慣がある人についても、飲む量には個人間のばらつきが大きいと考えられ、非常に右に裾の長い分布形になることが考えられます。このような分布形のデータは「Semi-continuous data」と呼ばれます。

その他には、

  • エクササイズにかける時間（運動を全くしない人の時間はゼロ）
  • 喫煙本数（喫煙しない人の本数はゼロ）

などもゼロの多い連続データと言えるでしょう。

このようなデータをうまく表現する方法の1つとして、「ゼロのパート」と「正の値のパート」の2つの要素からなる「Two-part model」があります。
ゼロのパートに関しては「ゼロでない確率 \pi*1をパラメータとする二項分布」、正の値のパートに関しては「正の値のみをとる連続型確率分布」が具体的な構成要素になります。

他には離散型の場合と同様にZero-inflated modelも選択肢になりますが、手元に詳しい資料がないので今回は割愛します。こちらも離散型データの時と考え方は同じですが、連続型分布として「0以上の値をとる」分布を用意する必要があります。0を含む分布は基本的な確率分布の中ではあまり思い当たらないのですが、切断分布(Truncated distribution)を使えば問題ありません。
切断正規分布を用いた例として、例えば以下のようなものがあります。
www.ncbi.nlm.nih.gov

ということで、今回はTwo-part modelに関して話を進めていきたいと思います。


Two-part model

Semi-continuus data Yに対するTwo-part modelは、次のような確率密度関数で表現できます。

\displaystyle f(y) = \left( 1-\pi \right) ^{(1-s)} \times \left[ \pi g(y) \right]^s \hspace{10pt} (y \geq 0)

なお \piは Y \neq 0になる確率、 sは Y = 0のときに0、 Y \neq 0のときに1をとる変数とします。
また g(y)は正の値をとる何らかの連続型確率分布の確率密度関数です。選択肢としては対数正規分布やガンマ分布、さらに複雑な分布も考えることができます。

Two-part modelは、離散型データのモデルとして紹介したHurdle modelと同じ形式になっています。
上の定義の通り、確率 1-\piで値が0になるのですが、この0の値は「常に0になる」場合と「たまたま0になった」場合との両方を含んでいます。
したがって、常に値が0になる人（例えば、お酒を全く飲まない人）と、たまたま値が0だった人（お酒を飲むことはあるが、調査期間中にたまたま全く飲まなかった人）とを区別することができません。
一方、Zero-inflated modelでは「お酒を全く飲まない人」と「たまたま飲酒量が0だった人」の確率分布はモデル内の別々の部分で表されています。ここがTwo-part modelとZero-inflated modelの大きな相違点かと思います。


回帰

離散型データと同様にして回帰モデル(Two-part regression model)を考えることができます。
以下では、モデルの数式を具体的に特定するために、使用する連続型分布として対数正規分布を選択することにします。
対数正規分布は、 \muと \sigmaの2つのパラメータで特徴付けられます。
対数正規分布に従う変数を Yとすると、 \muは対数変換した時の平均 E(\log(Y))、 \sigma^2は同じく対数変換後の分散 V(\log(Y))にあたります。

回帰モデルでは例えば以下のように、平均パラメータ \muと、Two-part modelにおいて値が正になる確率 \piそれぞれをいくつかの説明変数で表現します：

\displaystyle \log \left( \frac{\pi_i}{1-\pi_i} \right) = \beta_{10} + \beta_{11} x_{i11} + \cdots + \beta_{1p} x_{i1p}, \\ \mu_i = E(\log(Y_i)|Y_i > 0) = \beta_{20} + \beta_{21} x_{i21} + \cdots + \beta_{2q} x_{i2q}

離散型データの場合と同様、説明変数は \muに関するモデルと \piに関するモデルとで同じでも異なっていても構いません。

なお平均パラメータ \muは正の値に関する分布（ここでは対数正規分布）に関するパラメータであることに注意する必要があります。
上の式でも出てきているように、このパラメータは「目的変数の値がゼロではない（正の値）という条件のもとでの（言い換えると、 i=1,\cdots,Nのうち Y_i>0だった人に限った）」（対数変換後の）平均を意味しています。
したがってj番目の回帰係数 \beta_{2j}は、「目的変数の値がゼロでない人たちに対する」説明変数 x_{i2j}の効果を示しており、値がゼロだった人は対象に含まれていません。

推測の対象を値がゼロだった人も含む母集団全体へ広げるためには、これも離散型の場合と同様に、母集団平均 E(Y_i)を直接モデリングする「Marginalized model」を考えます。


Marginalized modelでは、値が正になる確率 \piに関する部分は通常のモデルと同じですが、以下のように母集団平均と説明変数とを関連づけます。

\displaystyle \log \left( \frac{\pi_i}{1-\pi_i} \right) = \alpha_{10} + \alpha_{11} x_{i11} + \cdots + \alpha_{1p} x_{i1p}, \\ E(Y_i) = \exp \left( \alpha_{20} + \alpha_{21} x_{i21} + \cdots + \alpha_{2q} x_{i2q} \right)

目的変数の値は0以上であるため、右辺を指数関数で変換しています。
このモデルを用いると、他の説明変数の値が同じである場合、

\displaystyle \frac{E(Y_i|x_{i2j}=x+1)}{E(Y_i|x_{i2j}=x)} = \frac{\exp(\alpha_{2j} x) \exp(\alpha_{2j})}{\exp(\alpha_{2j} x)} = \exp(\alpha_{2j})

より、「j番目の説明変数 x_{i2j}が1単位増加したとき、母集団平均は \exp(\alpha_{2j})倍になる」と解釈することができます*2。

f:id:mstour:20210904144730j:plain

Marginalized modelの回帰係数を推定するためには、回帰係数と対数正規分布のパラメータ \mu_iとを結びつける式を導出して、尤度へ代入する必要があります。
次の式の(1)はMarginalized modelの定義式、(2)はTwo-part modelの確率密度関数を用いて Y_iの期待値を求めています。 g(y)はここでは対数正規分布の確率密度関数です。

\displaystyle (1) E(Y_i) = \exp \left( \alpha_{20} + \alpha_{21} x_{i21} + \cdots + \alpha_{2q} x_{i2q} \right) \\ (2) E(Y_i) = \int_0^{\infty} y_i f(y_i) dy_i = \pi_i \int_0^{\infty} y_i g(y_i) dy_i = \pi_i \exp \left( \mu_i + \frac{\sigma^2}{2} \right)

(1)(2)それぞれの右辺が等しいので、 \mu_iについて整理すると

\displaystyle \mu_i = \alpha_{20} + \alpha_{21} x_{i21} + \cdots + \alpha_{2q} x_{i2q} - \log(\pi_i) - \frac{\sigma^2}{2}

となり、Two-part modelの尤度を回帰モデルのパラメータで表すことができます（ \pi_iの部分にも前に定義したモデルを代入します）。


おわりに

0の多い連続型データに対しても、離散型データの場合の「Hurdle model」や「Zero-inflated model」と同様の統計モデルを用いることができます。
今回はそのうちの一つ「Two-part model」を紹介しました。
正規分布などの標準的な分布を無理に当てはめたり、データの変数変換やカテゴリ化を行うことなく、現象の振る舞いをより自然にモデルで表現できることが大きな魅力かと思います。
なお正の値の確率分布としては対数正規分布のほか「Skew lognormal distribution（対数歪正規分布？）」や「一般化ガンマ分布」などが提案されています。


参考文献

[1] Nguyen, CD, Moreno-Betancur, M, Rodwell, L, Romaniuk, H, Carlin, JB, Lee, KJ. Multiple imputation of semi-continuous exposure variables that are categorized for analysis. Statistics in Medicine. 2021; 1– 14.
[2] Smith, V. A., Preisser, J. S., Neelon, B., and Maciejewski, M. L. (2014), A marginalized two-part model for semicontinuous data, Statist. Med., 33, 4891– 4903.
[3] Neelon, B., O'Malley, A. J., & Smith, V. A. (2016). Modeling zero‐modified count and semicontinuous data in health services research part 1: background and overview. Statistics in Medicine, 35(27), 5070-5093.
[4] Neelon, B., O'Malley, A. J., & Smith, V. A. (2016). Modeling zero‐modified count and semicontinuous data in health services research part 2: case studies. Statistics in medicine, 35(27), 5094-5112.
[5] Zhang, X., Guo, B., & Yi, N. (2020). Zero-Inflated gaussian mixed models for analyzing longitudinal microbiome data. Plos one, 15(11), e0242073.

*1:「ゼロのパート」と言っていますが、解釈のしやすさと参考文献の表記を踏まえて「ゼロでない確率」を以降では考えます。

*2:Marginalizedでない回帰モデルの場合にはこのような解釈はできず、説明変数の効果は他の説明変数の水準に依存するという特徴があります。

miceパッケージampute関数による欠測データの作成:(2)実行例

R 欠測データの解析

はじめに

今回は、以前の記事で概要を紹介したampute関数を用いて実際に欠測データを作成してみたいと思います。
amputeの概要については、よろしければ以前の記事もご覧ください。
mstour.hatenablog.com


使用するデータセット

まずは今回使用するパッケージとデータセットを読み込んでおきます。
ampute関数を使うためにmiceパッケージを、サンプルデータセットを得るためにlme4パッケージも読み込みます（後述）。
また、後ほどデータの加工やプロットに必要となるtidyverseも読み込んでおきます。
データセットは2種類を使ってみます。

library(tidyverse)
library(mice)
library(lme4)
set.seed(1923)

sampdata_1 = mice::boys
sampdata_2 = lme4::sleepstudy
1. boys データセット

1つめの例は、miceパッケージに入っている「boys」というデータセットです。
これはある年における少年の年齢・身長・体重などの特徴を調べた、cross-sectional dataと呼ばれる形式（大雑把に言うと、ある特定時点のスナップショット）のデータセットです。
このデータセットに対して、「年齢が高くなるほど欠測が起きやすい」という状況を想定して欠測を作りたいと思います。
ただし、boysデータセットにはすでに多くの欠測（NA）が含まれているので、このままではampute関数が使えません。また、文字型の変数もそのままでは使えないので、使いずらい変数や欠測レコードをあらかじめ削除しておくことにします。

sampdata_1r = sampdata_1 %>%
  select(-gen, -phb, -tv, -reg) %>%
  filter(complete.cases(.))

2行目で不要な変数を削除し、3行目でさらに欠測のないレコードだけを残す処理をしています。

2. sleepstudy データセット

2つめの例は、lme4パッケージに入っている「sleepstudy」データセットを用います。
これは睡眠時間制限を連日行い、その期間中に何らかの課題を実施した時の反応時間*1を毎日記録したもので、このようなデータセットはlongitudinal dataと呼ばれます。
この例では、「前日の測定値が当日欠測するか否かに影響する」というパターンを考えてみます。

なお、ampute関数では（というか、miceパッケージでは*2）データセットを横持ち（つまり、日々の測定値はそれぞれ別変数として保存され、横に広い形になる）にしておく必要があります。
sleepstudyデータセットは各個人の反復測定データが縦に並んだ（縦持ちの）形状なので、以下のように加工しておきます。

sampdata_2r = sampdata_2 %>%
  pivot_wider(names_from = Days, values_from = Reaction, names_prefix = "Day")

測定値の変数名として、測定日の数値の前に"Day"をつけることにしました。


事例1. boys データセット

早速1つめの例で欠測データを作っていきましょう。

前回ご紹介したように、ampute関数では欠測パターンや欠測割合など、いくつかのパラメータを指定する必要があります。

f:id:mstour:20210826071029j:plain

パラメータの与え方で少し手間取る可能性があるので、まずはいくつかのパラメータ情報の形式を確認してみましょう。
デフォルト設定でamputeを適用した後、設定を確認します。

defo_1 = ampute(sampdata_1r)
ptn_defo_1 = defo_1$patterns
frq_defo_1 = defo_1$freq
wgt_defo_1 = defo_1$weights

欠測パターンは、次のような行列型で定義されます。

> ptn_defo_1
  age hgt wgt bmi hc
1   0   1   1   1  1
2   1   0   1   1  1
3   1   1   0   1  1
4   1   1   1   0  1
5   1   1   1   1  0

各行が今回用いられた欠測パターンを表しており、0が欠測する変数、1が欠測しない変数を示します。
つまり、1行目のパターンは「ageのみが欠測する」、2行目は「hgtのみが欠測する」となり、合計5つの欠測パターンが存在していることになります。
自分で欠測パターンを定義するには、このルールにそって行列を作る必要があります。

各欠測パターンの起こる割合は、次のようなベクトル形式で表します。

> frq_defo_1
[1] 0.2 0.2 0.2 0.2 0.2

デフォルトでは、すべてのパターンの割合が等しくなるように設定されるようです。

各変数が欠測へ与える影響の大きさ（重み）は次のような行列形式になります。

> wgt_defo_1
  age hgt wgt bmi hc
1   0   1   1   1  1
2   1   0   1   1  1
3   1   1   0   1  1
4   1   1   1   0  1
5   1   1   1   1  0

この行列の1〜5行は、それぞれ欠測パターン1〜5に対応しています。
数値の大きさは欠測へ与える影響の大きさを示しており、0は欠測に全く関係しないことを意味しています。
したがって、1行目は欠測パターン1の「ageのみ欠測」にどの変数がどの程度影響するかを定義しており、デフォルトでは「age自身は欠測に影響せず、それ以外の変数は等しい影響度を持つ」という設定になっています*3。

そのほかのパラメータは基本的に数値をそのまま与えるだけなので、以上の点に注意すればよいでしょう。


では、ここからは設定を自分で決めて、欠測データを作ってみることにします。
最初に述べたように、年齢が高くなるほど欠測が多いようなデータを作ります。

まずは欠測パターンを定義します。
話を単純にするために、以下のような欠測パターンだけを考えることにします。

  • 身長（hgt）だけが欠測する
  • 身長（hgt）と体重（wgt）が欠測する

なお、本来はどちらの場合でもBMI（bmi）は計算できませんが、ここではそれは考えないことにします。
上記の2パターンの欠測を定義するには、次のように行列を用意すればOKです。

ptn_1 = matrix(c(1, 0, 1, 1, 1,
                 1, 0, 0, 1, 1),
               nrow = 2, byrow = T)
colnames(ptn_1) = colnames(sampdata_1r)

ptn_1
> ptn_1
     age hgt wgt bmi hc
[1,]   1   0   1   1  1
[2,]   1   0   0   1  1

次に各欠測パターンの割合は、身長のみが70%、身長・体重の両方が30%としておきます。

frq_1 = c(0.7, 0.3)

欠測に対する各変数の影響の重みについては、

  • 年齢のみが欠測に影響する
  • 欠測する変数自身の値は関係しない

という設定とします（欠測メカニズムで言うとMARとなります）。

wgt_1 = matrix(c(1, 0, 0, 0, 0,
                 1, 0, 0, 0, 0),
               nrow = 2, byrow = T)
colnames(wgt_1) = colnames(sampdata_1r)

wgt_1
> wgt_1
     age hgt wgt bmi hc
[1,]   1   0   0   0  0
[2,]   1   0   0   0  0

これらの設定を使ってamputeを実行します。欠測レコードの割合はprop = 0.4としました。

amp_1 = ampute(sampdata_1r, patterns = ptn_1, freq = frq_1, weights = wgt_1, prop = 0.4)
miss_1 = amp_1$amp

意図した通りに欠測データが作成されたかを確認してみましょう。
欠測（NA）の数を見るにはsummaryが手っ取り早いです。

summary(miss_1)

> summary(miss_1)
      age              hgt              wgt              bmi              hc       
 Min.   : 0.035   Min.   : 50.00   Min.   :  3.14   Min.   :11.77   Min.   :33.70  
 1st Qu.: 1.534   1st Qu.: 74.28   1st Qu.: 10.77   1st Qu.:15.86   1st Qu.:48.27  
 Median :10.410   Median :101.40   Median : 30.95   Median :17.37   Median :53.20  
 Mean   : 9.109   Mean   :114.09   Mean   : 35.09   Mean   :17.99   Mean   :51.60  
 3rd Qu.:15.169   3rd Qu.:156.50   3rd Qu.: 56.90   3rd Qu.:19.40   3rd Qu.:56.00  
 Max.   :20.813   Max.   :196.70   Max.   :117.40   Max.   :31.74   Max.   :65.00  
                  NA's   :282      NA's   :92

レコード数684なので、hgtは282 / 684 * 100 = 41.2%、wgtは92 / 684 * 100 = 13.5%が欠測しています。
全体の欠測レコードの割合は40%になるようにしていましたので、hgtは指定に近い欠測割合となっています。
またwgtが欠測する割合は0.4 * 0.3 * 100 = 12%になるよう設定していましたが、こちらもほぼ狙い通りになっているようです。

年齢が高いほど欠測が多いかどうかは、散布図を描いて確認してみます。
元のデータと欠測を発生させたデータのそれぞれについて、横軸を年齢、縦軸を身長とした散布図を作成します。

ggplot(data = miss_1, aes(x = age, y = hgt)) + geom_point() + labs(title = "amputed")
ggplot(data = sampdata_1, aes(x = age, y = hgt)) + geom_point() + labs(title = "original")

f:id:mstour:20210824071114p:plain
f:id:mstour:20210824071124p:plain

上が欠測データ、下が元データです。右の方に行くほどデータ点がスカスカになっているのがわかるでしょうか？


事例2. sleepstudy データセット

sleepstudyデータセットについても、同じ要領で欠測を発生させてみます。
こちらは、毎日繰り返し測定した値が横に並ぶように事前に加工をしていました。
以下のような欠測パターンを考えることにします。

  • 5日目(Day5)から9日目(Day9)までのデータが欠測しうる
  • ある時点のデータが欠測した場合、以降の時点も欠測する*4
  • ある時点のデータが欠測するかどうかは、前の時点の値だけに影響される

このデータは変数が多いため、amputeに与えるパラメータの行列を手入力で作るのは少し面倒です。
そこで、デフォルト設定の行列を加工して使用することにします。
まずは何も指定せずにamputeを実行します。

defo_2 = ampute(sampdata_2r)

> defo_2 = ampute(sampdata_2r)
 警告メッセージ: 
Data is made numeric because the calculation of weights requires numeric data

numeric型以外の変数がデータセットに入っていると警告が出ます。
今回は"Subject"（個人の識別番号）がfactor型だったのが原因*5で、amputeされたデータではnumericに変換されていました。
"Subject"は今回の欠測の発生には関与させない予定なので、ここでは無視して進めます。

欠測パターンと重みの設定をそれぞれ抽出し、編集します。
freqについては、直接入力してもいいでしょう。

# 欠測パターン
ptn_defo_2 = defo_2$patterns
ptn_2 = ptn_defo_2[7:11,]
ptn_2[1, 8:11] = c(0, 0, 0, 0)
ptn_2[2, 9:11] = c(0, 0, 0)
ptn_2[3, 10:11] = c(0, 0)
ptn_2[4, 11] = 0

frq_2 = c(0.2, 0.2, 0.2, 0.2, 0.2)

wgt_defo_2 = defo_2$weights
wgt_2 = wgt_defo_2[7:11,]
wgt_2[1, ] = c(0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0)
wgt_2[2, ] = c(0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0)
wgt_2[3, ] = c(0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0)
wgt_2[4, ] = c(0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0)
wgt_2[5, ] = c(0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0)

以下のような行列ができます。

> ptn_2
   Subject Day0 Day1 Day2 Day3 Day4 Day5 Day6 Day7 Day8 Day9
7        1    1    1    1    1    1    0    0    0    0    0
8        1    1    1    1    1    1    1    0    0    0    0
9        1    1    1    1    1    1    1    1    0    0    0
10       1    1    1    1    1    1    1    1    1    0    0
11       1    1    1    1    1    1    1    1    1    1    0

> wgt_2
   Subject Day0 Day1 Day2 Day3 Day4 Day5 Day6 Day7 Day8 Day9
7        0    0    0    0    0    1    0    0    0    0    0
8        0    0    0    0    0    0    1    0    0    0    0
9        0    0    0    0    0    0    0    1    0    0    0
10       0    0    0    0    0    0    0    0    1    0    0
11       0    0    0    0    0    0    0    0    0    1    0

それでは、これらを使ってamputeを実行しましょう。

amp_2 = ampute(sampdata_2r, patterns = ptn_2, freq = frq_2, weights = wgt_2, prop = 0.4)
miss_2 = amp_2$amp

どのようなデータセットが作られたかを確認するために、今度は個人ごとの折れ線グラフを作ってみます。
ggplotで折れ線グラフを作るには、縦型のデータを用意する必要があるので、再度データを加工していきます。

# 縦型に変更
miss_2_l = miss_2 %>%
  pivot_longer(cols = c(-Subject), names_to = "Day", names_prefix = "Day", values_to = "Val") %>%
  mutate(Subject = factor(Subject))

# 折れ線グラフ
ggplot(data = miss_2_l, aes(x = Day, y = Val, group = Subject, color = Subject)) + 
  geom_line() + geom_point() + labs(title = "amputed")

以下のようなグラフができました。
f:id:mstour:20210825201147p:plain

Day6以降の測定データが無くなっている人がいるのが分かります（Day5から欠測が起こるように設定していましたが、今回は偶然Day5に欠測が発生しませんでした）。


おわりに

今回は、miceパッケージのampute関数を用いた欠測データの作成例を紹介しました。
実験や調査において、データの欠測が避けられないことはどうしてもあるかと思います。
欠測のあるデータを分析する手法を検討するためにシミュレーションを行いたい場合など、この方法が役に立つ場面があるかもしれません。

参考文献

[1] ampute: Generate missing data for simulation purposes.
https://www.rdocumentation.org/packages/mice/versions/3.13.0/topics/ampute
[2] Multivariate amputation using ampute.
https://mran.microsoft.com/snapshot/2017-02-20/web/packages/mice/vignettes/ampute.html

*1:今回の本題にはあまり関わらないので、詳細には触れません。もしご興味があればマニュアルの引用元をご覧いただけると幸いです。

*2:Rに限らず、例えばSASでも多重代入法は横持ちのデータセットに対してしか使えなかったと思います。

*3:デフォルトで欠測変数自身の重みが0になるのは、デフォルトの欠測メカニズムがMARであるためです。MNARに指定した場合には、欠測変数自身の重みは1になります。なお欠測メカニズムはmech = "MAR"のように指定します。

*4:対象者が調査から「脱落」するような状況です。

*5:変数の値と欠測に与える重み(weights)を用いて欠測する確率を計算する必要があるため、numeric以外の変数型だと内部で処理ができないからと思われます。

ゼロ値を多く含むデータの統計モデル：離散データの場合

カテゴリカルデータ 統計モデル一般

はじめに

今回は少し趣向を変えて、現在僕が関心を持っている（そこまでメジャーではないと思われる方面の）統計モデリングの話題を書いていこうと思います。
ほとんど覚え書きのような内容なので、まあ、こんなんもあるのか、という程度にみてもらえればと思います。詳しくは参考文献や、Wikipediaなんかで・・・

ゼロを多く含むデータ

世の中には性質上多くのゼロが含まれてしまうデータが色々とあります。
医学分野では、例えば特定の期間におけるがん検診の受診回数や外来受診回数などが挙げられます。「全く受診しない」人が一定数いることがしばしばあるため、これらはゼロを多く含むカウントデータという形式になる可能性があります。

カウントデータのモデリングにはポアソン分布や負の二項分布がよく用いられますが、関心ある事象の頻度が偶然ゼロになるだけでなく、ある属性の人はほぼ確実にゼロになる（検診や受診の例だと、健康な人や若い人は受診しない可能性が極めて高いというケースが考えられます）ような場合、これら一般的な確率分布が想定するよりもゼロの頻度がとても多くなることが考えられます*1。

上記のようなデータは「zero modified data*2」と称されることがあります。


連続型（と通常みなすことのできる）データにおいても、似たような状況が生じることがあります。
つまり、ゼロの一点の確率密度と、正の値をとる連続型分布とを組み合わせた分布型でよく表現できるようなデータがこれにあたります。
医学での例としては、ある期間における医療費の額が挙げられます。この場合も、「医療費がかかっていない」人が相当数いるという場合が十分考えられます。
連続型データの場合には、「semi continuous data」と呼ばれます。


これらzero modified dataやsemi continuous dataのモデリング方法としては、「two-part model」と呼ばれるモデルが有用であると言われています。
two-part modelとは、「ゼロ値のパート」と「ゼロでない値（正の値）のパート」の2つの要素のモデルを組み合わせたものです。
離散データに関するモデルとしては「hurdle model」と「zero-inflated model」、連続データについては「two-part semi continuous model」が例として挙げられます。
今回は離散データに用いられる2つのモデルについて整理していきます。


hurdle model

hurdle modelは、「値がゼロになるか・正の値（整数）になるか」を決める確率と、正の値の確率分布との2つの要素でデータを説明します。正の値の確率分布としては、一般的な離散型分布を1以上の値をとるように修正した「切断分布」を利用します。

具体的には、正の値に使用したい切断前の確率分布を p(y|\theta)とすると

\displaystyle P(Y = 0) = 1 - \pi, \\ P(Y = y) = \pi \frac{p(y|\theta)}{1 - p(0|\theta)} \hspace{10pt} (y = 1, 2, \cdots)

の形でゼロおよび正の値の確率を定義します。
ここで \pi = P(Y>0)、つまり \piは、がん検診の例で言えば、検診を一度でも受ける確率を意味します。
まとめると以下のようにも書けます：

\displaystyle P(Y = y) = (1 - \pi) I(y = 0) + \pi \frac{p(y|\theta)}{1 - p(0|\theta)} I(y > 0) \hspace{20pt} (1)

ただし I(y = 0), I(y > 0)は指示関数（カッコの中の論理式が真の場合1、偽の場合0を返す関数のこと）です。

f:id:mstour:20210818201007j:plain

\piと 1 - p(0|\theta)の大小によって、元の確率分布 p(y|\theta)と比較してゼロが過剰か、あるいはゼロが過小かが決まります。
\pi < 1 - p(0|\theta)であればゼロ過剰、 \pi > 1 - p(0|\theta)であればゼロ過小であることを表現することができます。等号が成り立つ場合、元の分布に等しくなります。

正の値のモデリングに使用する確率分布 p(y|\theta)としては、ポアソン分布や負の二項分布のほか、より複雑ないくつかの分布が提案されています。
通常、分散が平均よりも大きい「over dispersion」の場合にはポアソン分布よりも負の二項分布が好まれることが多いですが、ポアソン分布をhurdle model化することによって、ゼロ過剰の場合にはover dispersion、ゼロ過小の場合にはunder dispersionの性質も持つようになります。


zero-inflated model

zero-inflated modelもhurdle modelと同様、ゼロの頻度が非常に多い、つまりゼロの値をとる確率が一般的な確率分布よりも大きいような確率モデルです。
ベースとなるのはPoisson分布のような基本的な離散型分布ですが、hurdle modelとは異なり、切断分布ではなく基本的な離散型分布そのものを利用します。

一般的な定義は以下の通りです。

\displaystyle P(Y = 0) = (1 - \phi) + \phi p(0|\theta), \\ P(Y = y) = \phi p(y|\theta) \hspace{10pt} (y = 1, 2, \cdots)

例えば、比較的耳にすることの多いzero-inflated Poisson modelは、次のように定義されます。

\displaystyle P(Y = 0) = (1 - \phi) + \phi e^{-\mu}, \\ P(Y = y) = \phi \frac{\mu^y e^{-\mu}}{y!} \hspace{10pt} (y = 1, 2, \cdots)

ここで確率 \phiで1、確率 1-\phiで0となる変数 Zを用意すると、上記の確率関数は次のようにまとめられます。

\displaystyle P(Y = y) = (1 - \phi) I(Z = 0) + \phi \frac{\mu^y e^{-\mu}}{y!} I(Z = 1) \hspace{20pt} (2)


このモデルの応用例を考えてみると、理解がしやすいかもしれません。

いま、zero-inflated Poisson modelによってある週の飲酒回数を表現したいものとします。
週の飲酒回数が0だった人たちの集団には、たまたまその週は一度も飲酒をしなかった人と、一切お酒を飲まない人とが混在していると考えられます。
ここで \phiを「飲酒する人の割合（このデータを得るための調査において、飲酒する人が選ばれる確率、ともいえます）」とすると、 Y=0となる確率は「全く飲酒しない人の割合*3（ 1-\phi）」と、「普段飲酒する人が、たまたま週の飲酒回数が0である確率（ \phi e^{-\mu}）」を合計したものと解釈できます。

f:id:mstour:20210818201029j:plain

このように、zero-inflated modelでは「値が偶然ゼロとなる場合」と、「何らかの理由で必然的に値がゼロとなる場合」とを明示的に分けたモデリングになっているといえるでしょう。


回帰モデル

最後に、zero modified dataで表現された変数*4と、それらの値と相関関係のある変数（説明変数）との関係式を構成する回帰モデルについて説明します。
外来の受診の例で言うと、年齢や病歴といった変数が「受診する確率」にも「受診する回数」にも強く関連していることが想像できます。そこで、年齢や病歴を回帰モデルの説明変数とし、それらが「どの程度」受診状況に影響しているかを推測すれば有益な情報が得られるでしょう。

式(1)のhurdle modelに対しては、「正の値になる確率 \pi_i」を例えばロジスティックモデルで、「モデルに使用した離散型分布（例えばポアソン分布）の平均 \mu_i」を対数線形モデルで表します（ iは個人を表すインデックスです）：

\displaystyle \log \left( \frac{\pi_i}{1-\pi_i} \right) = \beta_{10} + \beta_{11} x_{i11} + \cdots + \beta_{1p} x_{i1p}, \\ \log (\mu_i) = \beta_{20} + \beta_{21} x_{i21} + \cdots + \beta_{2q} x_{i2q}

ここで x_{i11}, \cdots, x_{i1p}は正の値になる確率（外来の例だと「受診する確率」）に関係する説明変数、 x_{i21}, \cdots, x_{i2q}は平均値*5（外来の例だと「受診する回数の平均」）に関係する説明変数です。
これらはそれぞれ異なっていても、全く同じでもかまいません。その分野の知識であったり、統計的なモデル選択基準によって決めたりすることになるかと思います。

式(2)のzero-inflated modelについても、全く同様にして回帰モデルを考えることができます。


ただ、いずれの場合も説明変数によって説明される平均パラメータ \mu_iは母集団平均ではないことに注意する必要があります。 \mu_iはzero inflated modelの場合は「正の値を取りうる集団（例えば、何らかの理由で絶対に受診しない人を除いた集団）の平均」、hurdle modelの場合は「その平均に比例する値」に相当するため、分析の目的によっては結果の解釈が難しい可能性があります。

そこで、母集団全体の平均を直接モデル化する方法も提案されています。例えばzero-inflated Poisson modelについては以下の"marginalized zero-inflated Poisson(MZIP) model"が知られています：

\displaystyle \log \left( \frac{\phi_i}{1-\phi_i} \right) = \beta_{10} + \beta_{11} x_{i11} + \cdots + \beta_{1p} x_{i1p}, \\ \log (\nu_i) = \beta_{20} + \beta_{21} x_{i21} + \cdots + \beta_{2q} x_{i2q}

ここで \nu_i = E(Y_i) = \phi_i \mu_iは母集団全体の平均であり、 \mu_iは通常のzero-inflated Poisson modelにおけるPoisson分布のパラメータ、つまり「正の値を取りうる集団での平均」です。
こうすることで、説明変数の母集団平均への影響を直接定量化することができます。


おわりに

今回はゼロの多い（あるいは少ない）離散型データに対する統計モデルとして用いられることのある、hurdle modelとzero-inflated modelについて紹介しました。
StanのUser's Guide(5.6 Zero-Inflated and Hurdle Models | Stan User’s Guide
)でも実行例が載っていますので、また何かのデータを使ってRとStanを用いた分析例も書いていければと思います。



参考文献

[1] Neelon, B., O'Malley, A. J., & Smith, V. A. (2016). Modeling zero‐modified count and semicontinuous data in health services research part 1: background and overview. Statistics in Medicine, 35(27), 5070-5093.
[2] Neelon, B., O'Malley, A. J., & Smith, V. A. (2016). Modeling zero‐modified count and semicontinuous data in health services research part 2: case studies. Statistics in medicine, 35(27), 5094-5112.
[3] 岩崎学, & 大道寺香澄. (2009). ゼロ過剰な確率モデルとそのテスト得点の解析への応用. 行動計量学, 36(1), 25-34.
https://www.jstage.jst.go.jp/article/jbhmk/36/1/36_1_25/_article/-char/ja/
[4] Stan User's Guide : Zero-Inflated and Hurdle Models
https://mc-stan.org/docs/2_20/stan-users-guide/zero-inflated-section.html

*1:逆に、何らかの理由でゼロの頻度が極めて少ない、というケースも考えることができます。

*2:ゼロが多い場合はzero inflatedと呼ばれることが多いですが、ゼロが少ない（zero deflated）場合も含めて「zero modified」と表現されます。

*3:全く飲酒しない人が母集団から選ばれる確率、とした方が適切かもしれません。

*4:回帰モデルでは目的変数、結果変数、応答変数などと呼ばれます。

*5:正確に言うと上記のモデルは「切断分布にする前のオリジナルな離散分布」の平均パラメータ（例えばポアソン分布のパラメータ）に関する関係式を立てており、母集団平均の直接のモデリングにはなっていません。ただ説明変数の値が大きくなると受診回数も増える、といった関係性は知ることができます。後述するように、母集団平均を直接モデリングする方法もあります。

miceパッケージampute関数による欠測データの作成:(1)原理

R 欠測データの解析

はじめに

前回、混合モデルの説明に使用した欠測データの作成のため、Rのパッケージの一つ、miceパッケージ（参考資料1）に実装されている関数の「ampute」（参考資料2）を使用しました。

今回は、ampute関数の原理と使い方をもう少し詳しく見ていきたいと思います。


miceパッケージ

このパッケージは、欠測データの補完方法である「多重代入法(Multiple Imputation)」の一種である、Full Conditional Specification(FCS)法を実行するために用いられます。

元々、多重代入法の理論では、欠測が生じている変数も含めたすべての変数*1の同時確率分布を想定し、その上で欠測のない変数による条件付けのもとで欠測の生じた変数のサンプリングを行うこととされていました。
ところが具体的に同時確率分布を特定することが難しいケースもある*2ことから、補完したい変数一つ一つの「他のすべての変数で条件付けした場合の」確率分布を考えて、変数ごとに補完値を発生させるというFCS法が提案されました。FCS法の代表的なアルゴリズムが、パッケージの名称になっているMICE(Multiple Imputation by Chained Equation)です（参考資料3）。

miceパッケージは主に上記のFCS法によって欠測値を補完するために用いられますが、逆に「欠測を発生させる」という機能もあります。それが、以下で紹介するampute関数です。


一部の値を欠測にさせるampute関数

ampute関数は、データフレームに含まれる任意の変数のうち、一部の値を「NA」に置き換えます。つまり、人工的に欠測を生じさせます。

f:id:mstour:20210711195412j:plain

とりあえずデフォルトの設定通りに欠測を発生させるには、amputeの引数にデータフレームを入れます。返される結果の「amp」に欠測を発生させたデータフレームが格納されます。

# amputeの結果をresultに格納します。
# dataframeはデータフレーム名です。
result = ampute(dataframe)
# 作成された欠測データをmdに格納します。
md = result$amp

ですが、通常は欠測させたい変数、当該変数に欠測が生じる個体*3の割合、欠測パターン*4、欠測メカニズム（MCAR、MAR、MNAR）などを明確に指定したいことが多いため、細かな設定が必要となります。

参考資料4に沿って、ampute関数で用いられている欠測発生の原理を確認していきましょう。


データに欠測値がある場合の統計手法の性能を確認するため*5に、人為的に欠測を発生させたデータを用いてシミュレーションを行うことがあります。
欠測の起こる個体の割合についていくつかの異なるシナリオを考えたいような時には、狙った割合になるようにシミュレーションデータを作成できると嬉しいです。欠測の起こる個体の割合が10%・20%・30%それぞれの場合の解析結果への影響を見積もることで、予定している解析方法を使うことに問題はないかの判断材料が得られるかもしれません。

この時、欠測させる変数の数が1つだけであれば、それほど困難は発生しないでしょう。例えばロジスティック回帰を用いて欠測発生のモデルを作ることにすると、当該変数が欠測する確率が狙った値（例えば30%）になるようにパラメータを調節し、推定された各個体の欠測確率に基づいてデータを欠測させるかどうかを決めれば、おおむね30%の個体に欠測があるデータが得られるはずです。

しかし同様の方法で複数の変数を欠測させる場合、変数ごとの欠測割合をコントロールできても、「少なくとも一つの変数に欠測が生じた個体の割合」のように変数の組み合わせにおける欠測割合をコントロールするのは困難であることが知られています。そこで、複数の変数を同時に欠測させる「Multivariate amputation」というアプローチが考えられています。ampute関数は、この考え方に基づいています。


Multivariate amputation

欠測のある変数が1つだけならば、当然ですが欠測パターンは「当該変数に欠測が生じる」という1通りしかありません。しかし複数の変数に欠測が生じうる場合には、欠測パターンも複数存在します。
例えばA, B, Cという3変数があって、このうちBとCが欠測しうるような場合、欠測パターンは

  • A:欠測なし、B:欠測あり、C:欠測なし
  • A:欠測なし、B:欠測なし、C:欠測あり
  • A:欠測なし、B:欠測あり、C:欠測あり

の3通りが考えられます（すべての変数が「欠測なし」というパターンは除く）*6。
このように欠測しうる変数が複数ある場合、個々の変数ごとに欠測確率のモデル*7を設定するアプローチでは、複数の変数が同時に欠測する割合を思うようにコントロールするのが難しくなります。
そこで、Multivariate amputationでは、「個々の変数」ではなく「起こりうる欠測パターン」ごとに欠測モデルを設定する方針を取ります。

Multivariate amputationは、下記の模式図のように

  1. データセットを「起こりうる欠測パターン」ごとに分割し、
  2. パターンごとの部分データセットにて欠測を人工的に発生させ、
  3. 最後に各部分データセットを結合する、

という手順をとります。

f:id:mstour:20210711195433j:plain
Schouten et al.(2018)をもとに筆者作成

図の左から順に、手順を見ていきましょう。
なお、欠測を生じさせる元のデータセットには欠測がない（完全データ）ものとします。

1. 起こりうる欠測パターンごとにデータセットを分割する

まず、用意したデータセットを、起こりうる欠測パターン*8ごとに分割します。

例として、変数A, B, Cが存在するデータセットにて、以下の3つの欠測パターンを生じさせたい場合を考えましょう。

  • A:欠測なし、B:欠測あり、C:欠測なし　 (1)
  • A:欠測なし、B:欠測なし、C:欠測あり　 (2)
  • A:欠測なし、B:欠測あり、C:欠測あり 　(3)

はじめに、欠測の起こる個体において(1)〜(3)の欠測パターンがそれぞれ何%を占めるかを決めます。この割合をampute関数では「freq」といい、各パターンのfreqの値に応じてデータセットを分割します（すべての変数が欠測なしというパターンは含みません）。
例えば欠測パターン(1)が40%、(2)が40%、(3)が20%を占めるとすると、(1)のパターンには元のデータセットの40%のレコードからなる部分データセットが割り当てられます（2と3も同様）。

2. それぞれの変数が欠測確率へ与える影響の大きさを設定する

続いて、欠測パターンごと（1.で分割した部分データセットごと）に、各変数が欠測へ影響する度合いを設定します。

欠測データ解析の理論では、ある変数が欠測する確率は何らかの変数の値に応じて決まると考えます。例えばMARは、欠測する確率は他の何らかの変数に影響されると想定しており、MNARは欠測した変数自身の値も欠測確率に影響する可能性を考慮に入れます。
そこで、各個体 iの欠測確率が「欠測に関与する変数の値 y」と「その変数の影響度 w」を掛けたものからなる以下の「Weighted sum score」によって決まるものと考えます。

\displaystyle wss_i = w_1 y_{1i} + w_2 y_{2i} + \cdots + w_m y_{mi}

上式の影響度（重み） w_1, \cdots, w_mの設定に基づき、ロジスティックモデルを通して各個体の欠測確率が算出されます*9。次のステップにて、実際に欠測を発生させます。

なお、欠測させたい変数が y_{1i}だとすると、

  • すべての重みが0・・・ y_{1i}の欠測メカニズムはMCAR
  • 重み w_1が0で、他の重みの少なくとも1つは0でない・・・ y_{1i}の欠測メカニズムはMAR
  • 重み w_1が0ではない・・・ y_{1i}の欠測メカニズムはMNAR

という状況に対応します。

各変数の重みは、ampute関数では「weights」により指定します。

3. 指定した欠測の発生割合に基づいて欠測を発生させる

ampute関数では、何らかの変数が欠測する個体の割合を「prop」で指定しておきます。
Weighted sum scoreの算出後、欠測パターンに応じたそれぞれの部分データセットに対して、propで指定した割合の個体に欠測を発生させます。
どの個体に欠測を発生させるかは、Weighted sum scoreの値からロジスティックモデルによって算出した欠測確率に基づき決定されます*10。

最後に、欠測を発生させた部分データセットを統合することで、元のデータセットに欠測を生じさせた新たなデータセットが完成します。


以上のステップによって、複数の変数を対象とする場合にも意図した割合の欠測を容易に発生させることができます。
ではいよいよRでの実践を・・・といきたいところですが、長くなってしまったので、続きは次の記事に回すことにします。


おわりに

欠測を人為的に発生させるための方法である「miceパッケージ・ampute関数」について、まずはどのような原理に基づいているかを紹介しました。
自分で欠測メカニズムのモデルを（例えばロジスティック回帰モデルで）定義するとなると、各変数が欠測確率へ与える影響を表すパラメータの値をうまく調節する必要があります。ampute関数ではそのような複雑な作業をせずとも、全データのうちどの程度に欠測を発生させたいかを直接指定すればよいため*11、とても使い勝手が良いと考えています。

次回は実際にRを動かしてより具体的な話をしていきたいと思います。

今回は以下の資料を参考にしました。
[1] Package ‘mice’ Version 3.13.0.
https://cran.r-project.org/web/packages/mice/mice.pdf
[2] ampute: Generate missing data for simulation purposes.
https://www.rdocumentation.org/packages/mice/versions/3.13.0/topics/ampute
[3] 高井啓二・星野崇宏・野間久史(2016), "欠測データの統計科学", 岩波書店.
[4] Schouten, R. M., Lugtig, P., & Vink, G. (2018). Generating missing values for simulation purposes: a multivariate amputation procedure. Journal of Statistical Computation and Simulation, 88(15), 2909-2930.
https://www.tandfonline.com/doi/full/10.1080/00949655.2018.1491577
[5] Multivariate amputation using ampute.
https://mran.microsoft.com/snapshot/2017-02-20/web/packages/mice/vignettes/ampute.html

*1:ここで「すべて」というのは、「欠測を補完するプロセスにおいて登場するすべての変数」を意味します。例えば個人の識別番号のように、補完の対象とならない・あるいは欠測を説明する役には立たないような変数は含まれません。

*2:すべての変数に正規分布を仮定した場合には同時確率分布も正規分布であることがわかりますが、例えば連続型分布と離散型分布が混ざっているような場合には具体的な同時確率分布を定義することは難しそうです。

*3:以降、解析の単位は「個体」とします。またデータセットには1個体につき1レコードのみ格納されているこものとします。

*4:欠測する変数の組み合わせをまとめたものです。例えば変数A, B, Cが同時に欠測しうる場合、(A, B, C)の組が欠測パターンの1つの要素となります。

*5:例えば、MARではない欠測が起こった場合に、欠測がMARであると仮定する混合効果モデルで解析するとどのくらい結果に悪影響があるか、などを知りたいものとします。

*6:ここでは可能性として考えられるパターンを挙げていますが、人工的に欠測データを作る場合に必ずしもすべてのパターンを含めないといけないわけではありません。また現実のデータでも、必ずしも3通りすべての欠測パターンが存在しているとは限りません。

*7:MCAR以外の欠測メカニズムを考えるには、欠測する個体の割合だけでなく、他の変数が欠測確率に与える影響の大きさや、他の変数と欠測確率とを結びつける関数の形などを特定する必要があります。

*8:人工的に発生させたい欠測パターンのことです。このセクションの最初に挙げた例だと、「Bのみ欠測」「Cのみ欠測」「BとCの両方が欠測」という3パターンに対応する部分データセットがそれぞれ作成されます。

*9:ampute関数ではロジスティックモデルしか実装されていないようですが、モデルの概形（右上がりか右下がりかなど）は「type」にて指定できます。

*10:欠測する個体の割合が意図したものになるように、propで指定した値に応じてロジスティックモデルの位置は調整されます。

*11:とはいえ、その他にもいくつかの設定は必要です。

線形混合モデルにおけるKenward-Roger法：(2)Rによる計算例

R 反復測定データの解析 混合モデル

最終更新：2023/9/10

  • 「実施」セクションの「N=40の欠測なしデータの推定結果」とあるのは「欠測ありデータの推定結果」の間違いでした。修正しました。

はじめに

前回の記事では、線形混合モデルの固定効果に関する推論で使用されるKenward-Roger法の概要を述べていきました。

サンプルサイズが小さい場合、固定効果の分散・共分散を過小に見積もってしまうという問題が知られていたため、補正した推定量を使うことにしようというのがKenward and Roger(1997)の提案でした。
また、固定効果（およびその対比）に関する仮説検定を行う場合に用いる自由度についても、古典的なSatterthwaite法に代わる新たな計算方法が提示されました。

前回は理論的な内容をざっと見るので精一杯でしたので、今回は続編としてRを用いて具体的な計算例を確認していくことにしたいと思います。


今回の流れ

サンプルデータを使用して、Kenward-Roger法がどのような結果を与えるかを実際の数値例で見ていきます。

  1. まずは固定効果の共分散行列について、Kenward-Roger以前の方法（共分散行列を構成するパラメータの推定量を理論的な数式へそのまま代入する）とKenward-Roger法との結果を比較します。
  2. 続いて、自由度の計算結果についてSatterthwaite法とKenward-Roger法それぞれの結果を比較します。

上記の1.と2.を、サンプルサイズが小さい場合（N = 40）と大きい場合（N = 400）、さらに欠測のない場合とある場合とでそれぞれ計算してみます。


サンプルデータと混合モデルの計算に使用するRパッケージ

今回は、2つの治療薬の効果を比較するランダム化比較試験を模したサンプルデータを作成してみます。
データ内の変数の説明は以下の通りです。

  • id : 試験に参加した個人を示す番号です。
  • treat : 治療薬の種類です。前半のidにはA薬、後半のidにはB薬が投与されています*1。
  • Baseline : 治療薬の効果として関心のあるアウトカム指標の、治療開始前の値です。例えば血圧などをイメージしていただけるとよいかと思います。
  • Time : 治療開始後の、アウトカム指標を測定した時点です。今回は2回測定しているものとし、それぞれTime1、Time2としています。
  • y : アウトカム指標の値です。混合モデルによって、Time1、Time2の2回の反復測定データをモデリングします。

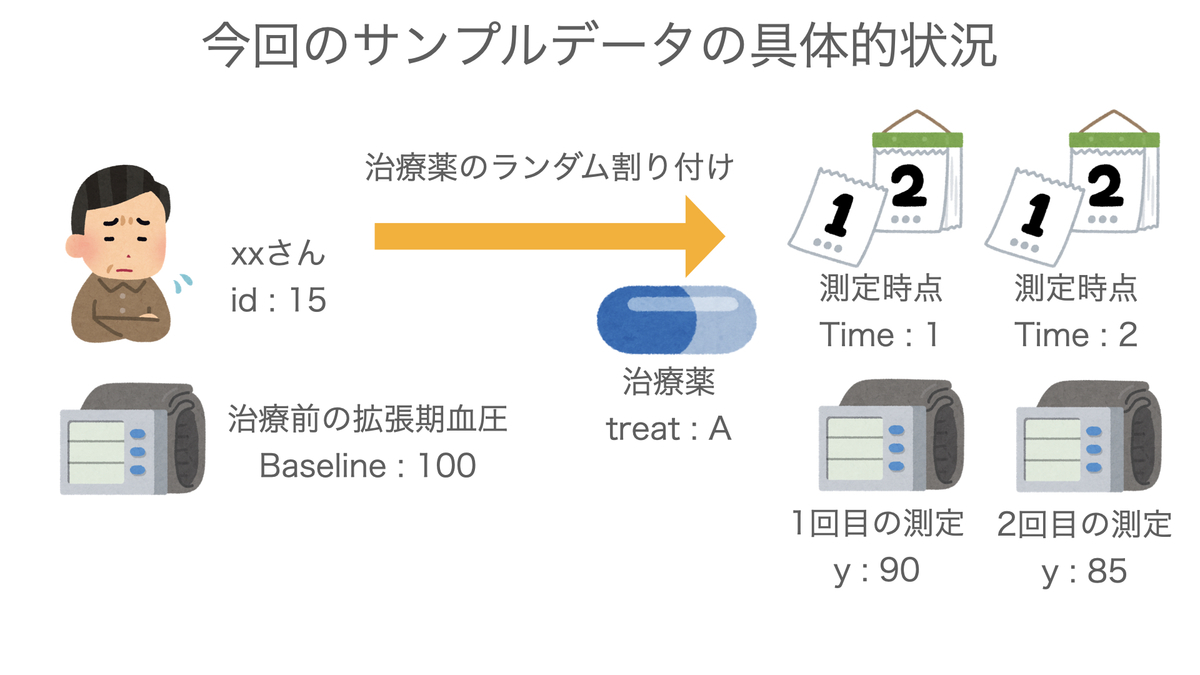
サンプルサイズが小さいパターン（N = 40。A薬・B薬それぞれに20人）のみ、Rのコード例を示します。

# 使用するパッケージを読み込みます。
library(tidyverse)
library(MASS)

# 乱数のシード値と各群のサンプルサイズを定義します。
set.seed(992)
n1 = 20

# アウトカム測定値の共分散行列を定義します。
# 分散は各時点で同じで、共分散はどの時点間でも同じ(Compound symmetry型)とします。
rho = 0.7      # 異なる時点の測定値間の相関
sigma2 = 5      # 測定値の分散
cov = rho * sigma2      # 測定値間の共分散
covm = diag(sigma2, nrow = 3)      # 共分散行列の対角成分
covm[upper.tri(covm) | lower.tri(covm)] = cov      # 非対角成分に共分散を配置して完成 

# アウトカム測定値の平均ベクトルを定義します。
mu_a = c(100, 90, 80)
mu_b = c(100, 95, 95)

# A薬群、B薬群それぞれのアウトカム測定値を多変量正規分布からサンプリングします。
y1_a = round(mvrnorm(n1, mu = mu_a, Sigma = covm), 1)
y1_b = round(mvrnorm(n1, mu = mu_b, Sigma = covm), 1)
# 縦にならべます。
y1 = rbind(y1_a, y1_b)

# idと治療薬
id1 = rep(1:(n1*2))
treat1 = c(rep("A", n1), rep("B", n1))

# データフレームにまとめて、縦型のデータに変形します。
cd1 = data.frame(id = factor(id1), treat = factor(treat1, levels = c("B", "A")),
                 Baseline = y1[, 1], Time1 = y1[, 2], Time2 = y1[, 3]) %>%
  tidyr::pivot_longer(cols = c(Time1, Time2),
                      names_to = "Time", values_to = "y")

以下のようなデータができます。

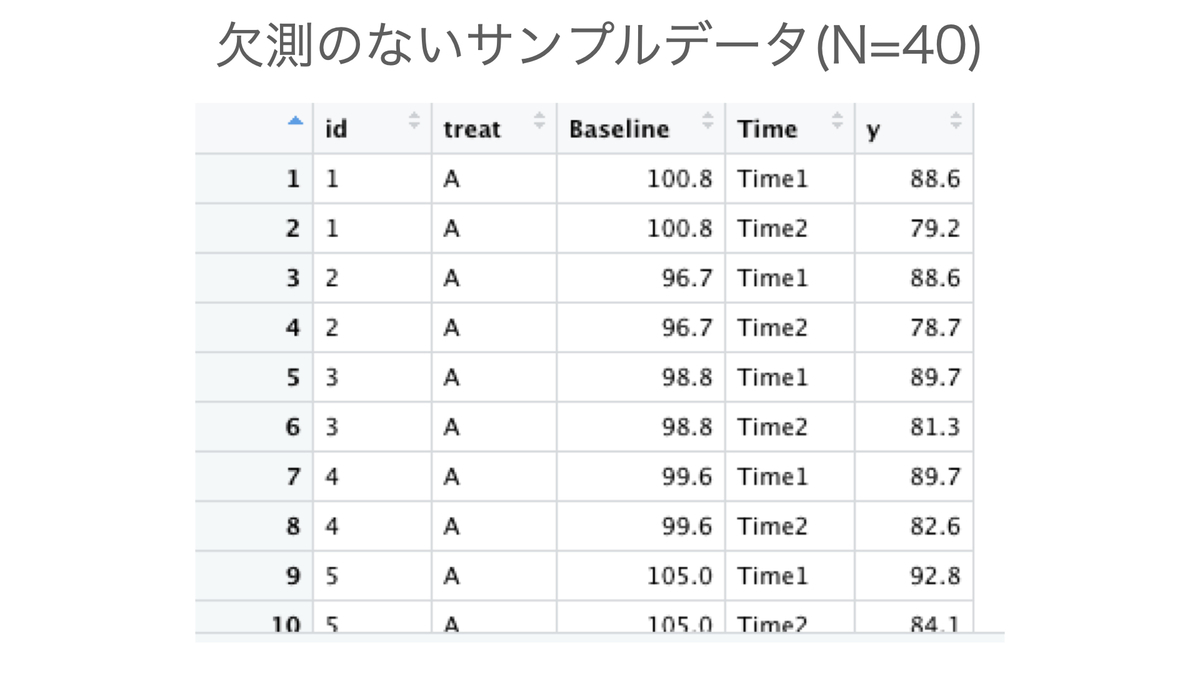
続いて、いくつかのアウトカム測定値が欠測となっているバージョンも作ります。今回は欠測が以前の時点の測定値に依存して起こる、いわゆるMissing at random(MAR)による欠測が一部で生じているような状況を考えます。今回は単純化のため、一度欠測になるとその次の時点も欠測になるようなパターンだけを扱います*2。

データの一部を欠測させるための方法として、今回はmiceパッケージのamputeという関数を使います（参考資料2）。
この関数では、どの変数を欠測させるか、どれくらいの割合で欠測させるか、欠測メカニズムはどのようにするか（MCAR, MAR, MNAR）など細かな指定が可能です。
詳細を書くと本題から外れて長くなってしまうので、次回、amputeを使用した欠測データの作り方の解説を別途していきたいと思います*3。

# miceパッケージを読み込みます。
library(mice)

# 欠測パターンを所定の行列形式で定義します。
# TIme1およびTime2が欠測、Time2のみが欠測という2パターンを定義
patterns = matrix(c(1, 0, 0, 1, 1, 0), nrow = 2, ncol = 3, byrow = TRUE)
rownames(patterns) = c(1, 2)
colnames(patterns) = c("V1", "V2", "V3")

# 各欠測パターンの起こる確率を定義します。
# Time1,2両方欠測する確率は20%, Time2のみ欠測する確率は40%
freq = c(0.2, 0.4)

# 欠測パターンと確率、欠測メカニズムを与えて欠測データを作ります。
y1_amp = ampute(data = y1, freq = freq, patterns = patterns, mech = "MAR")
y1miss = y1_amp$amp

# 完全データと同様にして縦型のデータフレームにまとめます。
md1 = data.frame(id = factor(id1), treat = factor(treat1, levels = c("B", "A")),
                 Baseline = y1miss[, 1], Time1 = y1miss[, 2], Time2 = y1miss[, 3]) %>%
  tidyr::pivot_longer(cols = c(Time1, Time2),
                      names_to = "Time", values_to = "y")

以下のようなデータができました。


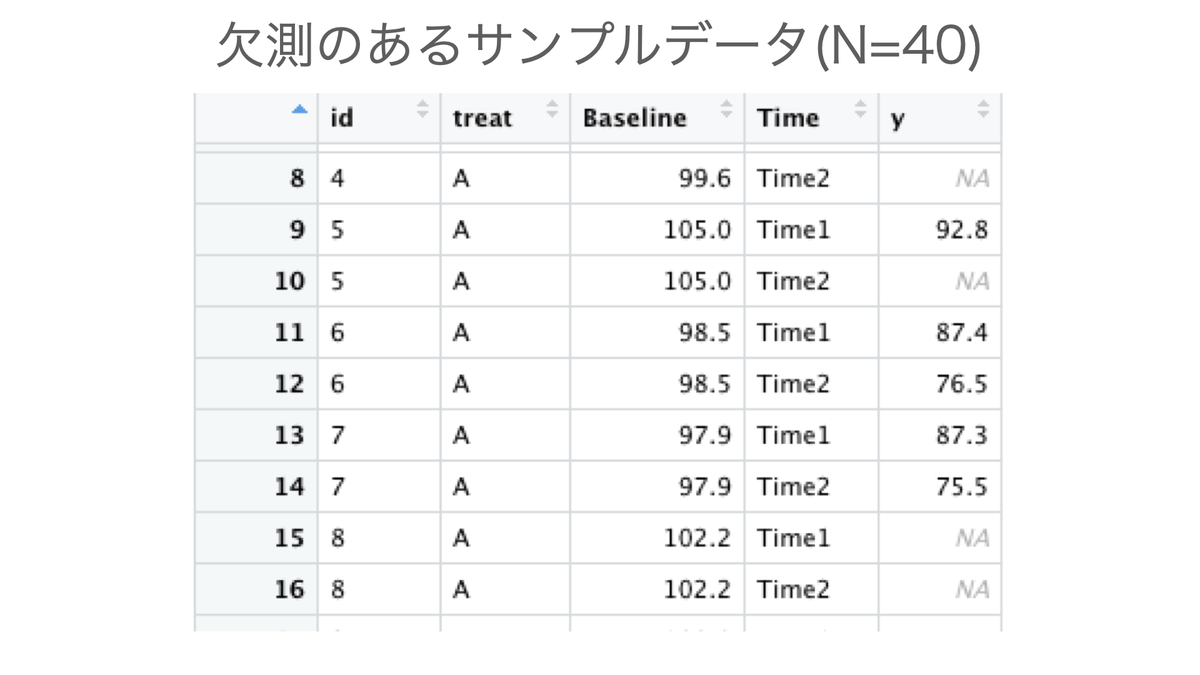
混合モデルの計算には、lme4パッケージを使用します。
ただし、今回はKenward-Roger法による分散推定量および自由度の計算を行うための拡張であるlmerTestパッケージを用いました（参考資料4）。
付随して必要となる、pbkrtestパッケージも合わせてインストールしておきました。


実施

各サンプルデータに対して、以下の混合モデルを当てはめます。
ただし i = 1, \cdots, N(N=40 または400)は個人、 j = 1, 2は治療開始後の測定時点を表すインデックスとします。

\displaystyle y_{ij} = \beta_0 + \beta_1 Treat_i + \beta_2 Time_{ij} + \beta_3 Baseline_i + \beta_4 Treat_i \times Time_{ij} + r_i + \varepsilon_{ij}

  • Treatの値は、個人iの受けた治療がAならば1、Bならば0となります。
  • Timeの値は、時点jがTime1ならば0、Time2ならば1となります。
  • Baselineの値は、個人iの治療開始前の測定値です。

また、 r_iは個人iのランダム効果、 \varepsilon_{ij}は個人iの時点jの測定値に関する誤差で、これらは互いに独立に正規分布に従うものとします。

なお本当は前回の記事とのつながりを考えて、誤差の共分散構造を直接指定するタイプのモデル（Covariance pattern modelやMMRM;Mixed model for repeated mearsureと呼ばれるもの）を用いたかったのですが、lme4では実装されていないようであり、Kenward-Roger法を使用できるRのパッケージは他には見つけられませんでした（参考資料4）。
したがって、誤差の共分散構造をCompound symmetryに指定した場合と同じ結果を与えるランダム効果モデル（切片に個人のランダム効果を設定したもの）を使用することにします。

モデル当てはめのRでのコード例は以下の通りです。

# 必要なパッケージを読み込みます。事前にインストールしてください。
library(lmerTest)
library(pbkrtest)

# cd1_lmerという名前で結果を保存します。
# (1 | id)で、切片に個人のランダム効果を設定します。
cd1_lmer = lmer(y ~ treat + Time + Baseline + treat:Time + (1 | id),
                data = cd1, na.action = na.omit)

# パラメータ推定値などは以下で確認できます。
summary(cd1_lmer)

N=40の欠測ありデータの推定結果のみ、以下に例示します。


さて、まずは固定効果の分散・共分散の推定結果について、Kenward-Roger法による調整を行う場合とそうでない場合とを比べてみます。
vcov関数を用いると調整なしの推定結果、vcovAdj関数を用いると調整を行なった推定結果が出力されます。

vcov(cd1_lmer)

# Kenward-Roger法による調整
vcovAdj(cd1_lmer, details = 0)

N=40、N=400で欠測なしのサンプルデータに対して実行した結果は以下のようになりました。


欠測がない場合には、調整をしてもしなくても変わらない結果になりました*4。

一方、欠測がある場合には若干の結果の違いが見られます。


（推定値の違いが比較的大きい部分に色をつけています）
N=40の場合、パラメータによっては0.02〜0.03程度Kenward-Roger法の方が各固定効果の分散（表の対角線上の値）を大きめに推定していることがありますが、それほど大きな差はなさそうです。特に重要な治療効果の分散（treatAとtreatAが交差する箇所）にはほとんど違いがありません。
異なる固定効果どうしの共分散（対角線以外の部分）については、Kenward-Roger法の方が絶対値が大きく推定されているようです。常にそうなるのかはもう少し調査が必要です。


N=400の場合には、両者の違いはほとんどなくなりました。いずれの推定方法でもサンプルサイズが大きくなれば理論的に真の分散に近づくことが数値的に確認できているかと思います。


次に、自由度の計算および固定効果のF検定について見ていきます。
lmerで推定した結果に対してanova関数を適用し、ddfにそれぞれの方法を記載します。

anova(cd1_lmer, ddf = "Satterthwaite")
anova(cd1_lmer, ddf = "Kenward-Roger")




こちらも、欠測がない場合には自由度の計算結果は全く同じになり、F検定も同じ結果になります。
欠測によってデータがアンバランスになる場合に、違いが現れてきます。

まずはN=40の場合を確認します。


どの変数の効果についても、Kenward-Roger法を用いた方が自由度（F統計量の分母にあたる誤差の自由度。DenDFと表記）は小さい数値になり、各効果がゼロでないことを評価するためのF統計量は小さくなります。つまり、統計的有意になりにくくなっています。


一方で、N=400のサンプルデータでは予想に反して、Kenward-Roger法の方が自由度は少し大きめの値になりました。
欠測はN=40の場合と同じように、各グループ平等に同じ割合で起こるように設定しているので、このような結果になるのは欠測状況の違いによるものではなさそうです。
偶然このようなことが起こるのかもしれません。
しかしながら、N=40の場合と比べると各平方和の値は非常に大きいため、自由度の違いがF値に大きく影響はしていないようです。


今回の実験結果をざっとまとめます。

  • 欠測がないデータの場合、Kenward-Roger法を用いた時と用いない時で結果は変わりませんでした。
  • 欠測があるデータの場合、サンプルサイズが小さめ（今回のN=40の場合）であれば、Kenward-Roger法を用いると固定効果の分散・共分散は多少大きめに推定されました。また、F検定の自由度は若干小さく算出されるため、F統計量は小さくなりました。
  • とはいえ、違いは微々たるものでした。サンプルサイズがもっと小さければ、調整効果は大きくなることが予想されます。
  • サンプルサイズが大きくなると（今回のN=400の場合）、結果に違いはほとんどなくなったと言えます。

おわりに

今回のサンプルデータでは、Kenward-Roger法の使用有無による劇的な違いは見られませんでした。N=40では少しサンプルサイズが大きすぎたかもしれません。
どのような場合に大きな違いが生じるのか、もう少し検討してみる必要があるかと思います。

また、今回は治療グループ間に差があるという状況のサンプルデータを作成したため、Type1 errorが名目の有意水準（例えば両側5%）を超えてしまうかどうかという問題は検討していません。原論文（参考資料1）でも述べられている重要な点であるので、次回以降にこの検討もおこなってみます。

次回は、本題から外れるため詳しくは触れなかった、miceパッケージを用いた欠測データの作成方法を考えていきたいと思います。

今回は以下の資料を参考にしました。
[1] Kenward, M., & Roger, J. (1997). Small Sample Inference for Fixed Effects from Restricted Maximum Likelihood. Biometrics, 53(3), 983-997.
[2] Generate missing values with ampute.
https://www.gerkovink.com/Amputation_with_Ampute/Vignette/ampute.html
[3] Mixed model repeated measures (MMRM) in Stata, SAS and R, The Stats Geek.
https://thestatsgeek.com/2020/12/30/mixed-model-repeated-measures-mmrm-in-stata-sas-and-r/
[4] Kuznetsova, A., Brockhoff, P., & Christensen, R. (2017). lmerTest Package: Tests in Linear Mixed Effects Models. Journal of Statistical Software, 82(13), 1 - 26.
https://www.jstatsoft.org/article/view/v082i13
[5] Bates, D., Mächler, M., Bolker, B., & Walker, S. (2015). Fitting Linear Mixed-Effects Models Using lme4. Journal of Statistical Software, 67(1), 1 - 48.
https://www.jstatsoft.org/article/view/v067i01

*1:ランダム化をするとidはランダムに振られるはずなので現実にはこのような番号づけにはなりませんが、単純化のためこのようなデータの作り方にしています。

*2:例として、薬を飲んでも効果がないように感じられて、途中で臨床試験への参加をやめてしまうような場合などがあります。

*3:実は今回1つごまかしがあって、miceパッケージで実行できる多重代入法の1つMICE法の性質を考えると、Time1で欠測になるかどうかがTime2の情報にも依存するような設定になっているのではないかと思います。経時的にデータをとった場合そのようなことは考えにくいですが、今回はサンプルデータの作り方にこれ以上は触れず、データの一部に欠測があることが混合モデルの計算結果にどう影響するかという点だけを考えることにします。

*4:一部、例えば最後にe-15とかがついている箇所は数値が違いますが、計算方法の違いによるものと思われ、実質的には0です。

線形混合モデルにおけるKenward-Roger法：(1)概要

反復測定データの解析 正規線形モデル 混合モデル

【2021/5/10 追記】
Kenward-Roger法による分散推定量の数式について、より正確な記載に改めました。

はじめに

データどうしの相関を考慮したモデルである混合モデルは、反復測定データの解析などで有効であることが広く知られています。
特に、目的変数の分布として多変量正規分布を想定する線形混合モデル*1が用いられる事例は例えば臨床試験のデータ解析の分野では頻繁に見られます。


実際に線形混合モデルを応用する際には、共分散行列の構造（あるいはランダム効果を置く場所や確率分布）などモデルを特徴づけるいくつかの設定を行うのですが、そのうちの一つに「自由度の計算方法」というものがあります。
ここでいう自由度とは、関心のある固定効果（例えば、介入Aの効果）あるいはそれらの「対比」（例えば、ある時点における介入Aと介入Bとの間の差を表現するのに用います。後述します。）の検定を行う際の、検定統計量が従う確率分布*2の自由度を指します。

反復測定データにありがちな欠測が生じた場合でも、混合モデルを用いれば欠測のある個体のデータも利用してパラメータの推定を行うことが可能ですが、自由度の計算は単純ではなくなることが知られています。
自由度の計算方法の選択肢はいくつかありますが、その中の1つ「Kenward-Roger法」の使用が推奨されることが多くあります（例えば参考資料1）。


今回はこのKenward-Roger法について、少し見ていきましょう。
なお、提案者であるKenward and Rogerの原論文（参考資料2）に沿って話を進めていきますが、非常に難しい内容で細かな部分まで理解しきれない*3ので、実用上知っておくといいかなという程度にかいつまんで説明してみたいと思います。

長くなるので、具体的な数値例などを続編として次回また書きたいと思います。


固定効果の分散が過小に見積もられる問題

今回は、以下の線形混合モデル
\displaystyle \boldsymbol{y} = X \boldsymbol{\beta} + Z \boldsymbol{\gamma} + \boldsymbol{\varepsilon}

を考えます。 \boldsymbol{\beta}は固定効果のベクトル、 \boldsymbol{\gamma}はランダム効果のベクトルです。
このとき目的変数ベクトル \boldsymbol{y}の確率分布は多変量正規分布 N(X \boldsymbol{\beta}, \Sigma)で表すことができます。


通常、固定効果 \boldsymbol{\beta}や共分散行列 \Sigmaに含まれる未知パラメータ*4の推定には制約付き最尤法(Restricted maximum likelihood method; REML)が用いられます。REMLにより推定した共分散行列を \hat{\Sigma}とします*5。以下では話の流れによって「共分散行列」を単に「分散」と言う場合があります。

一方、固定効果を求めるために最適化計算をすると推定量として
\displaystyle (X^T \Sigma^{-1} X)^{-1} X^T \Sigma^{-1} \boldsymbol{y}

が得られますが、未知のパラメータを含む \Sigmaが存在するため、以下のように推定量 \hat{\Sigma}に置き換えたものが固定効果 \boldsymbol{\beta}の推定量として用いられます。
\displaystyle \hat{\boldsymbol{\beta}} = (X^T \hat{\Sigma}^{-1} X)^{-1} X^T \hat{\Sigma}^{-1} \boldsymbol{y}

この \hat{\boldsymbol{\beta}}によって真の値 \boldsymbol{\beta}をバイアスなく推定できることが知られています。


また \hat{\boldsymbol{\beta}}の、サンプルサイズを無限に大きくしたときの（=漸近分布の）分散は
\displaystyle V(\hat{\boldsymbol{\beta}}) \cong (X^T \Sigma^{-1} X)^{-1} \hspace{20pt} (1)

となりますが、やはり未知の \Sigmaが含まれているため、慣習的に \hat{\Sigma}で代用した
\displaystyle \hat{V}(\hat{\boldsymbol{\beta}}) = (X^T \hat{\Sigma}^{-1} X)^{-1} \hspace{20pt} (2)

を分散の推定量として用いてきたようです。
しかしながらこの方法は

  • \hat{\Sigma}のばらつきが考慮されていない（・・・ \hat{\boldsymbol{\beta}}も V(\hat{\boldsymbol{\beta}})も本来は真の分散 \Sigmaを使って算出されるところ、同じ実験を繰り返すと毎回結果が変わる \hat{\Sigma}で代用するため、その分ばらつきが大きくなるはずです）
  • そもそも (X^T \hat{\Sigma}^{-1} X)^{-1}は (X^T \Sigma^{-1} X)^{-1}の不偏な推定量ではない（・・・式(2)では式(1)を正しく推定できていないということでしょう）

ことから、サンプルサイズが小さい場合には \hat{\boldsymbol{\beta}}の分散を小さめに見積もってしまうことが知られていました。

そこで、KenwardとRogerにより、新たな分散推定量が提案されました。


Kenward-Roger法による分散推定量

固定効果推定量 \hat{\boldsymbol{\beta}}の正確な分散（サンプルサイズを無限に大きくしたときに収束する式(1)とは異なる）、以下のように表現できることが知られていました。
\displaystyle V(\hat{\boldsymbol{\beta}}) = (X^T \Sigma^{-1} X)^{-1} + \Lambda \hspace{20pt} (3)

前述のようにサンプルサイズが無限に大きくなると分散は右辺第1項に等しくなりますが、逆に言うとサンプルサイズが小さい場合第1項を用いるだけでは \Lambdaの分ほど分散を過小評価してしまいます。

Kenward-Roger法は、分散の過小評価を防ぐために、前述の式(2)の推定量
\displaystyle \hat{V}(\hat{\boldsymbol{\beta}}) = (X^T \hat{\Sigma}^{-1} X)^{-1}

に、式(3)の \Lambdaに対応する修正項を加えたものを推定量とする方法です。

途中の導出は省略します*6が、式(2)の既存の推定量を \hat{\Phi}とすると


\displaystyle \hat{V}_A(\hat{\boldsymbol{\beta}}) = \hat{\Phi} + 2\hat{\Phi} \left\{ \sum_{i=1}^{r} \sum_{j=1}^{r} W_{ij} (Q_{ij} - P_i \hat{\Phi} P_j - \frac{1}{4}R_{ij}) \right\} \hat{\Phi}

がKenward-Roger法による分散推定量となります。ただし rは共分散行列に含まれる未知パラメータ数で、
\displaystyle P_i = X^T \frac{\partial \Sigma^{-1}}{\partial \sigma_i} X, \\ Q_{ij} = X^T \frac{\partial \Sigma^{-1}}{\partial \sigma_i} \Sigma \frac{\partial \Sigma^{-1}}{\partial \sigma_j} X, \\ W_{ij} = V\left[(\hat{\sigma}_1, \cdots, \hat{\sigma}_r) \right]のi行j列目の要素,

\displaystyle R_{ij} = X^T \Sigma^{-1} \frac{\partial^2 \Sigma}{\partial \sigma_i \partial \sigma_j} \Sigma^{-1} X

です*7。ただし、実際の計算では \Sigmaは \hat{\Sigma}で代用し、 \Sigmaの微分の項は微分した後の結果に各パラメータ \sigma_iの推定量を代入します。

なお共分散構造がパラメータに関して線形である場合、すなわち
\displaystyle \Sigma = \sum_{i=1}^{r} \sigma_i G_i \hspace{20pt} (G_iは適当なn \times n行列)
と表せる場合には、2回微分すると0になるため R_{ij} = 0となり、Kenward-Rogerの分散推定量は次のようになります。

\displaystyle \hat{V}_A(\hat{\boldsymbol{\beta}}) = \hat{\Phi} + 2\hat{\Phi} \left\{ \sum_{i=1}^{r} \sum_{j=1}^{r} W_{ij} (Q_{ij} - P_i \hat{\Phi} P_j) \right\} \hat{\Phi}

例えば、共分散構造がCompound symmetryやUnstructuredの場合にはこれに該当しますが、AR(1)のような構造だと相関パラメータの2乗以上の要素が共分散行列に含まれるため、より一般的な R_{ij}を含む推定量の計算が必要になります（SASではこちらがデフォルトのようです）。

f:id:mstour:20210505094228j:plain

統計ソフトウェアの説明などではKenward-Roger法は「自由度計算方法」として記載されていることが多くみられますが、方法が提案された背景としてまずは分散を過小評価する問題があったようです。


固定効果に関する検定の自由度の計算

モデルの固定効果に関して検定を行う場合、対比(Contrast)を使って考えることが多くあります。
対比とは、固定効果パラメータの線形結合（各パラメータに何らかの係数を掛けて足し算したもの。ただし係数の合計が0になるように制約をつける）のことをいいます。

例えば治療A、B、Cの効果を比較する臨床試験を行い、治療AとBとの比較に関心があるものとします。
統計モデルとして全体平均 \muと、治療A〜Cのそれぞれのアウトカムへの影響を示す固定効果パラメータ \beta_A, \beta_B, \beta_Cの4個の固定効果パラメータを含む線形モデルを用いたものとすると、治療AとBの比較 \beta_A - \beta_Bは
\displaystyle L^T \boldsymbol{\beta} = (0, 1, -1, 0) \left( \begin{array}{c} \mu \\ \beta_A \\ \beta_B \\ \beta_C \end{array} \right) = \beta_A - \beta_B

のように表現できます。 Lは対比の係数からなる行列で、上記のように関心ある比較が1つの場合には単にベクトルになります。
上のように対比を定義すると、治療AとBの間に差がないという帰無仮説 H_0: \beta_A - \beta_B = 0は H_0: L^T \boldsymbol{\beta} = 0と表せます*8。

検定には、Wald 検定と呼ばれる方法が用いられます。
対比を用いて表現すると、帰無仮説 H_0: L^T \boldsymbol{\beta} = 0を検定するための統計量は
\displaystyle F = \frac{(L^T \hat{\boldsymbol{\beta}})^T (L^T \hat{V}(\hat{\boldsymbol{\beta}}) L)^{-1} (L^T \hat{\boldsymbol{\beta}})}{r}

であり、これが自由度 r, \nuのF分布に近似的に従うことを利用します。ただし rは検定の対象となる（仮説として設定する）対比の数であり、これが1つの場合には以下のt統計量
\displaystyle t = \frac{L^T \hat{\boldsymbol{\beta}}}{\sqrt{L^T \hat{V}(\hat{\boldsymbol{\beta}}) L}}

が近似的に自由度 \nuのt分布に従うことを用いて検定することができます*9。
近似分布であるF分布（あるいはt分布）の自由度 \nuは何らかの方法で推定する必要があり、古くからSatterthwaiteにより提案された方法が知られていました。


前置きが長くなりましたが、その自由度の推定方法がKenward-Roger法のもう一つの内容です。
ここまで書いておいて何ですが、自由度推定方法は分散推定量の導出以上に僕の理解できるレベルをはるかに超えているので・・・要点だけ書くと

  • Satterthwaiteの方法で計算に使用する固定効果の分散推定量として、Kenward-Rogerの提案した過小評価を防ぐ推定量を用いる（参考資料4）
  • 複数の対比の場合には非常に複雑な問題になるが、対比の数が1つの時には、Satterthwaiteの方法の単純な修正である（参考資料2）

ということのようです。なお、検定統計量Fやtの計算にもKenward-Roger提案の分散推定量を使用します。

この点は次回、実際にソフトウェアで計算してどのような違いがあるかを見ていくことにします。
原論文を見ると、Kenward-Roger以前の方法だとType1 errorの確率が設定した有意水準を大きく超えるケースがあるようです。


おわりに

Kenward-Roger法について、原論文を片手に概要を紹介していきました。
非常にざっくりとした解説になりましたが、ポイントは以下の2点にまとめられるかと思います。

  • サンプルサイズが小さいときには固定効果の分散を過小推定してしまう危険があるので、それを防ぐための適切な推定量が提案された
  • 固定効果の検定に使用する近似分布の自由度の計算でも、新たに提案した分散推定量を使用することにした

かなり数学的に高度な内容で、今ひとつスッキリと理解できませんが、具体的な計算をしてみるともう少し見えてくることがあるかもしれません。
ということで、次回につづきます・・・。

今回は以下の資料を参考にしました。
[1] 日本製薬工業協会(2016). 欠測のある連続量経時データに対する統計手法について Ver2.0.
http://www.jpma.or.jp/medicine/shinyaku/tiken/allotment/statistics.html
[2] Kenward, M., & Roger, J. (1997). Small Sample Inference for Fixed Effects from Restricted Maximum Likelihood. Biometrics, 53(3), 983-997.
[3] Brown and Prescott(2015). Applied Mixed Models in Medicine. Wiley.
[4] SAS/STAT User's Guide: The MIXED Procedure.
https://documentation.sas.com/doc/en/pgmsascdc/9.4_3.3/statug/statug_mixed_syntax10.htm#statug.mixed.modelstmt_ddfm
https://documentation.sas.com/doc/en/pgmsascdc/9.4_3.3/statug/statug_mixed_details01.htm#statug.mixed.mixedinference
[5] Kuznetsova, A., Brockhoff, P., & Christensen, R. (2017). lmerTest Package: Tests in Linear Mixed Effects Models. Journal of Statistical Software, 82(13), 1 - 26.
https://www.jstatsoft.org/article/view/v082i13

*1:正規(Normal)やガウス(Gaussian)といった言葉を付け加えた方がより正確ですが、「線形混合モデル」で通じることも多いので、煩雑さを避けてこのように記載することにします。

*2:1つの対比についての検定をする場合にはt分布の自由度ですが、より一般の場合（複数の対比の検定）にはF分布の2番目の自由度（分母の自由度）です。

*3:あくまで僕にとってですが・・・

*4:例えば、共分散行列の構造にCompound Symmetry型を仮定する場合には未知パラメータは「各変数で共通の分散」と「すべての変数のペアで共通の共分散」の2つ、Unstructured型の場合には「変数ごとに異なる分散」と「すべての変数ペアごとに異なる共分散」です。

*5:原論文では、共分散行列に含まれるパラメータを \sigma、その推定量を \hat{\sigma}とし、共分散行列自体はそれらに依存するという意味で \Sigma(\sigma)、 \Sigma(\hat{\sigma})と表記しているのですが、ややこしくなるので本文のような表記法とします。

*6:読んでも分からなかったので・・・すみません。

*7:定義自体は書いておかないと何をやっているかイメージがわかないので記載してみましたが、詳細はここでは説明しきれないので、ご関心のある方は原論文やその他解説資料などをあたっていただけると幸いです。

*8:同様にして複数の比較を行うこともできますし、差ではなく固定効果自体が0がどうかの検定を定義することもできます。本題から外れるのでまた別の機会に記事にするかもしれません。

*9:いずれの場合も、データに欠測がないならば近似ではなく正確な分布に従い、 \nuは残差の自由度に等しくなりますが、混合モデルを利用するような場合にはそうでないことの方が多いのではないかと思います。

有意水準と検出力について考えてみよう

R 実験計画法 検定

はじめに

前回の記事では、ランダム化比較試験について架空の事例をもとに考えていきました。

その中で、両側5%の有意水準(Significance level)で検定を行った場合、「本当はグループ間に差がないのに間違って差があると判定する確率は5%になる」という話をしました。
このあたりの説明は本題から逸れるのでかなりすっ飛ばしてしまいましたが...改めて自分なりにまとめるのも良いかも、と思いました。

一方で、サンプルサイズが非常に大きい場合には、グループ間の差がごくわずかであっても差があると判定できてしまう、いわゆる「統計的に有意」と結論できてしまうということもちらっと述べました。
例えば、大変な忍耐を必要とするような勉強法が開発されたとして、それを頑張ってやり遂げると偏差値が1上がることが期待できます、ということが統計的に有意に示されたとしましょう。でも、そんな勉強法を喜んでやる人はいるでしょうか？

f:id:mstour:20210425202346j:plain

本来、検定によってグループ間に差があるかどうかを評価するためには、少なすぎも多すぎもしない適切なサンプルサイズを設定した上で行う必要があります。
この時にカギとなる概念が「検出力(Power)」です。

今回は、有意水準と検出力について、シミュレーション計算も交えてちょっとだけ考えていくことにします。

なお、今回の話はいわゆる「ネイマン・ピアソン(Neyman-Pearson)流の検定」と呼ばれる、我々が学校などで教わることの多い検定方式を前提としています。つまり、否定したい仮説である「帰無仮説(Null hypothesis)」と、帰無仮説と相反する仮説である「対立仮説(Alternative hypothesis)」の2つの仮説を設定し、実験などによって得られたデータからどちらの仮説を採用するかを決定する、という選択問題として検定を考える立場です。
一方で、統計的検定の方法論を最初に確立したフィッシャー(Fisher)の立場はそれとは異なり、対立仮説というものは出てきません。
有意水準や検出力が決定的な意味を持つのは前者のネイマン・ピアソンの考え方で検定を行う場合です*1。

ちょっとややこしい話ですが、統計的有意性やp値に関する混乱の原因の一つとして、検定に関する異なる2つの立場が（多くの場合、明確に意識されることなく）存在していることがあるかと思います。
本題から外れてしまうので、この問題はまたいつか考えることにします。


有意水準と検出力についておさらい

有意水準

検定の手順として、まずは「帰無仮説が本当は正しいのに、間違ってそれを否定する（=対立仮説が正しいと間違って結論づける）」ことを可能な限り避けるように、その確率を適切にコントロールすることを考えます。間違って帰無仮説を否定することを「第一種の過誤(Type1 error)」と呼びます。
「適切にコントロールする」ために、第一種の過誤確率の上限値を設定しておきます。この上限値を有意水準といいます。

なお一般的な検定では、理論的には第一種の過誤確率が有意水準に等しくなるように定義されています*2。
例えば、帰無仮説を H_0、検定に使用する検定統計量(Test statistic)を Tとすると*3、有意水準 \alpha（右辺）と「帰無仮説が本当は正しいのに、間違ってそれを否定する確率」（左辺）は以下のように表現できます：

\displaystyle P(|T| \geq t_{\alpha} | H_0) = \alpha

ここで t_{\alpha}は検定の棄却点(Critical value)といい、通常は検定統計量 Tが従う確率分布*4において、この点よりも大きな値をとる確率が \alpha \times 100%になるような点、という意味で用います。
この点を検定統計量が超えた場合に帰無仮説を否定することになります。確率を表す記号 Pの中の「 | H_0」というのは、「帰無仮説 H_0が正しかった場合に」ということを表す数学的な書き方です。

つまりこの式が意味しているのは、「帰無仮説が正しい時に、（間違って）帰無仮説を否定する確率は \alphaである」と言うことです。上記の式が成り立つためには、 \alphaの値が変わる時には t_{\alpha}の値も同時に変更する必要があります。

よく言われる「有意水準5%」とは、上の式に出てくる \alphaを0.05と設定したものです*5。
しつこいようですが、有意水準5%の検定とは、「帰無仮説が本当は正しいのに、間違ってそれを否定する確率が5%であるような検定」ということになります。

検出力

検出力は、一言でいうと「正しく帰無仮説を否定できる確率」のことを指します。
逆に言うと、1から検出力を引いたものは「正しく帰無仮説を否定できない確率」、つまり「間違って対立仮説を採用する確率」を意味します。この「正しく帰無仮説を否定できない（=間違って対立仮説を採用する）」という事象は「第二種の過誤(Type2 error)」と呼ばれます。
第二種の過誤を起こす確率は \betaで表すことが多く、その場合検出力は 1 - \betaで表されます。

f:id:mstour:20210425202414j:plain

おおざっぱに言うと上記の通りなのですが、検出力は有意水準とは異なる点があります。
有意水準は、あらかじめ5%などの値に固定することが検定の大前提です。一方、検出力とは、正確に言うと「有意水準が \alphaで、サンプルサイズが Nで、データのばらつきが \sigmaで、（2グループ間の比較の場合）グループ間の真の差が \Delta \neq 0（つまり、グループ間に差がない、という帰無仮説は間違い）である場合に、何%の確率で正しく帰無仮説を否定することができるか」を表しています。
したがって、帰無仮説を否定できる（=いわゆる「有意差がある」と判断する）確率は以下のファクターに影響を受けます。

  1. 有意水準 \alpha
  2. サンプルサイズ N
  3. データのばらつき \sigma
  4. （グループ間の比較を行う場合）グループ間の真の差 \Delta

有意水準が大きくなる（第一種の過誤確率が高くなる、基準の甘い判定）と、帰無仮説を否定しやすくなるため検出力は上がります。
またサンプルサイズが大きくなると、推定のばらつきが小さくなることを通して、検出力が高くなります。データのばらつきが小さいことも、推定のばらつきが小さくなることに直結するので同様です。
さらにグループ間の差が大きければ大きいほど、帰無仮説に反する結果を得やすくなるため、やはり検出力が高くなります。

つまり、真の差が同じでも、サンプルサイズが大きくなれば検出力が上がり、帰無仮説を否定しやすくなるなるわけです。
極端な話、冒頭で述べたような偏差値を1だけ上げるような勉強法があったとすると、実用上の意味に乏しくてもサンプルサイズを増やしさえすれば、効果がないという帰無仮説を否定し、いわゆる「統計的に有意」という主張ができてしまうことになります。

このような問題があるため、検定で仮説を検証しようとする時には、本当に意味のある差がある場合だけ「統計的に有意」と判定できるよう、事前に「サンプルサイズ計算」を行うことが非常に重要になります。
むしろ適切なサンプルサイズ計算が行われていないような場合には、不用意に検定を行うべきではないと考えた方が良いかもしれません*6。


シミュレーションで理解する

検出力について、より具体的にシミュレーション実験で確認してみましょう。
前回の記事と同じように、ある設定のもとでデータを生成し、検定を行うというプロセスを反復します。
検出力は「正しく帰無仮説を否定できる確率」なので、反復回数を1000回とすると、1000回中何回帰無仮説を否定するという結論になったかを見れば理論的な値に近い数値が得られることが期待できます*7。

冒頭の話を踏まえ、今回は勉強法Aを実施したグループ（グループA）と勉強法Bを実施したグループ（グループB）の「偏差値」の平均*8の差を検定するという場面を想定してみます*9。

まずは前準備を行っておきます。

library(tidyverse)
library(gtsummary)

set.seed(1234)
nsim = 1000

mean_a = 50
mean_b = 45
mean_c = 49
sd = 10
  • 1番目のブロック：使用するパッケージを読み込みます。データフレーム加工のためにtidyverse、結果の要約にgtsummaryを使用しました。
  • 2番目のブロック：乱数のシード値と、シミュレーション回数(1000回に設定)です。
  • 3番目のブロック：mean_aはグループAの平均、mean_bとmean_cはグループBの平均です（いくつかのパターンでシミュレーションするため、2通りの値を用意しました）。またsdは両グループの標準偏差*10です。

シミュレーション・パターン1

最初に、「狙った検出力を出せるようにサンプルサイズの計算を事前に行った」という想定でやってみます。
例えば、グループAとBの差が5、標準偏差が10であると見込まれる時に両側5%の有意水準で検定を行うと、検出力80%を達成するにはサンプルサイズはいくつ必要か？を事前に計算しておき、算出されたサンプルサイズのデータを得るような実験を計画した、という場面を想定します。

diff = mean_a - mean_b
power.t.test(delta = diff, sd = sd, power = 0.80, sig.level = 0.05,
             alternative = "two.sided", type = "two.sample")

上記のようにすると、この設定で必要なサンプルサイズが計算できます。詳しいことはまた別の機会に記事にしようと思いますので、ここでは計算結果のみ以下に示します。

     Two-sample t test power calculation 

              n = 63.76576
          delta = 5
             sd = 10
      sig.level = 0.05
          power = 0.8
    alternative = two.sided

NOTE: n is number in *each* group

計算の結果、各グループのサンプルサイズとして63.77必要なことがわかりました。
検出力が期待する値を下回ることのないように、通常は小数点以下を切り上げた値を採用します。
したがって、シミュレーション・パターン1では、各グループの人数が64人になるように実験を計画した、という設定にします。

シミュレーションは以下のコードにより行いました。

# シミュレーション1
npergroup1 = 64
pvalue1 = NULL
for (i in 1:nsim){
  group = c(rep("A", npergroup1), c(rep("B", npergroup1)))
  val_a = rnorm(n = npergroup1, mean = mean_a, sd = sd)
  val_b = rnorm(n = npergroup1, mean = mean_b, sd = sd)
  val = c(val_a, val_b)
  simdata = data.frame(group = factor(group), val = val)
  
  ttest = t.test(val ~ group, data = simdata, var.equal = TRUE)
  pvalue1 = c(pvalue1, ttest$p.value)
}

result_df1 = data.frame(pvalue = pvalue1) %>%
  mutate(reject = case_when(
    pvalue < 0.05 ~ 1,
    TRUE ~ 0)
  )
  • for内の1番目のブロック：正規分布に従う乱数を用いて模擬データを生成しています。先のサンプルサイズ計算で想定した通りにグループAの平均が50、グループBの平均が45、標準偏差が両グループともに10となるようにしました。
  • for内の2番目のブロック：2グループ間の平均差についてt検定を行い、p値を計算しています。
  • for後のブロック：1000回の結果のうち、p値が0.05未満だったものに1をつけます。

結果はgtsummaryを用いて以下のようにまとめました。計算の過程で使ったp値についても、おまけとして中央値と最小値・最大値を載せました。

tbl_summary(result_df1,
            type = list(reject ~ "continuous"),
            statistic = list(pvalue ~ "{median}[{min}, {max}]",
                             reject ~ "{mean}"),
            digits = list(pvalue ~ 4,
                          reject ~ 2),
            label = list(pvalue ~ "p-Value",
                         reject ~ "Power")
            ) %>%
  modify_header(
    update = list(
      label ~ "",
      stat_0 ~ "**Simulation1 : Delta=5, N = 64**"
    )
  )

シミュレーション結果は以下のようになりました。

f:id:mstour:20210425202434j:plain

「Power」の欄に、p値が0.05未満になった割合(=両側有意水準5%で検定した時に帰無仮説を否定できた割合)を示しました。これがシミュレーションから推定される検出力を表しています。
検出力が80%になるように計算されたサンプルサイズで実験を行った場合、期待通りの検出力が確保できそうだということが分かります。
「p-Value」の欄を見ると、p値の中央値は0.0069と小さな値となっていますが、最大値は0.9358であり非常に大きな値が出ることもありました。実際、2グループに差があるような場合、p値は右側に裾の長い分布を示すことが知られています。

シミュレーション・パターン2

次に、各グループの平均・標準偏差は同じだが、サンプルサイズを各グループ2000に増やした場合をやってみます。サンプルサイズが増えれば検出力は高くなるはずです。
コードはほぼ同様です。

# シミュレーション2
npergroup2 = 2000
pvalue2 = NULL
for (i in 1:nsim){
  group = c(rep("A", npergroup2), c(rep("B", npergroup2)))
  val_a = rnorm(n = npergroup2, mean = mean_a, sd = sd)
  val_b = rnorm(n = npergroup2, mean = mean_b, sd = sd)
  val = c(val_a, val_b)
  simdata = data.frame(group = factor(group), val = val)

  ttest = t.test(val ~ group, data = simdata, var.equal = TRUE)
  pvalue2 = c(pvalue2, ttest$p.value)
}

result_df2 = data.frame(pvalue = pvalue2) %>%
  mutate(reject = case_when(
    pvalue < 0.05 ~ 1,
    TRUE ~ 0)
  )

tbl_summary(result_df2,
            type = list(reject ~ "continuous"),
            statistic = list(pvalue ~ "{median}[{min}, {max}]",
                             reject ~ "{mean}"),
            digits = list(pvalue ~ 4,
                          reject ~ 2),
            label = list(pvalue ~ "p-Value",
                         reject ~ "Power")
            ) %>%
  modify_header(
    update = list(
      label ~ "",
      stat_0 ~ "**Simulation2 : Delta=5, N = 2000**"
    )
  )

f:id:mstour:20210425202449j:plain

予想通り検出力は非常に高くなり、1000回のシミュレーションの全てで帰無仮説を否定できる結果になりました。
ではサンプルサイズを増やしさえすればよいかと言うと、そうとも限らない問題があります。

シミュレーション・パターン3

今度は、サンプルサイズをシミュレーション・パターン2と同じく各グループ2000とし、グループAの平均を50、グループBの平均を49に設定してみます（標準偏差はこれまでと同様に各グループで10）。
2グループの平均の差は1であり、当初よりかなり小さい設定です。

# シミュレーション3
npergroup3 = 2000
pvalue3 = NULL
for (i in 1:nsim){
  group = c(rep("A", npergroup3), c(rep("B", npergroup3)))
  val_a = rnorm(n = npergroup3, mean = mean_a, sd = sd)
  val_b = rnorm(n = npergroup3, mean = mean_c, sd = sd)
  val = c(val_a, val_b)
  simdata = data.frame(group = factor(group), val = val)
  
  ttest = t.test(val ~ group, data = simdata, var.equal = TRUE)
  pvalue3 = c(pvalue3, ttest$p.value)
}

result_df3 = data.frame(pvalue = pvalue3) %>%
  mutate(reject = case_when(
    pvalue < 0.05 ~ 1,
    TRUE ~ 0)
  )

tbl_summary(result_df3,
            type = list(reject ~ "continuous"),
            statistic = list(pvalue ~ "{median}[{min}, {max}]",
                             reject ~ "{mean}"),
            digits = list(pvalue ~ 4,
                          reject ~ 2),
            label = list(pvalue ~ "p-Value",
                         reject ~ "Power")
) %>%
  modify_header(
    update = list(
      label ~ "",
      stat_0 ~ "**Simulation3 : Delta=1, N = 2000**"
    )
  )

f:id:mstour:20210425202503j:plain

検出力の推定値は0.87であり、かなりの確率で帰無仮説が否定されることになります。

繰り返しになりますが、このように必要以上にサンプルサイズが増えすぎると、実用上あまり意味がないような差であっても「統計的に有意」と判定する可能性が高くなります。


おわりに

検定にまつわる話は、個人的な感覚ですが、統計モデリングの手法と比べて正しい理解がなかなか難しいように思います（私自身そうです）。
また誤用や解釈に関する議論の最も多いトピックの1つであることは間違いありません。
少なくとも、検定やp値「だけ」で何かを判断しようとしないようにするのが無難な態度ではないか、と考えています。

今回の記事は以下の資料を参考にしました。
[1] Gibson E.W.(2021) "The Role of p-Values in Judging the Strength of Evidence and Realistic Replication Expectations", Statistics in Biopharmaceutical Research, 13, 6-18.
https://www.tandfonline.com/doi/full/10.1080/19466315.2020.1724560
[2] 柳川尭(2017) "p値は臨床研究データ解析結果報告に有用な優れたモノサシである", 計量生物学, 38, 153-161.
https://www.jstage.jst.go.jp/article/jjb/38/2/38_153/_pdf
[3] 汪金芳, 桜井裕仁(2011), "ブートストラップ入門", 共立出版.
[4] John M. Lachin(2020), "医薬データのための統計解析", 共立出版.

*1:後で書くように、有意水準が「間違って対立仮説を選択する確率」、検出力が「正しく対立仮説を選択する確率」に対応します。フィッシャーの立場でも有意水準は考えますが、検出力という概念はありません。

*2:理論的にはそうなのですが、必要な仮定を満たしていない等の状況によって第一種の過誤確率は設定した有意水準より大きくなったり小さくなったりします。

*3:例えば2グループの平均に関するt検定であれば、2グループの平均の差をその標準誤差で割ったものが Tに相当します。

*4:t検定の場合は、t分布です。

*5:ここでは一般的に使用されることの多い両側検定を考えています。片側検定の場合は |T|の絶対値を取らず、しかるべき方向の不等号を設定すれば同様に有意水準が定義されます。

*6:ただし、フィッシャー流の考え方に基づく検定に関してはこの限りではありません。この話題については例えば参考資料[2]をご覧ください。

*7:無限にシミュレーションを繰り返せば、理論的な値に収束します。

*8:得られたデータから計算される「標本平均」ではなく、データの背後に想定する確率分布の「真の平均」を意味しています。文章が煩雑になるので「真の平均」を単に平均と書くことにします。

*9:なんらかの具体的な状況設定があった方がわかりやすいので例として出しましたが、このような検討に実用上の意味があるかはここでは考えないことにします。

*10:これもデータから計算される値ではなく、確率分布が持つ真の値を意図しています。

シミュレーションで理解するランダム化比較試験：(2)処置の効果を正しく推定するために

実験計画法 R

はじめに

前回は、異なる処置をランダムに割り当てれば、処置のグループ間で対象者の属性が偏らずにバランスするというお話をしました。
mstour.hatenablog.com
具体的には、内容の異なるクーポンAとクーポンBのどちらがより売り上げの増加につながるかを検討するという事例を考えました。ランダム化をしない場合・した場合それぞれでクーポンAを配布されたグループ（以下、グループAとします）とクーポンBを配布されたグループ（同じくグループBとします）の属性を集計し、ランダム化をしない場合には属性がグループ間でアンバランスになりうること、対してランダム化によってうまく属性のバランスが取れそうだということを確認しました。

今回は、ユーザーのある属性がクーポン配布後の購入金額に強く影響を及ぼすようなケースを考え、ランダム化を行わないと処置（クーポン）の効果を誤って推定してしまう恐れがあることをシミュレーションで見ていきたいと思います。


設定

前回と同じく、異なる内容のクーポンAとクーポンBのどちらがより購入金額を増加させるかを調べたいという架空の事例で説明していきます*1。状況設定を再掲すると以下の通りです。

＊　＊　＊
とあるアパレルショップでは、新規にアプリ会員登録をしたお客さんを対象に、次回の来店時に使用できるクーポンを配布することにしました。ただし、クーポンの内容をどうするかについては社内で議論があり、以下の2つのどちらが次回の購入金額アップにつながるかを確かめたいということになりました。

(クーポンA)：5,000円以上の買い物をした場合に1,000円を割引
(クーポンB)：10,000円以上の買い物をした場合に購入金額の10%を割引

さらに、一度の購入単価はお客さんの属性（年齢、性別、収入、など・・・）によってかなり違いそうだという意見が出たため、どちらのクーポンを配布するかをランダムに決めることでクーポンA/Bそれぞれの配布されるお客さんの属性が偏らないよう配慮し、平均的にどちらのクーポンを配布したグループの売り上げが高くなるかを評価しよう、と会議で決定しました。
＊　＊　＊

今回は、グループAとグループBの次回の購入金額を比較するという状況を考えます。

さて、もう少し詳しく設定を作っていきましょう。
まず、購入金額は女性の方が男性よりも平均で5,000円ほど大きい傾向にあるものとします。したがって、今回のシミュレーションでも購入金額のデータ生成にはそのことを反映させます。また、話を単純にするために、それ以外の属性は全く購入金額には影響していないものとします。
もう一つ重要な点として、クーポンAとクーポンBには効果の違いはないものとします。したがって、正しく推定を行うことができれば、グループAとグループBの購入金額の平均は同じくらいになるはずです。

そして、前回と同じく「ランダム化を行わないケース」「ランダム化を行うケース」それぞれで結果がどうなるかを見ていくことにします。
割り当て方法1として前半の500人にクーポンA、後半の500人にクーポンBを配布するという安直な方法を、割り当て方法2としてランダムにどちらのクーポンを配布するかを決める方法を設定します。

今回のポイントは、「処置（A/B異なるクーポンの配布）はアウトカム（購入金額）には影響を与えないが」、「処置以外の因子（性別）はアウトカム（購入金額）に影響を与える」という点です。
したがって、もしクーポンの割り当てと性別とに関連性があった場合には「交絡」が生じ、クーポンの違いと購入金額との間に見せかけの関連性が現れてしまいます。

f:id:mstour:20210411211416j:plain

この点を、ランダム化をしない場合（割り当て方法1）とランダム化した場合（割り当て方法2）との対比で確認していきましょう。


シミュレーション

前回と同じ要領で乱数を利用して模擬データを作っていきますが、今回は「同じ模擬データ生成プロセスを1000回繰り返す」ということを行います。
つまり、もしもクーポン配布の実験を同じ条件で1000回繰り返したとするとどうなるのか、を見ていきます。1回だけの結果は偶然に左右される恐れがありますが、大量の反復結果を平均することで真の状況に近い結果を得ることが期待できます。


まずはシミュレーションのコード全体を掲載します：

# 使用するパッケージ
library(tidyverse)
library(TruncatedNormal)
library(gt)

# 設定
n = 1000
set.seed(1234)
nsim = 1000

# 各回の結果を格納する入れ物
result1 = NULL
result2 = NULL
test = NULL

# シミュレーション
for (i in 1:nsim){
  # 割り当て方法1
  alloc1 = c(rep("A", n/2), rep("B", n/2))
  # 割り当て方法2
  alloc2 = sample(alloc1)
  # 性別
  gender = c(rbinom(n/2, 1, 0.7), rbinom(n/2, 1, 0.3))
  # 購入金額
  buy = round(rtnorm(n = n, mu = 15000, sd = 5000, lb = 3000, ub = 50000))
  buy[gender == 1] = buy[gender == 1] + 5000 # 女性の場合平均5,000円高い
  # データフレーム
  simdata = data.frame(alloc1 = factor(alloc1),
                       alloc2 = factor(alloc2),
                       gender = gender,
                       buy = buy) %>%
    mutate(genderc = factor(case_when(
      gender == 1 ~ "F",
      gender == 0 ~ "M"
    )))
  # 割り当て方法1の集計
  summary1 = group_by(simdata, alloc1) %>%
    summarize(buy_mean = mean(buy), female_prop = mean(gender)) %>%
    mutate(simno = i)
  # 割り当て方法2の集計
  summary2 = group_by(simdata, alloc2) %>%
    summarize(buy_mean = mean(buy), female_prop = mean(gender)) %>%
    mutate(simno = i)
  # t検定と95%信頼区間
  test1 = t.test(buy ~ alloc1, data = simdata, var.equal = TRUE)
  test2 = t.test(buy ~ alloc2, data = simdata, var.equal = TRUE)
  testres = data.frame(allocation = c(1, 2),
                       pvalue = c(test1$p.value, test2$p.value),
                       CIlower = c(test1$conf.int[1], test2$conf.int[1]),
                       CIupper = c(test1$conf.int[2], test2$conf.int[2]))
  # 結果を格納
  result1 = rbind(result1, summary1)
  result2 = rbind(result2, summary2)
  test = rbind(test, testres)
}

ざっくりと、中身を部分に分けて説明していきます。

library(tidyverse)
library(TruncatedNormal)
library(gt)

n = 1000
set.seed(1234)
nsim = 1000

今回使用するパッケージの読み込みと、シミュレーションの設定です。クーポンを配布するユーザーは合計1000人、シミュレーションの反復回数は1000回にしています。また乱数のシード値を指定することで同じ結果が再現できるようにしています。

result1 = NULL
result2 = NULL
test = NULL

これらにシミュレーションの各回の結果を格納していきます。

for (i in 1:nsim){

}

シミュレーションのためのfor文（反復処理）です。Rでfor文は処理速度がとても遅いらしく推奨されていないようなのですが、直感的に理解しやすいので今回はこれで実施しています*2。
以下は、シミュレーションの各ステップの内容（for文の中身）です。

alloc1 = c(rep("A", n/2), rep("B", n/2))
alloc2 = sample(alloc1)
gender = c(rbinom(n/2, 1, 0.7), rbinom(n/2, 1, 0.3))
buy = round(rtnorm(n = n, mu = 15000, sd = 5000, lb = 3000, ub = 50000))
buy[gender == 1] = buy[gender == 1] + 5000

割り当て方法は、「設定」のところで記述した通りです。性別は前回と同じ方法でサンプリングします。つまり、前半の500人には女性が、後半の500人には男性が多くなります。
クーポン配布後の購入金額については最小3000円・最大50000円となるように切断正規分布からサンプリングしますが、女性のほうが平均的に5000円購入金額が高いという設定を行いました。
さらに、購入金額は配布されたクーポンがAかBかには関係なくサンプリングされています。クーポンAとBとの間には差がないという状況にするため、このように設定しています。

続いて上記で作成した変数をデータフレームの形にまとめます。

simdata = data.frame(alloc1 = factor(alloc1),
                       alloc2 = factor(alloc2),
                       gender = gender,
                       buy = buy) %>%
mutate(genderc = factor(case_when(
      gender == 1 ~ "F",
      gender == 0 ~ "M"
)))


以下のコードでは、割り当て方法1の場合・2の場合それぞれで、グループA/Bそれぞれの女性の割合と購入金額の平均値を集計します。
また、各割り当て方法でグループA/B間の購入金額の差に関するt検定のp値と、95%信頼区間を計算します*3。
最後にこれらの結果を格納して、次の回へ進みます。

  # 割り当て方法1の集計
  summary1 = group_by(simdata, alloc1) %>%
    summarize(buy_mean = mean(buy), female_prop = mean(gender)) %>%
    mutate(simno = i)
  # 割り当て方法2の集計
  summary2 = group_by(simdata, alloc2) %>%
    summarize(buy_mean = mean(buy), female_prop = mean(gender)) %>%
    mutate(simno = i)
  # t検定と95%信頼区間
  test1 = t.test(buy ~ alloc1, data = simdata, var.equal = TRUE)
  test2 = t.test(buy ~ alloc2, data = simdata, var.equal = TRUE)
  testres = data.frame(allocation = c(1, 2),
                       pvalue = c(test1$p.value, test2$p.value),
                       CIlower = c(test1$conf.int[1], test2$conf.int[1]),
                       CIupper = c(test1$conf.int[2], test2$conf.int[2]))
  # 結果を格納
  result1 = rbind(result1, summary1)
  result2 = rbind(result2, summary2)
  test = rbind(test, testres)

結果

結果の出力にはgtパッケージを使ってみることにしました。
例えば以下のページが非常に参考になりました。
onoshima.github.io


まず、割り当て方法1を行った場合の集計結果は次のようになりました。

f:id:mstour:20210411211441j:plain

一番右の列「Female(Percent)」は、女性の割合の1000回のシミュレーション結果を平均したものです*4。
グループAには女性が、グループBには男性が多く含まれていることがわかります（そのようにデータを作っているのですが）。
真ん中の列「Buy(Yen)」が、クーポン配布後の購入金額の全シミュレーションを通した平均を示しています。グループAの方がグループBよりも2000円ほど高くなっています。
本当はクーポンAとクーポンBとで購入金額に差はないのですが、テキトウにクーポンの配布を行うと間違ってクーポンAの方が売り上げアップにつながると結論してしまう可能性があることがわかります。


次に、割り当て方法2（ランダム化）の場合の集計結果は以下のようになりました。

f:id:mstour:20210411211453j:plain

同じく1000回のシミュレーションを通した平均を示していますが、グループAとBの間には違いはほとんどありません。
もちろん、偶然グループAとBの間に差が生じる可能性はありますが、ランダムにクーポンを配布すれば、クーポンの効果を間違って結論づけてしまう危険はかなり避けられると言えるでしょう。
この点は、t検定のp値と95%信頼区間の結果を見るとより理解できます。

f:id:mstour:20210411211505j:plain

左の列「Method」は、割り当て方法1（ランダム化なし）と2（ランダム化）を示しています。

真ん中の列「Type1 error rate」には、1000回のシミュレーションのうち、t検定のp値が0.05未満になった割合を計算したものです。
割り当て方法1のType1 error rateは100%であり、これは1000回中1000回でp<0.05となったことを意味します。本当はグループ間に差はないはずなので、有意水準5%でt検定を行った場合に確実に間違って有意差ありと判定してしまいます*5。
一方、割り当て方法2のType1 error rateは5.5%であり、有意水準5%に近い値となっています。この結果は、有意水準を5%とした場合の「本当は差がないのに、間違って差があると結論づける確率が5%」という検定の前提条件に整合しており、割り当て方法1のような重大な問題が起こっていないことがわかります。

右の列「Coverage probability」は、シミュレーションで計算した1000個の95%信頼区間のうち、本当のグループ間の差である「0」を含んでいるものの割合を算出したものです（日本語では、「被覆確率」と呼ばれます）。
割り当て方法1では、0を含む信頼区間は一つもありませんでした。正しく推定が行われていたならば、計算した信頼区間のうち95%は0を含むことが期待されるので、やはり割り当て方法1には欠陥があることがわかります。
割り当て方法2では、Coverage probabilityは94.5%であり、期待される95%にほぼ等しい結果になりました。

集計に使用したRのコードは以下の通りです。長くなりますので、記法の詳細については前述の参考資料などをご覧いただけると幸いです。

simall_1 %>%
  dplyr::select(-female_mean_all) %>%
  gt() %>%
  fmt_number(columns = vars("buy_mean_all", "female_pct"), decimals = 1) %>%
  cols_label(alloc1 = "Group", buy_mean_all = "Buy(Yen)", female_pct = "Female(Percent)")
simall_2 %>%
  dplyr::select(-female_mean_all) %>%
  gt() %>%
  fmt_number(columns = vars("buy_mean_all", "female_pct"), decimals = 1) %>%
  cols_label(alloc2 = "Group", buy_mean_all = "Buy(Yen)", female_pct = "Female(Percent)")
testall_sum %>%
  gt() %>%
  cols_label(allocation = "Method", alpha_error = "Type1 error rate", coverage = "Coverage probability")

まとめ

関心のある結果（購入金額）に影響を与える因子（性別）によって処置（異なるクーポンの配布）に見せかけの効果が現れるような状況を想定し、ランダム化をしない場合・した場合それぞれでどのようなことが起こるかをシミュレーションで見ていきました。
ランダム化を行うことにより、結果に影響する因子と処置との間の関係性を取り除くことができるため、見せかけの処置効果は現れず設定通りグループ間に差はないという結果となりました。一方、ランダム化をしなかった場合には、見事に見せかけの処置効果が現れました。

このようにランダム化は処置の効果を正しく推定するための非常に強力な方法なのですが、それでも、偶然によって属性のアンバランスが生じることはありえます。例えば今回の例でも、シミュレーションのうち何回かは性別に無視できないほどの偏りが生じた可能性があります。
特に結果に大きく影響するような属性に関しては、グループ間でバランスが取れるように祈るだけでなく、もっと積極的にバランスを取りにいった方が望ましい場合もあります。そのような方法としては、例えば層別ランダム化が広く利用されています。
次回以降は、そのような方法をまたシミュレーションでやっていこうかと考えています。

今回の記事作成では以下の資料を参考にしました。

[1] 岩崎学(2015), "統計的因果推論", 朝倉書店.
[2] J.L.Fleiss(2004), "臨床試験のデザインと解析", アーム.
[3] gtパッケージについて - TAKAHIRO ONOSHIMA'S WEBSITE
https://onoshima.github.io/stat/gt/

*1:どちらのクーポンも何もしない時と大して結果は変わらない、という可能性は今回は無視することにします。が、このようなケースで一つネタが作れそうなので、今後また出てくるかもしれません。

*2:というよりは、それ以外にシミュレーションをやるための方法が思いつきませんでした。

*3:以降の結果は、p値、信頼区間ともに両側で算出しています。

*4:シミュレーションを通した平均を計算しているので、グループAとBの合計は1にはなっていません。

*5:このような結果になるのは、サンプルサイズが1000とかなり大きいため、些細な差も統計的有意となってしまうからかもしれません。しかしながら、先に述べた単純集計の結果からもこの割り当て方法がまずいことは明らかです。