線形混合モデルにおけるKenward-Roger法：(2)Rによる計算例

R 反復測定データの解析 混合モデル

最終更新：2023/9/10

  • 「実施」セクションの「N=40の欠測なしデータの推定結果」とあるのは「欠測ありデータの推定結果」の間違いでした。修正しました。

はじめに

前回の記事では、線形混合モデルの固定効果に関する推論で使用されるKenward-Roger法の概要を述べていきました。

サンプルサイズが小さい場合、固定効果の分散・共分散を過小に見積もってしまうという問題が知られていたため、補正した推定量を使うことにしようというのがKenward and Roger(1997)の提案でした。
また、固定効果（およびその対比）に関する仮説検定を行う場合に用いる自由度についても、古典的なSatterthwaite法に代わる新たな計算方法が提示されました。

前回は理論的な内容をざっと見るので精一杯でしたので、今回は続編としてRを用いて具体的な計算例を確認していくことにしたいと思います。


今回の流れ

サンプルデータを使用して、Kenward-Roger法がどのような結果を与えるかを実際の数値例で見ていきます。

  1. まずは固定効果の共分散行列について、Kenward-Roger以前の方法（共分散行列を構成するパラメータの推定量を理論的な数式へそのまま代入する）とKenward-Roger法との結果を比較します。
  2. 続いて、自由度の計算結果についてSatterthwaite法とKenward-Roger法それぞれの結果を比較します。

上記の1.と2.を、サンプルサイズが小さい場合（N = 40）と大きい場合（N = 400）、さらに欠測のない場合とある場合とでそれぞれ計算してみます。


サンプルデータと混合モデルの計算に使用するRパッケージ

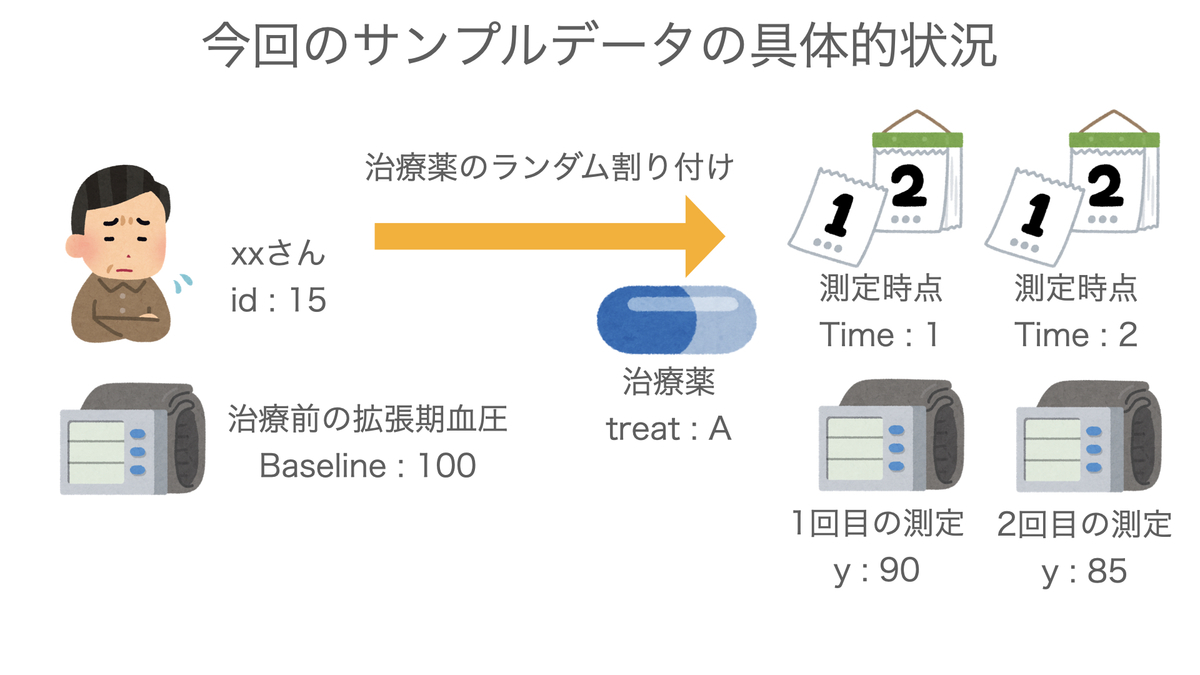
今回は、2つの治療薬の効果を比較するランダム化比較試験を模したサンプルデータを作成してみます。
データ内の変数の説明は以下の通りです。

  • id : 試験に参加した個人を示す番号です。
  • treat : 治療薬の種類です。前半のidにはA薬、後半のidにはB薬が投与されています*1。
  • Baseline : 治療薬の効果として関心のあるアウトカム指標の、治療開始前の値です。例えば血圧などをイメージしていただけるとよいかと思います。
  • Time : 治療開始後の、アウトカム指標を測定した時点です。今回は2回測定しているものとし、それぞれTime1、Time2としています。
  • y : アウトカム指標の値です。混合モデルによって、Time1、Time2の2回の反復測定データをモデリングします。

サンプルサイズが小さいパターン（N = 40。A薬・B薬それぞれに20人）のみ、Rのコード例を示します。

# 使用するパッケージを読み込みます。
library(tidyverse)
library(MASS)

# 乱数のシード値と各群のサンプルサイズを定義します。
set.seed(992)
n1 = 20

# アウトカム測定値の共分散行列を定義します。
# 分散は各時点で同じで、共分散はどの時点間でも同じ(Compound symmetry型)とします。
rho = 0.7      # 異なる時点の測定値間の相関
sigma2 = 5      # 測定値の分散
cov = rho * sigma2      # 測定値間の共分散
covm = diag(sigma2, nrow = 3)      # 共分散行列の対角成分
covm[upper.tri(covm) | lower.tri(covm)] = cov      # 非対角成分に共分散を配置して完成 

# アウトカム測定値の平均ベクトルを定義します。
mu_a = c(100, 90, 80)
mu_b = c(100, 95, 95)

# A薬群、B薬群それぞれのアウトカム測定値を多変量正規分布からサンプリングします。
y1_a = round(mvrnorm(n1, mu = mu_a, Sigma = covm), 1)
y1_b = round(mvrnorm(n1, mu = mu_b, Sigma = covm), 1)
# 縦にならべます。
y1 = rbind(y1_a, y1_b)

# idと治療薬
id1 = rep(1:(n1*2))
treat1 = c(rep("A", n1), rep("B", n1))

# データフレームにまとめて、縦型のデータに変形します。
cd1 = data.frame(id = factor(id1), treat = factor(treat1, levels = c("B", "A")),
                 Baseline = y1[, 1], Time1 = y1[, 2], Time2 = y1[, 3]) %>%
  tidyr::pivot_longer(cols = c(Time1, Time2),
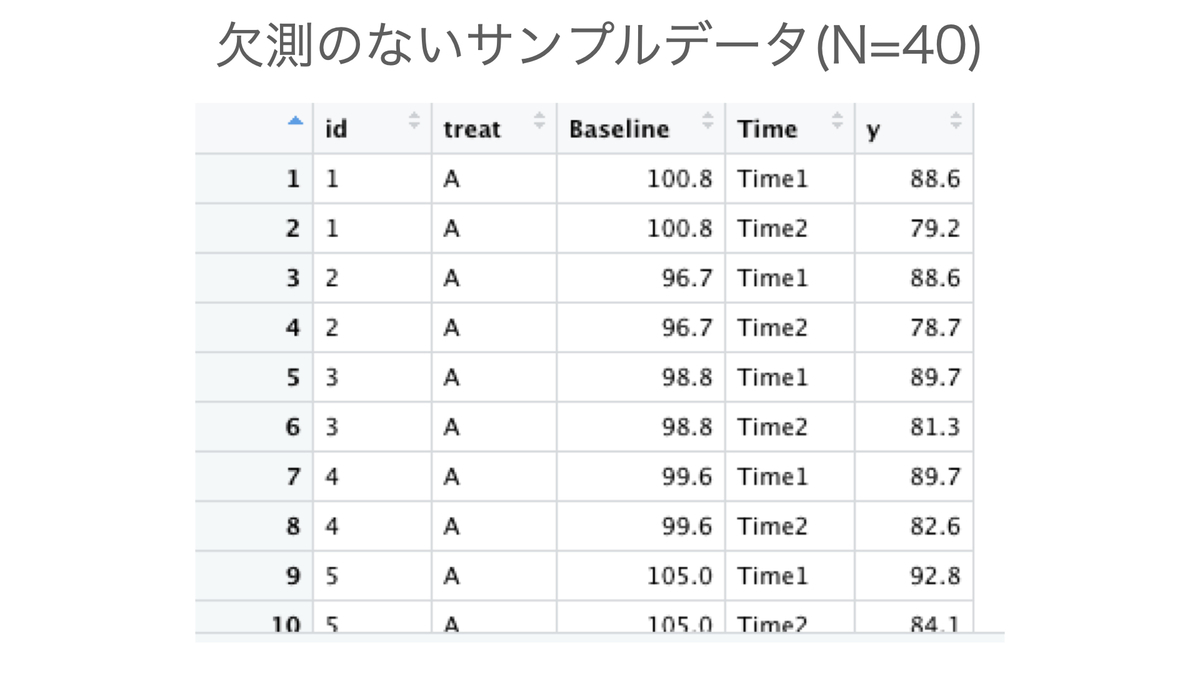
                      names_to = "Time", values_to = "y")

以下のようなデータができます。

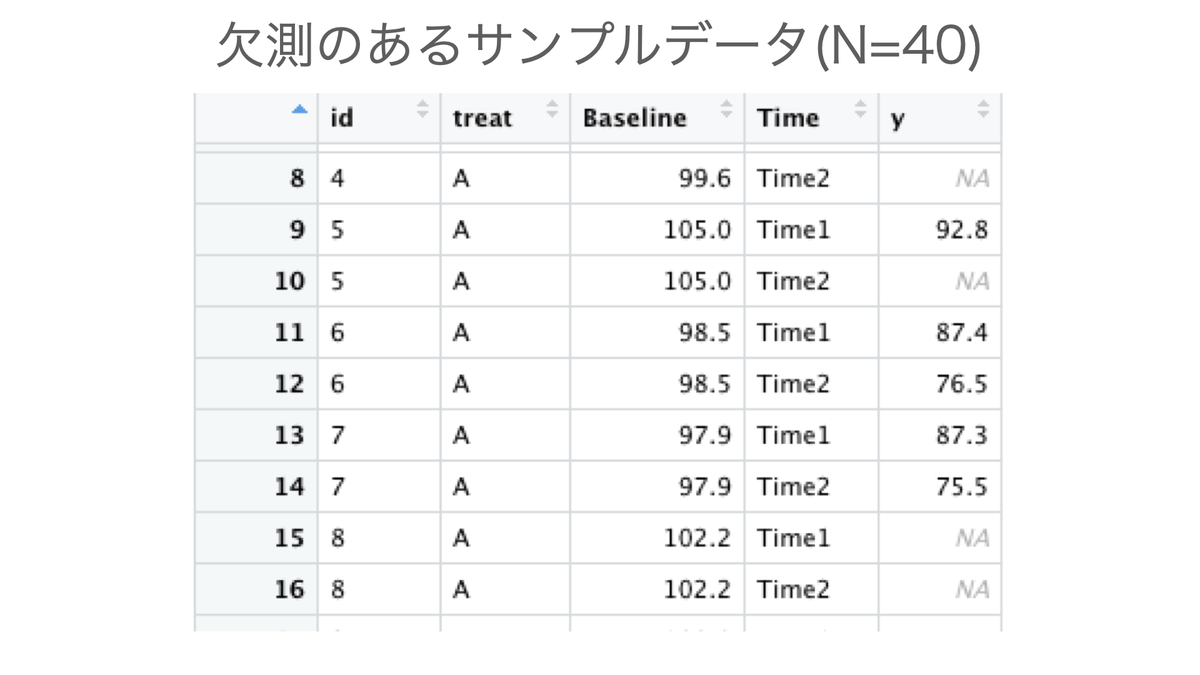
続いて、いくつかのアウトカム測定値が欠測となっているバージョンも作ります。今回は欠測が以前の時点の測定値に依存して起こる、いわゆるMissing at random(MAR)による欠測が一部で生じているような状況を考えます。今回は単純化のため、一度欠測になるとその次の時点も欠測になるようなパターンだけを扱います*2。

データの一部を欠測させるための方法として、今回はmiceパッケージのamputeという関数を使います（参考資料2）。
この関数では、どの変数を欠測させるか、どれくらいの割合で欠測させるか、欠測メカニズムはどのようにするか（MCAR, MAR, MNAR）など細かな指定が可能です。
詳細を書くと本題から外れて長くなってしまうので、次回、amputeを使用した欠測データの作り方の解説を別途していきたいと思います*3。

# miceパッケージを読み込みます。
library(mice)

# 欠測パターンを所定の行列形式で定義します。
# TIme1およびTime2が欠測、Time2のみが欠測という2パターンを定義
patterns = matrix(c(1, 0, 0, 1, 1, 0), nrow = 2, ncol = 3, byrow = TRUE)
rownames(patterns) = c(1, 2)
colnames(patterns) = c("V1", "V2", "V3")

# 各欠測パターンの起こる確率を定義します。
# Time1,2両方欠測する確率は20%, Time2のみ欠測する確率は40%
freq = c(0.2, 0.4)

# 欠測パターンと確率、欠測メカニズムを与えて欠測データを作ります。
y1_amp = ampute(data = y1, freq = freq, patterns = patterns, mech = "MAR")
y1miss = y1_amp$amp

# 完全データと同様にして縦型のデータフレームにまとめます。
md1 = data.frame(id = factor(id1), treat = factor(treat1, levels = c("B", "A")),
                 Baseline = y1miss[, 1], Time1 = y1miss[, 2], Time2 = y1miss[, 3]) %>%
  tidyr::pivot_longer(cols = c(Time1, Time2),
                      names_to = "Time", values_to = "y")

以下のようなデータができました。


混合モデルの計算には、lme4パッケージを使用します。
ただし、今回はKenward-Roger法による分散推定量および自由度の計算を行うための拡張であるlmerTestパッケージを用いました（参考資料4）。
付随して必要となる、pbkrtestパッケージも合わせてインストールしておきました。


実施

各サンプルデータに対して、以下の混合モデルを当てはめます。
ただし i = 1, \cdots, N(N=40 または400)は個人、 j = 1, 2は治療開始後の測定時点を表すインデックスとします。

\displaystyle y_{ij} = \beta_0 + \beta_1 Treat_i + \beta_2 Time_{ij} + \beta_3 Baseline_i + \beta_4 Treat_i \times Time_{ij} + r_i + \varepsilon_{ij}

  • Treatの値は、個人iの受けた治療がAならば1、Bならば0となります。
  • Timeの値は、時点jがTime1ならば0、Time2ならば1となります。
  • Baselineの値は、個人iの治療開始前の測定値です。

また、 r_iは個人iのランダム効果、 \varepsilon_{ij}は個人iの時点jの測定値に関する誤差で、これらは互いに独立に正規分布に従うものとします。

なお本当は前回の記事とのつながりを考えて、誤差の共分散構造を直接指定するタイプのモデル（Covariance pattern modelやMMRM;Mixed model for repeated mearsureと呼ばれるもの）を用いたかったのですが、lme4では実装されていないようであり、Kenward-Roger法を使用できるRのパッケージは他には見つけられませんでした（参考資料4）。
したがって、誤差の共分散構造をCompound symmetryに指定した場合と同じ結果を与えるランダム効果モデル（切片に個人のランダム効果を設定したもの）を使用することにします。

モデル当てはめのRでのコード例は以下の通りです。

# 必要なパッケージを読み込みます。事前にインストールしてください。
library(lmerTest)
library(pbkrtest)

# cd1_lmerという名前で結果を保存します。
# (1 | id)で、切片に個人のランダム効果を設定します。
cd1_lmer = lmer(y ~ treat + Time + Baseline + treat:Time + (1 | id),
                data = cd1, na.action = na.omit)

# パラメータ推定値などは以下で確認できます。
summary(cd1_lmer)

N=40の欠測ありデータの推定結果のみ、以下に例示します。


さて、まずは固定効果の分散・共分散の推定結果について、Kenward-Roger法による調整を行う場合とそうでない場合とを比べてみます。
vcov関数を用いると調整なしの推定結果、vcovAdj関数を用いると調整を行なった推定結果が出力されます。

vcov(cd1_lmer)

# Kenward-Roger法による調整
vcovAdj(cd1_lmer, details = 0)

N=40、N=400で欠測なしのサンプルデータに対して実行した結果は以下のようになりました。


欠測がない場合には、調整をしてもしなくても変わらない結果になりました*4。

一方、欠測がある場合には若干の結果の違いが見られます。


（推定値の違いが比較的大きい部分に色をつけています）
N=40の場合、パラメータによっては0.02〜0.03程度Kenward-Roger法の方が各固定効果の分散（表の対角線上の値）を大きめに推定していることがありますが、それほど大きな差はなさそうです。特に重要な治療効果の分散（treatAとtreatAが交差する箇所）にはほとんど違いがありません。
異なる固定効果どうしの共分散（対角線以外の部分）については、Kenward-Roger法の方が絶対値が大きく推定されているようです。常にそうなるのかはもう少し調査が必要です。


N=400の場合には、両者の違いはほとんどなくなりました。いずれの推定方法でもサンプルサイズが大きくなれば理論的に真の分散に近づくことが数値的に確認できているかと思います。


次に、自由度の計算および固定効果のF検定について見ていきます。
lmerで推定した結果に対してanova関数を適用し、ddfにそれぞれの方法を記載します。

anova(cd1_lmer, ddf = "Satterthwaite")
anova(cd1_lmer, ddf = "Kenward-Roger")




こちらも、欠測がない場合には自由度の計算結果は全く同じになり、F検定も同じ結果になります。
欠測によってデータがアンバランスになる場合に、違いが現れてきます。

まずはN=40の場合を確認します。


どの変数の効果についても、Kenward-Roger法を用いた方が自由度（F統計量の分母にあたる誤差の自由度。DenDFと表記）は小さい数値になり、各効果がゼロでないことを評価するためのF統計量は小さくなります。つまり、統計的有意になりにくくなっています。


一方で、N=400のサンプルデータでは予想に反して、Kenward-Roger法の方が自由度は少し大きめの値になりました。
欠測はN=40の場合と同じように、各グループ平等に同じ割合で起こるように設定しているので、このような結果になるのは欠測状況の違いによるものではなさそうです。
偶然このようなことが起こるのかもしれません。
しかしながら、N=40の場合と比べると各平方和の値は非常に大きいため、自由度の違いがF値に大きく影響はしていないようです。


今回の実験結果をざっとまとめます。

  • 欠測がないデータの場合、Kenward-Roger法を用いた時と用いない時で結果は変わりませんでした。
  • 欠測があるデータの場合、サンプルサイズが小さめ（今回のN=40の場合）であれば、Kenward-Roger法を用いると固定効果の分散・共分散は多少大きめに推定されました。また、F検定の自由度は若干小さく算出されるため、F統計量は小さくなりました。
  • とはいえ、違いは微々たるものでした。サンプルサイズがもっと小さければ、調整効果は大きくなることが予想されます。
  • サンプルサイズが大きくなると（今回のN=400の場合）、結果に違いはほとんどなくなったと言えます。

おわりに

今回のサンプルデータでは、Kenward-Roger法の使用有無による劇的な違いは見られませんでした。N=40では少しサンプルサイズが大きすぎたかもしれません。
どのような場合に大きな違いが生じるのか、もう少し検討してみる必要があるかと思います。

また、今回は治療グループ間に差があるという状況のサンプルデータを作成したため、Type1 errorが名目の有意水準（例えば両側5%）を超えてしまうかどうかという問題は検討していません。原論文（参考資料1）でも述べられている重要な点であるので、次回以降にこの検討もおこなってみます。

次回は、本題から外れるため詳しくは触れなかった、miceパッケージを用いた欠測データの作成方法を考えていきたいと思います。

今回は以下の資料を参考にしました。
[1] Kenward, M., & Roger, J. (1997). Small Sample Inference for Fixed Effects from Restricted Maximum Likelihood. Biometrics, 53(3), 983-997.
[2] Generate missing values with ampute.
https://www.gerkovink.com/Amputation_with_Ampute/Vignette/ampute.html
[3] Mixed model repeated measures (MMRM) in Stata, SAS and R, The Stats Geek.
https://thestatsgeek.com/2020/12/30/mixed-model-repeated-measures-mmrm-in-stata-sas-and-r/
[4] Kuznetsova, A., Brockhoff, P., & Christensen, R. (2017). lmerTest Package: Tests in Linear Mixed Effects Models. Journal of Statistical Software, 82(13), 1 - 26.
https://www.jstatsoft.org/article/view/v082i13
[5] Bates, D., Mächler, M., Bolker, B., & Walker, S. (2015). Fitting Linear Mixed-Effects Models Using lme4. Journal of Statistical Software, 67(1), 1 - 48.
https://www.jstatsoft.org/article/view/v067i01

*1:ランダム化をするとidはランダムに振られるはずなので現実にはこのような番号づけにはなりませんが、単純化のためこのようなデータの作り方にしています。

*2:例として、薬を飲んでも効果がないように感じられて、途中で臨床試験への参加をやめてしまうような場合などがあります。

*3:実は今回1つごまかしがあって、miceパッケージで実行できる多重代入法の1つMICE法の性質を考えると、Time1で欠測になるかどうかがTime2の情報にも依存するような設定になっているのではないかと思います。経時的にデータをとった場合そのようなことは考えにくいですが、今回はサンプルデータの作り方にこれ以上は触れず、データの一部に欠測があることが混合モデルの計算結果にどう影響するかという点だけを考えることにします。

*4:一部、例えば最後にe-15とかがついている箇所は数値が違いますが、計算方法の違いによるものと思われ、実質的には0です。