2021-04-02

シミュレーションで理解するランダム化比較試験：(1)ランダム化の効果を確認する

R 実験計画法

はじめに

異なる処置の間に効果の違いがあるかどうかを評価するための方法として、「ランダム化(Randomization)」と呼ばれる方法が広く知られています。ランダム化は、処置の効果を歪める*1さまざまな要因の影響を取り除くことができ、処置と結果との因果関係を実証するための最も有効な方法とされています。

例えば新治療の効果が標準治療を上回るかどうかを確かめたい場合には、患者さんを新治療を受けるグループと標準治療を受けるグループにランダムに分け、患者さんの属性（年齢、性別、重症度など・・・）が両グループ間でバランスが取れるようにします*2。例えば重症の患者さんばかりが標準治療を受け、軽症の方ばかりが新治療を受けてしまうと、新治療のほうが良好な結果が得られてしまう可能性があります。このように、属性の違いが結果に影響することを防ぐことが目的です。

また別の例として、Webページに表示する広告をランダムに出し分けることで、広告AとBとの間でサイト閲覧や商品購入に至る割合に違いがあるかを検討するなどの応用も知られています*3。

さて、ではランダム化を行うと、本当にグループ間で属性のバランスが取れるのでしょうか？
今回は、Rを使ってシミュレーションしてみることにします。

問題設定

こんな事例を考えて見たいと思います。
とあるアパレルショップでは、新規にアプリ会員登録をしたお客さんを対象に、次回の来店時に使用できるクーポンを配布することにしました。ただし、クーポンの内容をどうするかについては社内で議論があり、以下の2つのどちらが次回の購入金額アップにつながるかを確かめたいということになりました。

(クーポンA)：5,000円以上の買い物をした場合に1,000円を割引
(クーポンB)：10,000円以上の買い物をした場合に購入金額の10%を割引

さらに、一度の購入単価はお客さんの属性（年齢、性別、収入、など・・・）によってかなり違いそうだという意見が出たため、どちらのクーポンを配布するかをランダムに決めることでクーポンA/Bそれぞれの配布されるお客さんの属性が偏らないよう配慮し、平均的にどちらのクーポンを配布したグループの売り上げが高くなるかを評価しよう、と会議で決定しました。

f:id:mstour:20210402212611j:plain

さて、どちらのクーポンを配布するかは会員登録時点でランダムに決まるものとした場合、クーポンAを渡されたグループとクーポンBを渡されたグループの属性は似たようなものになるでしょうか？

話を簡単にするため、今回は以下の3つの属性に注目することにします。
(1) 性別（男性、女性）
(2) 年齢カテゴリー（20代以下、30代、40代以上）
(3) 会員登録時の購入金額（単位：円）

今回はクーポンAグループとクーポンBグループの平均的な購入金額を比較することになるので、(3)は評価したい結果そのものの処置前*4の値となります*5。
血圧のように測定の度に変化しやすいような数値をイメージするとわかりやすいのですが、たまたま高い値が出たとしても、次回測定した時にはそこまで高い値にはならず、何度も測定を繰り返すとその人の本来の値に落ち着くということが往々にしてあります*6。このような現象は「平均への回帰(Regression to the mean)」と呼ばれます。

今回の例では、会員登録時点ではあまり大きな買い物をしなかった場合、次回来店時には比較的購入金額が大きくなる可能性があります（逆に、前回大量の買い物をした場合には、次回は購入金額がそれほど大きくならないことが予想されます）。そうすると仮に登録時点の購入金額が少ない人ばかりにクーポンAが配布された場合、本当はクーポンAとBとで効果に違いがなかったとしても、クーポンAはクーポンBよりも次回の購入金額が大きくなってしまうかもしれません。
平均への回帰を処置の効果と混同しないよう、ランダム化によって比較するグループの間で処置前の値が偏らないようにすることが重要です。

少し話が脇道にそれてしまいました。続いて、今回のシミュレーションの説明に移ります。

シミュレーション方法

クーポンA、クーポンBをそれぞれ500人ずつに配布するという企画を実施するものとします。

まずは、新規会員登録したユーザーの仮想的なデータを作ってみましょう。
以下のように、ユーザーの属性データを作成します。

library(tidyverse)
library(TruncatedNormal)

n_half = 500
set.seed(1234)

# 乱数発生
gender = c(rbinom(n_half, 1, 0.7), rbinom(n_half, 1, 0.3))
agecat = rbind(t(rmultinom(n_half, 1, c(0.6, 0.3, 0.1))),
               t(rmultinom(n_half, 1, c(0.1, 0.3, 0.6))))
buy_bl = c(round(rtnorm(n = n_half, mu = 20000, sd = 5000, lb = 3000, ub = 50000)),
           round(rtnorm(n = n_half, mu = 10000, sd = 5000, lb = 3000, ub = 50000)))

users_0 = data.frame(GENDER = gender,
                   AGE20 = agecat[, 1],
                   AGE30 = agecat[, 2],
                   AGE40 = agecat[, 3],
                   BUY_BL = buy_bl)
# 文字型の変数も作る
users = mutate(users_0,
               GENDERC = factor(case_when(
                 GENDER == 1 ~ "F",
                 GENDER == 0 ~ "M"
               )),
               AGEC = factor(case_when(
                 AGE20 == 1 ~ "20s or younger",
                 AGE30 == 1 ~ "30s",
                 AGE40 == 1 ~ "40s or older"
               )))

2カテゴリーの変数である「性別」は二項分布からのサンプリング（rbinom関数）、3カテゴリーの「年齢カテゴリー」は多項分布（rmultinom関数）を利用して作成しています。
また、連続値である「会員登録時の購入金額」は切断正規分布(Truncated normal distribution)*7から生成しました。洋服の一度の購入金額ということなので、ここでは値が3,000円から50,000円の範囲になるように設定しています。切断正規分布からのサンプリングにはTruncatedNormalパッケージのrtnorm関数を使用しました。
ここで、前半の500サンプルは女性が出やすく、後半は逆に男性が出やすく設定しているのがポイントです。その他の属性も同様に設定しています。

次に、クーポンA・Bの割り当て方法を2通り用意します。
1つめの方法では、ランダム化をせず、単純に前半の500人にはクーポンAを、後半の500人にはクーポンBを渡すことにします。

# 割り当て方法1：ランダム化ではない
alloc1 = c(rep("A", n_half), rep("B", n_half))

2つめの方法では、クーポンAとクーポンBのどちらを配布するかをランダムに決定します（ランダム化です）。これは、単純にAとBがランダムに並ぶベクトルを作ればよいので、先に作成したalloc1をランダムに並べ替えます。

# 割り当て方法2：ランダム化
alloc2 = sample(alloc1)

最後にこの両方をユーザー属性のデータセットに結合しましょう（性別、年齢カテゴリーは、文字型のみ残しました）。

users_alloc = mutate(users[, 5:7], ALLOC1 = factor(alloc1), ALLOC2 = factor(alloc2))

では、クーポンの割り当て方法1（ランダム化なし）と2（ランダム化）のそれぞれで、ユーザーの属性がどのようになったかを確認してみましょう。

ランダム化の結果

属性の集計には、gtsummaryパッケージを使用してみます。

library(gtsummary)

割り当て方法1（ランダム化なし）を行った場合の、クーポンAを配布されたグループとBを配布されたグループそれぞれのユーザー属性を集計してみましょう。
なお、ここではgtsummaryの詳細は割愛します。記法については以下のサイトが参考になります。
note.com
qiita.com

tbl_summary(users_alloc[, -5], by = ALLOC1,
            statistic = list(BUY_BL ~ "{mean}({sd})"),
            digits = list(BUY_BL ~ 1),
            label = list(BUY_BL ~ "Previous sell(Yen)",
                         GENDERC ~ "Gender",
                         AGEC ~ "Age category")
)

結果は以下の通り、クーポンAは女性や若い人に多く配布され、クーポンBは男性や高年齢の人に多く配布されてしまっています。また前回の購入金額の平均にも大きな開きがあります。

f:id:mstour:20210402200153p:plain
もし男性の方が購入金額が高かったり、年齢が高いほど購入金額が高かったりする傾向にある場合、仮にクーポンBのグループの平均的な売り上げがクーポンAより高かったとしても、その効果は本当にクーポンBによるものなのかはっきりしません。この企画ではきっとうまくいかないでしょう。

では、どちらのクーポンを配布するかをランダムに決める割り当て方法2ではどうでしょうか？

tbl_summary(users_alloc[, -4], by = ALLOC2,
            statistic = list(BUY_BL ~ "{mean}({sd})"),
            digits = list(BUY_BL ~ 1),
            label = list(BUY_BL ~ "Previous sell(Yen)",
                         GENDERC ~ "Gender",
                         AGEC ~ "Age category")
)

結果は以下のようになりました。

f:id:mstour:20210402200401p:plain
割り当て方法1に比べて、どの属性も2グループ間でバランスが取れていることがわかります。
したがって公平な比較が可能になり、グループ間の売り上げの違いはクーポンの効果によるものであると考えることができます。

さらに重要なのは、ランダム化を行うことにより、ここでは見ていないその他のあらゆる属性についてもバランスが取れるという点です。
頑張ればデータを集められるような属性であれば、それらの影響を分析の際に調整することも可能ですが*8、データを集められないような属性についてもランダム化によって均等になることが期待できます。

まとめ

今回は、異なる処置を対象者へランダムに割り当てること（ランダム化）により、対象者の属性が処置のグループ間でバランスが取れることを簡単なシミュレーションでみていきました。
上記のような単純なランダム化で十分なこともありますが、場合によってはさらに込み入った方法を用いなければならないこともあります。
次回はもう少し難しい例題を使って考えてみたいと思います。

今回の記事作成では以下の資料を参考にしました。

[1] 岩崎学(2015), "統計的因果推論", 朝倉書店.
[2] 大城信晃他(2020), "AI・データ分析プロジェクトのすべて", 技術評論社.
[3] J.L.Fleiss(2004), "臨床試験のデザインと解析", アーム.
[4] 「gtsummary」を使って論文に載せる表を作成してみた
https://note.com/exerciseandbrain/n/n755df620d42a
[5] 【R】データ要約ガチ勢のためのgtsummaryで表を書こう
https://qiita.com/yanami/items/117851de49024f5980d0

*1:本当は効果がないのに数値上に見せかけの効果が現れてしまう場合もありますし、逆に本当は効果があるのにその効果が隠されてしまうような場合もあります。

*2:医学分野では、このような研究を「ランダム化比較試験(Randomized controlled trial; RCT)」と呼びます。

*3:Webの分野では「A/Bテスト」という呼ばれ方が多いようです。

*4:ここでの「処置」とは、クーポンAまたはBを配布することです。

*5:医学分野では「ベースライン」と呼ぶことが多くあります。

*6:ここでは健康な人を念頭において考えています。

*7:とりうる値の範囲を制限した正規分布のことです。

*8:例えば線形モデルの説明変数に含めることによって、それらの属性の影響を取り除いた評価を行うことができます。しかしながら、データを取ることが困難であったり、そもそも観察すらできないような何かの影響についてはモデルによる分析では対処のしようがありません。

2021-03-23

反復測定データのモデリング：(5)一般化線形混合モデル

反復測定データの解析一般化線形モデル最尤法カテゴリカルデータ

はじめに

前回は、正規分布に従うと想定できないような反復測定データの分析を行うための有力な方法である一般化推定方程式(GEE)を紹介しました。この方法は一般化線形モデル(GLM)と同様のモデリングを行うのですが、目的変数に特定の確率分布を想定せずにパラメータの推定を行うのが特徴です。

今回は、正規分布を仮定せずに分析を行うもう一つの代表的な方法である、一般化線形混合モデル(Generalized linear mixed model; GLMM)について見ていこうと思います。
GLMMはGLMと混合モデルとを組み合わせたモデルであり、GLMを直接拡張したモデルであると言えます。

f:id:mstour:20210323212456j:plain

GLMMもGEEと同じく、整数値のデータ、二値のデータなど、さまざまなデータに対して適用することができます。まずは典型的な使用例を紹介し、続いて一般的な定義を確認していきたいと思います。

GLMMの例

GEEについて紹介した前回の記事でも説明に用いた、てんかんの発作回数に関する反復測定データを分析することを考えてみましょう*1。
この例では、新治療か既存治療かのいずれかを受けた各個人について、複数の期間に分けててんかんの発作回数を記録し、発作の発現率（週あたりの発作回数）について新治療と既存治療とでどの程度の差があるかを評価することが分析の目的です*2。
mstour.hatenablog.com

個人 $i$ の $j$ 回目の観察期における発作回数を $y_{ij}$ とし、これらはそれぞれパラメータ $\mu_{ij}$ のPoisson分布に従うと想定します。Poisson分布に従う確率変数の期待値はパラメータと等しいので、個人 $i$ の期間 $j$ での発作回数の平均（観測された値の単純な平均ではなく、目には見えないが存在するであろうと想定する「真の値」）が $\mu_{ij}$ であると考えていることになります。
また、 $x_i$ を個人 $i$ が受けた治療を示す変数（新治療の場合1、既存治療の場合0）、 $t_{ij}$ を個人 $i$ の観察期 $j$ の長さ（単位は週とします）とします。
このとき、GEEでは、GLMと同様の以下のようなモデル

$\displaystyle \log \mu_{ij} = \beta_0 + \beta_1 x_i + \log t_{ij}$

を考え、モデルのパラメータを推定する際に目的変数 $y_{ij}$ の間に相関があることを考慮することになっていました。

一方で、GLMMでは目的変数どうしに相関があることをモデル式そのものに反映させます。これは、以前に紹介した（正規分布の場合の）混合モデルと全く同じ考え方です。
mstour.hatenablog.com

つまり、同じ個人の測定値どうしは個人差の影響によってある程度似通ったものになると考えるのが自然であるため、個人差を表すランダム効果をモデル式に含めます。
個人差は説明変数と同じく観測値（目的変数）へ影響を与えるものと考え、例えば

$\displaystyle \log \mu_{ij} = \beta_0 + \beta_1 x_i + r_i + \log t_{ij}$

のようなモデルを想定します。 $r_i$ が個人 $i$ に由来する特徴、つまり個人差を表すランダム効果です。
上記のモデルは、個人 $i$ の各観察期 $j = 1, \cdots, T$ それぞれにおける発作回数の真の値 $\mu_{i1}, \cdots, \mu_{iT}$ に共通する部分 $r_i$ があることを想定しており、観測された値 $y_{i1}, \cdots, y_{iT}$ どうしが似ていることを直接表現しています。

f:id:mstour:20210323212512j:plain

見方を変えると、通常のGLMでは説明変数 $x_i$ による影響以外は誤差的なばらつきとして扱われる一方、ランダム効果 $r_i$ を導入することによって、誤差的なばらつきから個人差による影響を分離することができるため、より精度の高い推定が可能になると言えます（この点は、通常の混合モデルでも全く同様です）。

GEEと異なり、目的変数の確率分布としてPoisson分布を明示的に仮定しているため、関心のあるパラメータ $\beta_1$ は最尤法に基づいて推定することができます。

一般的な定義

続いて、GLMMの一般的な定義を見ていきたいと思います。ここでも反復測定データを念頭に置いた説明をすることにしますが、データどうしに相関の生じるその他の場面、例えば同じ地域に住む人どうしの相関を考慮しなければならないようなときでも基本的な考え方は同じです。
表記は前回の記事で紹介したGEEと同様のものを使用することにします。すなわち、目的変数である反復測定データベクトルを $\boldsymbol{y}_i (i = 1, \cdots, N)$ 、それらが従う確率分布の平均パラメータを $E(\boldsymbol{y}_i) = \boldsymbol{\mu}_i$ とします。

通常のGLM（およびGEE）の場合、平均パラメータと説明変数との関係を以下のモデル式

$\displaystyle g(\boldsymbol{\mu}_i) = X_i^T \boldsymbol{\beta}$

で表現しました。ここで行列 $X_i^T$ は、各時点の反復測定データに対応する説明変数ベクトル $\boldsymbol{x}_{ij}^T$ を縦に並べたもの*3です。

GLMMは、このモデルにランダム効果を加えた

$\displaystyle g(\boldsymbol{\mu}_i) = X_i^T \boldsymbol{\beta} + Z_i^T \boldsymbol{u}$

という形のモデル式で表現されます。
$\boldsymbol{u}$ はモデルに含まれる全てのランダム効果からなるベクトルで、 $Z_i$ は「ランダム効果が設定される説明変数」のベクトルを縦に並べたもの*4です。
混合モデルに関する以前の記事でも触れましたが、モデルの切片の部分にランダム効果を設定する*5だけではなく、説明変数の効果に関してもランダム効果を付加することができます*6。 $Z_i$ にはランダム効果が設定された説明変数と、切片に対応する「1」が含まれることになります。

ランダム効果が何らかの確率分布に従うとする点も、正規分布の場合の混合モデルと同様です。ランダム効果（からなるベクトル $\boldsymbol{u}$ ）は（多変量）正規分布に従うものと設定することが一般的です。

このように、GLMMには、目的変数が正規分布の場合の混合モデルと共通する部分が多くありますが、パラメータ（モデル右辺の固定効果 $\boldsymbol{\beta}$ と、ランダム効果・誤差それぞれの分散）の推定において少し異なる部分があります。
正規分布の混合モデルの場合には、例えば固定効果の推定結果*7は

$\displaystyle \hat{\boldsymbol{\beta}} = (X^T V^{-1} X)^{-1} X^T V^{-1} \boldsymbol{y}$

のように書き下すことができましたが、GLMMの推定にはさまざまな難点があることが知られています。
そのためGLMMでは、尤度関数を近似することで推定計算を行う方法がいくつか提案されています。

まとめと参考資料

一般化線形混合モデル(GLMM)は、正規分布を想定するのに無理があるような反復測定データの分析に有効な方法の一つです。
前回紹介したGEEと基本的には同様の方法と言えますが、GLMMの説明変数の効果（固定効果）は「同じ人（同じランダム効果を持つ人）が、もし説明変数の値が違っていた場合にどの程度の影響があるか」を示しており*8、このような条件をおかないGEE*9とは多少意味合いが異なるところがあります*10。

少し理論的な内容が続いたため、本シリーズはいったんここで区切り、次回は別の話題を考えたいと思います。

本記事の作成にあたっては以下の資料を参考にしました。
[1] SAS/STAT User's Guide, The GENMOD Procedure.
https://documentation.sas.com/?cdcId=pgmsascdc&cdcVersion=9.4_3.4&docsetId=statug&docsetTarget=statug_genmod_examples07.htm&locale=en
[2] SAS/STAT User's Guide, The GLIMMIX Procedure.
https://documentation.sas.com/?cdcId=pgmsascdc&cdcVersion=9.4_3.3&docsetId=statug&docsetTarget=statug_glimmix_details07.htm&locale=en
[3] RANDOM COEFFICIENT POISSON MODELS | R FAQ, UCLA Statistical Consulting.
https://stats.idre.ucla.edu/r/faq/random-coefficient-poisson-models/
[4] Brown and Prescott(2015), "Applied Mixed Models in Medicine", Wiley.
[5] Gory et al. (2020), "A class of generalized linear mixed models adjusted for marginal interpretability", Statistics in Medicine. 2020;1–14.

*1:データの詳細は、参考資料[1]をご参照ください。

*2:前回も述べた通り、Poisson分布を用いた回帰では、新治療を受けたグループの発現率が既存治療を受けたグループの何倍になるか（率比(Rate ratio)）により結果を要約することが行われます。例えば率比が0.5であれば、新治療は既存治療よりも発作の発現を半減させるという解釈になります。

*3:すなわち、固定効果に関するデザイン行列です。

*4:ランダム効果に関するデザイン行列です。

*5:目的変数の値の平均的な水準に個人差があることを考えていることになります。

*6:介入の効果、時間による変化、リスク因子の影響など、説明変数が目的変数へ与える影響の大きさに個人差があることを表現しています。

*7:正確には、値が確率的に変動する「推定量」のことを指しています。得られたデータから計算される値である「推定値」とは厳密には異なります。

*8:このようなモデルは「条件付きモデル(Conditional model)」や「Subject-specific model」と呼ばれます。

*9:GEEは、個人の効果を考慮せず集団全体での説明変数の効果を考えます。こちらは「周辺モデル(Marginal model)」や「Population-average model」と呼ばれます。

*10:実務上でそこまで厳格に使い分けられているかは、よく分かりません。ただし、GLMMとGEEとでは一般に推定結果は異なります。なお正規分布の場合には、条件付きモデルである混合モデルと、周辺モデルであるCovariance pattern modelとの結果は一致するため、厳格な使い分けが議論になることはあまりないのではないかと思います。

2021-03-12

反復測定データのモデリング：(4)一般化推定方程式

反復測定データの解析一般化線形モデルカテゴリカルデータ最尤法

はじめに

当ブログではこれまで反復測定データの解析方法のいくつかを紹介してきたが、今のところ目的変数の確率分布に正規分布を想定するものにとどまっていた。
当然、現実の場面ではそうではないデータに対峙することも多く、例えば二値や整数値で記録される反復測定データを扱わなければならない場合もある。

今回は、正規分布以外の反復測定データを解析するための方法として知られている「一般化推定方程式(Generalized estimating equation; GEE)」について考えてみたい。以下、広く用いられている略称であるGEEという表現で統一する。
この方法は、通常の線形モデルとは異なりデータの背後にある確率分布を明示的に特定しないのが大きな特徴である。したがって、正規分布からかけ離れた分布構造を持つデータにも適用可能となるのだが、確率分布を使わないことによるデメリットも存在する。

まずは、GEEの概要を見ていこう。

概要（具体例を交えて）

目的変数が反復測定データではなく1個人につき1個の場合、正規分布以外の確率分布を想定したモデリングを行うには一般化線形モデルを用いることが多い。
例えば、新しい治療が既存治療よりも「てんかん発作」の1週間あたりの発現回数（回/週）を抑えられるかどうかを検討したいという場合、治療開始後の観察期間における発現回数がPoisson分布に従うと想定した一般化線形モデル（Poisson回帰と呼ぶことが多い）を用いることで、発作の発現率（単位時間あたりの発現回数。ここでの例では、週あたりの発現回数を評価したいと考えている）に治療が与える影響を評価することができる。

f:id:mstour:20210312205441j:plain

治療開始から一定の期間にわたって発作発現回数を記録したものとし、その期間の個人 $i$ の発現回数を $y_i$ とする。Poisson回帰によって解析する場合、 $y_i$ はそれぞれパラメータ $\mu_i$ を持つPoisson分布に従うと想定し、 $\mu_i$ について次のようなモデル

$\displaystyle \log \mu_i = \beta_0 + \beta_1 x_i + \log t_i$

が考えられる。

f:id:mstour:20210312205510j:plain

ここで $x_i$ は治療を表す変数で、新治療を受けた場合1、既存治療を受けた場合0をとる*1。また $t_i$ は個人 $i$ の発作の観察期間（週）とする*2。

このモデルにて推定された $\beta_1$ の値の指数をとると、新治療を行った時の「週あたりの発現回数」が既存治療の何倍になるかが算出できる*3。

さらに、それぞれの個人のてんかん発作の回数が1つの期間だけではなく、複数の期間に分けて記録されており（つまり、反復測定データになっている）、それらの情報を全て用いて週あたりの発作発現回数を評価したいものとしよう*4。
この場合、同じ個人から得られたデータどうしには相関が生じるため、全てのデータを独立とみなしたPoisson回帰モデルをそのまま当てはめるのは適切ではないだろう*5。そこで、一般化線形モデルの理論を踏まえつつ互いに相関のあるデータをモデリングできる方法であるGEEが有用となる。

f:id:mstour:20210312205536j:plain

GEEにおいては、基本的なモデル式は一般化線形モデルと同様のものが用いられる。Poisson回帰を行うここでの事例では、個人 $i$ の $j$ 回目の測定データ（ $j$ 回目の観察期間における発作回数） $y_{ij}$ がパラメータ $\mu_{ij}$ を持つPoisson分布に従うと想定し*6、例えば一般化線形モデルの場合と同様に

$\displaystyle \log \mu_{ij} = \beta_0 + \beta_1 x_i + \log t_{ij}$

というモデルを考える。
しかしながら、既存治療に対する新治療の効果（週あたり発作回数が何倍になるか）などの未知パラメータの推定は、目的変数に相関があることを考慮した上で行われる。

モデル式のパラメータ（上記の例では $\beta_0, \beta_1$ ）をGEEによって推定した結果は、一般化線形モデルの最尤法による推定と同様に真の値に対して一致性を持つ*7。また推定値の分布はサンプルサイズが大きくなるにつれて正規分布に近づくので、このことを利用して関心あるパラメータ（例えば、既存治療に対する新治療の効果を示す $\beta_1$ ）についての信頼区間を計算することなどができる。

当然、Poisson分布だけでなくその他の分布が適切と考えられるような場合でもGEEを用いることができる。またSAS、R、SPSSなど広く利用されている統計ソフトにはたいてい実装されているようであり、汎用性の高い方法と言えるだろう。

一方で、GEEは最尤法による推定を行わないため、混合モデルとは異なり欠測メカニズムがMARの場合に推定結果が真の値に近づく（一致推定量になる）ことは保証されていないという難点がある。
欠測メカニズムがMARである場合にも妥当な方法として、一つは一般化線形モデルにランダム効果を導入する「一般化線形混合モデル(Generalized linear mixed model; GLMM)」がある。GLMMは最尤法による推定を行うので、MARの場合にも真の値に近づくような推定結果を得ることができる。
他には、GEEを直接拡張する方法として、観測確率の推定値の逆数で重みづけを行う「IPW推定方程式」と呼ばれる方法を用いることでMARの場合にも妥当な推測ができることが知られている。

数学的詳細

GEEの考え方自体はシンプルで、正規分布の想定が適切とは限らない場合に、互いに相関のあるデータも全て利用することでより精度の高い推定を行うための方法であると理解できる。
しかしながら、数学的な詳細は（少なくとも筆者には）直感的になかなか理解しにくい部分がある。理論的な側面を少しだけ追ってみよう。

まずは通常の一般化線形モデルから話を進める。
関心のある目的変数を $y_i (i = 1, \cdots, N)$ 、その期待値を $E(y_i) = \mu_i$ とする。先のPoisson回帰の例では $\mu_i$ は $y_i$ が従うと想定するPoisson分布のパラメータである。
これに対して、説明変数ベクトル $\boldsymbol{x}_i$ （切片に対応する1を要素に含む）を用いた一般化線形モデル

$\displaystyle g(\mu_i) = \boldsymbol{x}_i^T \boldsymbol{\beta}$

を当てはめる状況を考えよう。ここで $\boldsymbol{\beta} = (\beta_0, \beta_1, \cdots, \beta_P)^T$ は未知のモデルパラメータとする。一般化線形モデルについては以前の記事もよければご覧いただきたい。

パラメータの推定を行うには、想定する確率分布から作られる「尤度(Likelihood)」を最大化するようなパラメータの値を求める必要がある。実際には、尤度の対数をとった「対数尤度(Log likelihood)」が最大になるようなパラメータの値を計算する。
対数尤度を $\ell$ とすると、パラメータ $\beta_p$ の推定値は $\ell$ を $\beta_p$ で偏微分した結果を0と等しいとした方程式を解くことで得られる：

$\displaystyle \frac{\partial \ell}{\partial \beta_p} = 0$

左辺は $\beta_p$ についての「スコア統計量(Score statistics)」といい、以降では $U_p$ と表す。またスコア統計量が0に等しいとおいた方程式は「スコア方程式(Score equation)」と呼ばれ、以下のように表されることが知られている。

$\displaystyle U_p = \sum_{i=1}^{N} \frac{(y_i - \mu_i)}{Var(y_i)} \frac{\partial \mu_i}{\partial \beta_p} = 0 \hspace{10pt} (p = 0, 1, \cdots, P)$

全てのパラメータに関するスコア統計量を縦に並べたものを $U$ とすると、次のように表せる。

$\displaystyle U = \sum_{i=1}^{N} \frac{(y_i - \mu_i)}{Var(y_i)} \frac{\partial \mu_i}{\partial \boldsymbol{\beta}} = \boldsymbol{0} \hspace{30pt} (1)$

この方程式を $\boldsymbol{\beta}$ について解いた結果がパラメータの真値の一致推定量になることは最尤法の理論から導かれるが、実は目的変数の従う確率分布を具体的に特定しなくても、ある条件を満たせば同様の結果が得られることが示されている。
確率分布を特定しない場合に、上記のスコア方程式は「擬似尤度推定方程式(Quasi-likelihood estimating equation)」と呼ばれている*8。

これをさらに一般化して、確率分布を特定せず、さらに互いに相関のあるデータの場合にも拡張したものがGEEである。
GEEを用いる場面を想定して、今度は目的変数を反復測定データのベクトル $\boldsymbol{y}_i (i = 1, \cdots, N)$ とする。目的変数は、平均ベクトル $E(\boldsymbol{y}_i) = \boldsymbol{\mu}_i$ 、共分散行列 $V_i$ となるような何らかの（多変量）確率分布に従うものとする*9。また、平均に関して一般化線形モデル

$\displaystyle g(\boldsymbol{\mu}_i) = X_i^T \boldsymbol{\beta}$

によるモデリングを考える（行列 $X_i^T$ は、各時点の反復測定データに対応する説明変数ベクトル $\boldsymbol{x}_{ij}^T$ を縦に並べたもの）。

GEEによるパラメータ推定は、式(1)を多変量に拡張した

$\displaystyle U = \sum_{i=1}^{N} \left( \frac{\partial \boldsymbol{\mu}_i}{\partial \boldsymbol{\beta}} \right) V_i^{-1} (\boldsymbol{y}_i - \boldsymbol{\mu}_i) = \boldsymbol{0} \hspace{30pt} (2)$

をパラメータベクトル $\boldsymbol{\beta}$ について解くことで行う*10。
もっとも、実際に解くためには反復計算が必要となる。

データ間に相関があることを考慮するために、式(2)の $V_i$ に、想定されるデータ間の相関の構造を直接指定することができる。やり方は以前に紹介したCovariance pattern modelと同様である。

GEEによるパラメータの推定結果は一致性を持つことが知られているが、例えば分散の推定方法など他にも考えないといけない点がある。長くなってきたので、今度また応用編的な内容として続きを書いていきたい。

まとめ

今回は、正規分布ではモデリングできないような反復測定データにも使用できる方法である一般化推定方程式(GEE)をざっと紹介した。
多くの統計ソフトで実行可能であり、特に整数値をとるカウントデータや二値データの解析に広く活用されているようである。詳しい話はまだ書ききれていないので、また次回へ続くということで・・・

参考文献
[1] SAS/STAT User's Guide, The GENMOD Procedure.
https://documentation.sas.com/?cdcId=pgmsascdc&cdcVersion=9.4_3.4&docsetId=statug&docsetTarget=statug_genmod_examples07.htm&locale=en
[2] Yang et al.(2020), "Transcranial direct current stimulation reduces seizure frequency in patients with refractory focal epilepsy: A randomized, double-blind, sham-controlled, and three-arm parallel multicenter study", Brain Stimul. Jan-Feb 2020;13(1):109-116.
https://www.brainstimjrnl.com/article/S1935-861X(19)30369-9/fulltext
[3] Annette J. Dobson(2008), "一般化線形モデル入門", 共立出版.
[4] John M. Lachin(2020), "医薬データのための統計解析", 共立出版.
[5] 高井啓二・星野崇宏・野間久史(2016), "欠測データの統計科学", 岩波書店.

*1:交絡因子などを含めると話が複雑になるので、治療はランダムに割り付けられているものとする。

*2: $\log t_i$ はオフセット項と呼ばれる。例えば観察期間が長い個人ほど発作の発現回数は多くなる可能性が高いので、全員の観察期間を揃えて評価するために使用される。少し古い記事だがこちらでも紹介した。

*3:この指標は、率(Rate)の比をとったものなので「率比(Rate ratio)」と呼ばれることがある。

*4:ここでの例は文献[1]に記載の古典的な例を参考にしたが、例えば文献[2]など最近でも同様の事例が見つけられる。

*5:文献[1]では推定結果のばらつき（標準誤差）を小さく見積もってしまう例が紹介されているが、文献[3]では逆にばらつきを大きく見積もってしまう例がある。

*6:ただし一般化線形モデルと異なり、確率分布が推定計算の途中で出てくることはない。

*7:つまり、サンプルサイズが大きくなれば真の値に近づいていく。

*8:確率分布を使っていないので尤度に基づいた推定ではないが、擬似的に最尤法と同じ手続きを踏むことからこのような名称になっているかと思われる。

*9:具体的な分布は決めなくてもいいが、平均と分散は何らかの方法で推定できることを前提としている。

*10:総和記号の直後の偏微分は、 $\boldsymbol{\mu}_i$ の要素を $\boldsymbol{\beta}$ の要素で微分したものが並んだ行列になる。

2021-03-03

欠測データ解析としての混合モデル

反復測定データの解析欠測データの解析

はじめに

反復測定データの解析方法として、これまでCovariance pattern modelと混合モデルを紹介してきた。いずれも、目的変数の確率分布として多変量正規分布を考え、モデルのパラメータを最尤法(Maximum likelihood method)によって推定する。

最尤法を用いるこれらの方法は特に経時測定データ(Longitudinal data)で利用されることが多いのだが、広く使われている大きな理由の一つとして「目的変数に欠測(Missing)がある場合でも、一定の条件のもとであれば適切な推測ができる」という点が考えられる。というのも、経時測定データを得るためには長期間の追跡が必要であり、特に人間を対象にしたデータ（臨床検査とか、質問票とか、分野を問わず多くのものが該当する）ではデータ収集期間の途中で対象者とコンタクトがとれなくなることは日常的に起こりうるからである*1。
f:id:mstour:20210303210050j:plain

今回は、混合モデルの「欠測データの解析」という側面を掘り下げてみたい。なお、Covariance pattern modelは厳密には混合モデルとは異なるが、ここで述べる内容は全く同じように当てはまるので、今回は混合モデルだけを念頭に置いて話を進めることにする。

覚えておきたいポイント

まず最初に、実用上はこれだけ知っていればとりあえずは問題ないと思われる事柄をまとめておく。
なお、欠測メカニズムがMCARであるとは、関心あるデータが欠測するかどうかは他のいかなる変数（情報）にも影響されない、つまり欠測は完全にランダムに起こることをいう。また欠測メカニズムがMARであるとは、欠測するかどうかは「観測されている変数だけ」に影響される状態を指す。
統計学的な欠測メカニズムに関する説明は以下の記事も読んでいただけると幸いである。
mstour.hatenablog.com

欠測メカニズムがMCARまたはMARであれば、最尤法によってモデルパラメータを正しく推定することができる*2。ただし、MARの場合には欠測するかどうかを説明できる変数を全てモデルに含める必要がある。
一方、混合モデルは、治療の効果やリスク因子の影響を表すモデルパラメータを最尤法によって推定する。
したがって、経時測定データに欠測が生じている場合でも、欠測メカニズムがMCARまたはMARと想定できるのであれば（必要な変数を含んだ）混合モデルによる解析は適切である。

1.については次のセクションで詳しく見ていくが、問題点を再度確認しておこう。
データの欠測メカニズムがMCARであれば、そもそもデータに欠測のある個人を解析から除外しても、推定結果にバイアスが入らないことが知られている。例えば平均値を計算する場合、完全にランダムにいくつかのデータを計算から外したとしても大きく値が変わることは（平均的には）ない。
一方、欠測メカニズムがMARである場合、欠測に関与する情報を無視して解析すると時に大きなバイアスが入りうる。例えば日本人全体の平均身長を見積もりたいとすると、男性のデータばかりが欠測している時に単純な平均をとると、本来期待するものとはかけ離れた結果になりそうである。もし仮に欠測は「男性であること」だけが原因で起きているとすると（例えば、一部の男性だけ測定をし忘れた）、直感的には性別の情報を考慮することによって適切な推測が行えそうに思える。
性別などの変数を考慮して解析を行うとなると、使用されることが多いのは線形回帰モデル（一般化線形モデルや、混合モデルなども含めるものとする）であるが、問題は欠測データがあるような場合にパラメータの推定結果が本当に正しいのか、ということである。
結論としては、最尤法で推定する場合にはパラメータ推定結果は正しい*3ことが示されている。ただし、線形モデルの中に欠測するかどうかに関係のある変数を全て含めている必要がある*4。

2.については以前の記事でも触れた通りである。

1.と2.の事実によって、3.の通り欠測のある経時測定データの解析には混合モデルが妥当な方法であることが保証される*5。
ただし、妥当であるためには欠測に関与する変数（モデルの説明変数と、途中まで観測されている目的変数との両方を指す）がモデルに含まれていることが必要となる。

欠測メカニズムがMARの時に最尤法が適切であることの詳細

ここからは、MARの時に最尤法による推定が正当化されることの理論的背景をざっと確認していく。
ここではN人の個人に対してJ回の測定が計画された（が、一部は欠測が生じている）経時測定データ $\boldsymbol{y} = (y_1, \cdots, y_J)^T$ を解析することを考えよう*6。
これらのデータの欠測状況を示す変数（以下、「欠測指標」という）を $r_j$ で表し、 $y_j$ が観測されていれば $r_j = 1$ 、欠測となっていれば $r_j = 0$ となるよう定義する。J個の経時測定データ全ての欠測指標をまとめて $\boldsymbol{r} = (r_1, \cdots, r_J)^T$ とする。データが欠測するかどうかは事前にはわからないため、欠測指標も確率変数となる。

欠測データ解析に必要な尤度を準備する

経時測定データの確率分布*7を $f(\boldsymbol{y}|\boldsymbol{\theta})$ とする。やや抽象的な表現になっているが、正規分布を仮定するモデルを考える場合には、 $\boldsymbol{\theta}$ は平均ベクトル $\boldsymbol{\mu}$ と共分散行列 $\Sigma$ の各成分を並べたベクトルになる。
通常であれば、N人分の確率分布 $f(\boldsymbol{y}|\boldsymbol{\theta})$ の積から導出される尤度関数を最大化することによってモデルの推測を行うことができるが、欠測データを扱うためには、さらに欠測指標も合わせた確率分布を考える必要がある。

そこで、経時測定データと欠測指標との同時確率分布を $f(\boldsymbol{y}, \boldsymbol{r}|\boldsymbol{\theta}, \boldsymbol{\psi})$ とする。ただし、パラメータは経時測定データに関するパラメータ $\boldsymbol{\theta}$ と、それ以外のパラメータ $\boldsymbol{\psi}$ からなる*8。
最尤法は、確率分布（正確には確率密度関数）に実際に得られたデータの値を代入してパラメータの関数とみなした尤度関数を最大化するのであった。ところが欠測データがある場合には、一部の値が存在せず、したがって観測されたデータだけを用いて最尤法を行わなければならない。

いま、経時測定データのうち、実際に観測されたものからなるベクトルを $\boldsymbol{y}_{obs}$ 、欠測したものからなるベクトルを $\boldsymbol{y}_{mis}$ とする。また、欠測指標 $\boldsymbol{r}$ は $\boldsymbol{y}_{obs}$ と $\boldsymbol{y}_{mis}$ に対応した値をとるものとする。例えば1〜3回目の値が観測、4〜5回目の値が欠測だった場合、 $\boldsymbol{y}_{obs} = (y_1, y_2, y_3)^T$ 、 $\boldsymbol{y}_{mis} = (y_4, y_5)^T$ 、 $\boldsymbol{r} = (1, 1, 1, 0, 0)^T$ である。
欠測に対応した最尤法を行うには、経時測定データと欠測指標との同時確率分布 $f(\boldsymbol{y}, \boldsymbol{r}|\boldsymbol{\theta}, \boldsymbol{\psi})$ を「欠測したデータ $\boldsymbol{y}_{mis}$ 」に関して積分したもの：

$\displaystyle f(\boldsymbol{y}_{obs}, \boldsymbol{r}|\boldsymbol{\theta}, \boldsymbol{\psi}) = \int f(\boldsymbol{y}, \boldsymbol{r}|\boldsymbol{\theta}, \boldsymbol{\psi}) d \boldsymbol{y}_{mis} \hspace{30pt} (1)$

を最大化する。左辺に観測されたデータと欠測指標の値を代入すれば未知のパラメータの関数となるので、通常の最尤法と同様の手続きをとることができる。このようにして構成した尤度を「完全尤度(Full likelihood)」あるいは「観測データの尤度(Observed data likelihood)」という。

式(1)の完全尤度を用いることで、観測されたデータだけから推定を行うことができそうな気がするが、実際には同時確率分布 $f(\boldsymbol{y}, \boldsymbol{r}|\boldsymbol{\theta}, \boldsymbol{\psi})$ の具体的な形はわからないので（少なくとも混合モデルで想定するのは目的変数の確率分布だけである）、完全尤度をさらに分解していく必要がある。
その前に、後の展開で必要となるMARの数学的定義を確認しておこう。

MARの数学的定義

欠測指標 $\boldsymbol{r}$ の確率分布について以下が成り立つとき、データ $\boldsymbol{y}$ の欠測メカニズムはMARである。

$\displaystyle f(\boldsymbol{r}|\boldsymbol{y}, \boldsymbol{\theta}, \boldsymbol{\psi}) = f(\boldsymbol{r}|\boldsymbol{y}_{obs}, \boldsymbol{\theta}, \boldsymbol{\psi}) \hspace{30pt} (2)$

つまり、 $\boldsymbol{y}$ の各要素が欠測するかどうかの確率は、観測されたデータ $\boldsymbol{y}_{obs}$ だけに影響されることを意味する。
なお、目的変数だけではなく、さまざまな変数も欠測確率に影響を与えるようなことがありえる（むしろ、ほぼそうであると言ってよいだろう）。そのような変数の集まりを $\boldsymbol{x}$ とすると、もし $\boldsymbol{y}_{obs}$ だけでMARが成立しなくても

$\displaystyle f(\boldsymbol{r}|\boldsymbol{y}, \boldsymbol{x}, \boldsymbol{\theta}, \boldsymbol{\psi}) = f(\boldsymbol{r}|\boldsymbol{y}_{obs}, \boldsymbol{x}, \boldsymbol{\theta}, \boldsymbol{\psi})$

であれば変数の集合 $\boldsymbol{y}, \boldsymbol{x}$ に関してMARが成立する。このような場合には、例えば線形モデルの説明変数に $\boldsymbol{x}$ を含めればよい。

完全尤度の分解

では、再度、式(1)の完全尤度を見てみよう。なお以降では説明変数 $\boldsymbol{x}$ の記載は省略するが、 $\boldsymbol{x}$ で条件付けしなければMARとならないような場合にはモデルに含める必要がある。その時には、以下の展開ではそれぞれの確率分布の条件部に $\boldsymbol{x}$ が加わることになる。

条件付き確率の定義を用いると、式(1)の右辺は次のように変形できる。

$\displaystyle \int f(\boldsymbol{y}, \boldsymbol{r}|\boldsymbol{\theta}, \boldsymbol{\psi}) d \boldsymbol{y}_{mis} = \int f(\boldsymbol{y}|\boldsymbol{\theta}) f(\boldsymbol{r}|\boldsymbol{y}, \boldsymbol{\theta}, \boldsymbol{\psi}) d \boldsymbol{y}_{mis}$

さらに式(2)のMARの定義を用いると

$\displaystyle \int f(\boldsymbol{y}|\boldsymbol{\theta}) f(\boldsymbol{r}|\boldsymbol{y}, \boldsymbol{\theta}, \boldsymbol{\psi}) d \boldsymbol{y}_{mis} = \int f(\boldsymbol{y}|\boldsymbol{\theta}) f(\boldsymbol{r}|\boldsymbol{y}_{obs}, \boldsymbol{\theta}, \boldsymbol{\psi}) d \boldsymbol{y}_{mis} = f(\boldsymbol{y}_{obs}|\boldsymbol{\theta}) f(\boldsymbol{r}|\boldsymbol{y}_{obs}, \boldsymbol{\theta}, \boldsymbol{\psi})$

と変形できる。まとめると

$\displaystyle f(\boldsymbol{y}_{obs}, \boldsymbol{r}|\boldsymbol{\theta}, \boldsymbol{\psi}) = f(\boldsymbol{y}_{obs}|\boldsymbol{\theta}) f(\boldsymbol{r}|\boldsymbol{y}_{obs}, \boldsymbol{\theta}, \boldsymbol{\psi})$

である。実際の解析の場面ではN人分の尤度を用いることと（通常は異なる個人のデータは独立と仮定するので、単純にN人の尤度を掛け算する）、さらに対数をとったもの（対数尤度）を最大化するので、N人分の尤度について両辺の対数をとると

$\displaystyle \sum_{i=1}^{N} \log f(\boldsymbol{y}_{i, obs}, \boldsymbol{r}_i|\boldsymbol{\theta}, \boldsymbol{\psi}) = \sum_{i=1}^{N} \log f(\boldsymbol{y}_{i, obs}|\boldsymbol{\theta}) + \sum_{i=1}^{N} \log f(\boldsymbol{r}_i|\boldsymbol{y}_{i, obs}, \boldsymbol{\theta}, \boldsymbol{\psi})$

となる。

このように、欠測メカニズムがMARであれば完全尤度を「経時測定データに関する部分（第1項）」と「欠測指標に関する部分（第2項)」に分解することができる。経時測定データに関する部分であれば、確率分布が多変量正規分布であることを想定しているのでパラメータの推定は比較的簡単に行えそうである。

完全尤度の一部を用いれば適切な推測が可能である

長くなってきたので結論だけを述べると、完全尤度のうちの「経時測定データに関する部分」だけを用いて最尤法を行うことによって、パラメータ $\boldsymbol{\theta}$ 、つまり混合モデルであれば固定効果パラメータ・誤差の分散パラメータ・ランダム効果の分散パラメータは適切に推定できる。より正確には、

推定結果は $\boldsymbol{\theta}$ の一致推定量であり、
推定結果の従う確率分布はサンプルサイズが大きくなれば正規分布に近づく

ということが知られている。

駆け足で紹介してきたが、このような数学的背景が、欠測の可能性がつきまとう経時測定データ解析で混合モデルが広く用いられている一つの理由であるかと思う。
このように、欠測メカニズムがMARである限り、混合モデルなどの最尤法による推定を行う解析方法で関心のあるパラメータを適切に推定できることが保証されるが、そもそもMARと想定することが妥当であるかには注意が必要である。
式(2)のMARの定義について*9、左辺は

$\displaystyle f(\boldsymbol{r}|\boldsymbol{y}) = f(\boldsymbol{r}|\boldsymbol{y}_{obs}, \boldsymbol{y}_{mis}) = \frac{f(\boldsymbol{y}_{mis}|\boldsymbol{r}, \boldsymbol{y}_{obs}) f(\boldsymbol{r}|\boldsymbol{y}_{obs})}{f(\boldsymbol{y}_{mis}|\boldsymbol{y}_{obs})}$

のように変形できるので、両辺を $f(\boldsymbol{r}|\boldsymbol{y}_{obs})$ で割ることにより

$\displaystyle f(\boldsymbol{y}_{mis}|\boldsymbol{r}, \boldsymbol{y}_{obs}) = f(\boldsymbol{y}_{mis}|\boldsymbol{y}_{obs})$

となる*10。
つまり、 $\boldsymbol{y}_{obs}$ で条件付けすると、欠測が生じている変数の確率分布は欠測パターンに依存しない。
くだけた言い方をすると、欠測メカニズムがMARであると想定することは、「データに欠測がある個人の欠測した値は、データに欠測のない他のよく似た誰かとだいたい（確率的には）同じだろう」と想定していることになる。この想定が正しいかどうかは、そもそも欠測している値自体を見ることができないので、検証のしようがない。
f:id:mstour:20210303210111j:plain
この点が混合モデルをはじめとするMARを想定した解析の難点の一つだと言えるだろう*11。

まとめ

人に関するデータを経時的に測定する場合、さまざまな理由でデータの測定が途中でできなくなる可能性があるため、データの欠測という問題が避けられない。このような場合の解析方法として、混合モデルが用いられることが多くある。
今回は、混合モデルが欠測のある経時測定データに対して用いられている理論的な背景を簡単に追ってみた。一つの記事では全てを書ききれないので、関心をお持ちの方はしっかりとした書籍や論文を参考にしていただければと思うが、関連するトピックはまた随時書いていきたい。

本記事の作成に際しては、以下の資料を参考にした。
[1] 高井啓二・星野崇宏・野間久史(2016), "欠測データの統計科学", 岩波書店.
[2] 日本製薬工業協会(2016), "欠測のある連続量経時データに対する統計手法について Ver2.0".
http://www.jpma.or.jp/medicine/shinyaku/tiken/allotment/statistics.html

*1:単なる転居によって連絡がつかなくなることもあるし、研究や調査に参加するのが嫌になって拒否されてしまう場合もある。

*2:後で述べるように、厳密にはサンプルサイズが大きくなれば真の値に近づくということが保証されているということだが、統計学的にはこれで十分と考えることが多いので「正しく推定できる」と表現した。ただしサンプルサイズが小さい場合には注意が必要である。

*3:繰り返しになるが、最尤法によるパラメータ推定結果はサンプルサイズが大きくなれば真の値に収束する、というのがより正確である。このような性質を持つ推定結果は「一致推定量」と呼ばれる。

*4:MARは変数の集合に対して定義される概念であるため、例えば5つの変数でMARが成立していたとしても、そこから1つの変数を除くとMARではなくなる可能性がある。

*5:今後紹介する予定だが、正規分布を仮定できない経時測定データに対する解析方法の1つに一般化推定方程式(Generalized estimating equation; GEE)というものがある。しかし、これは最尤法を用いた推定を行わないため、混合モデルとは異なりMARの場合の妥当性は保証されない。

*6:表記を見やすくするために、個人を示すインデックス $i$ はしばらく用いないものとする。

*7:厳密には「確率密度関数」だが、直感的なわかりやすさのためにこのように表現することにする。

*8:欠測指標に関連するパラメータは $\boldsymbol{\psi}$ だけではなく $\boldsymbol{\theta}$ の一部も含む可能性があるので、「欠測指標に関するパラメータ」ではなく「それ以外のパラメータ」という表現とした。なお欠測メカニズムがMARであり、かつ欠測指標に関するパラメータが $\boldsymbol{\psi}$ のみである（つまりパラメータが「経時測定データだけに関するもの」と「欠測指標だけに関するもの」に完全に分けられる）場合を「無視可能(Ignorable)な欠測メカニズム」という。

*9:煩雑なのでパラメータの記載は省略する。

*10:説明変数 $\boldsymbol{x}$ をモデルに含める場合も同様である（条件部に入れればよい）

*11:「感度分析(Sensitivity analysis)」と称して、欠測メカニズムがMARでない（MNAR）というシナリオのもとでも結論が大きく変わらないかを検討するような事例が増えている。

2021-02-20

反復測定データのモデリング：(3)ランダム係数モデルについて少し詳しく

反復測定データの解析正規線形モデル

はじめに

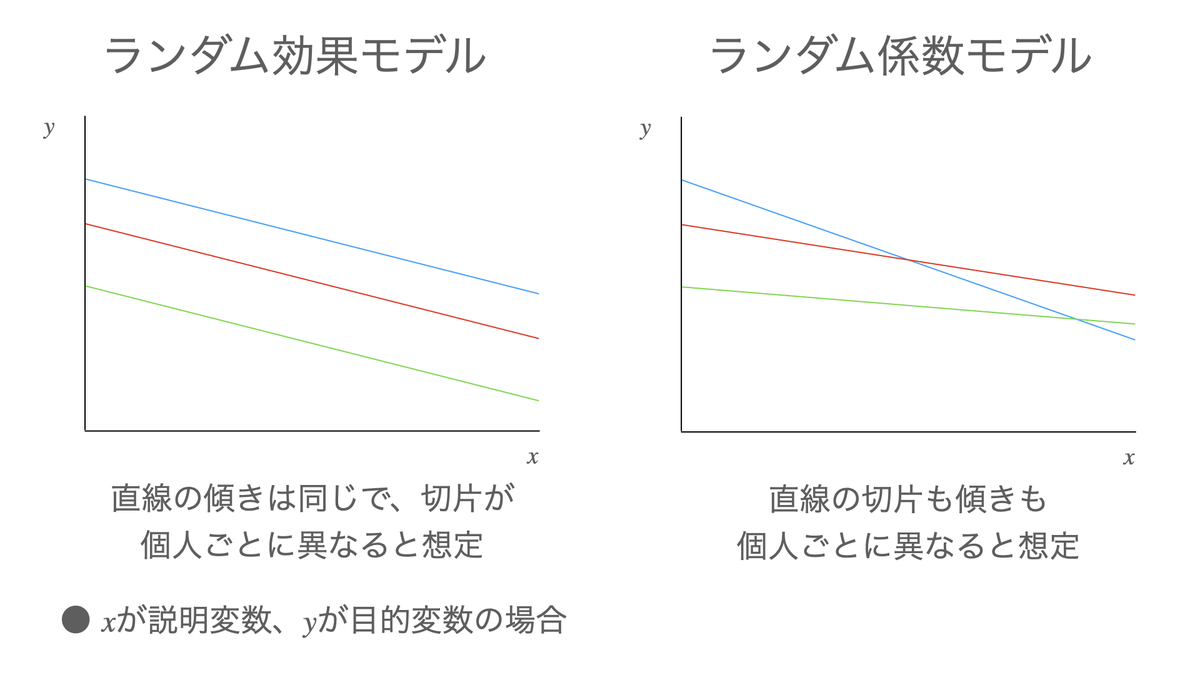
前回（反復測定データのモデリング：(2)混合モデル）は「混合モデル」の概要と、モデルの切片（目的変数に関する各個人の平均的な水準を表す）だけにランダム効果を設定する「ランダム効果モデル」についてを主に述べた。
今回は、前回説明を先送りにしていた「ランダム係数モデル(Random coefficients model)」について詳しく見ていこう。

より発展的なモデル、例えば目的変数の分布を正規分布以外に広げた「一般化線形混合モデル(Generalized linear mixed model)」や、目的変数を非線形関数によって直接モデル化する「非線形混合効果モデル(Non-linear mixed model)」といった方法も、基本的な考え方は正規分布を仮定するランダム効果モデルやランダム係数モデルと同じなので、ランダム係数モデルを知っておくと分析手法の選択肢が広がるかと思う*1。

ランダム係数モデルの概要

ランダム係数モデルとは、切片だけでなく説明変数の係数にもランダム効果を設定したモデルである。

説明のための例として、N人の個人からそれぞれT回測定した反復測定データ $y_{ij}(i = 1, \cdots, N; j = 1, \cdots, T)$ を、時間 $t_{ij}$ を説明変数としたモデルで表現する場合を考える。つまり、反復測定データと時間との関係性を直線で表現しようと試みている状況である。ランダム係数モデルはこのようなケースで用いられることが多い。なお説明変数に連続的な時間 $t_{ij}$ を含めるようなモデルであれば、反復測定を全員が同じタイミングで行っている必要はない。
まずランダム効果を全く考えないことにすると、モデルは以下の単回帰モデル

$\displaystyle y_{ij} = \beta_0 + \beta_1 t_{ij} + \varepsilon_{ij}$

になる。これは、誤差的な変動はあるものの、平均的には全ての個人が最初から最後まで同じ推移をたどることを想定していることになる。

そこでランダム効果モデル、つまり切片だけに個人差（ランダム効果）を考えることにすると

$\displaystyle y_{ij} = (\beta_0 + r_{i0}) + \beta_1 t_{ij} + \varepsilon_{ij}$

という形のモデルになる。ここでは直線の全体的な位置には個人差があることを許容しているが、直線の傾き（測定値の変化するスピード）については全員同じものとみなされている。

さらに、直線の傾き、つまり説明変数である $t_{ij}$ の係数にもランダム効果を設定すると

$\displaystyle y_{ij} = (\beta_0 + r_{i0}) + (\beta_1 + r_{i1}) t_{ij} + \varepsilon_{ij}$

となり、直線の位置も、傾きも各個人で異なるような状況を表現することができる。ランダム係数モデルはこのような形式のモデルとなる。説明変数は、通常の線形モデルと同様に複数含めてもよい。

f:id:mstour:20210220203518j:plain

ところで、前回の記事で述べたように混合モデルは一般に

$\displaystyle \boldsymbol{y} = X \boldsymbol{\beta} + Z \boldsymbol{u} + \boldsymbol{\varepsilon} \hspace{20pt} (1)$

の形式で表すことができる。
上記のランダム係数モデルをどのようにして一般形(1)で書けるかを確認しよう。
$\boldsymbol{y}$ は目的変数 $y_{ij}$ を全て並べたベクトル、同じく $\boldsymbol{\varepsilon}$ は誤差 $\varepsilon_{ij}$ を並べたベクトルであり、パラメータベクトルは $\boldsymbol{\beta} = (\beta_0, \beta_1)^T$ 、ランダム効果のベクトルは $\boldsymbol{u} = (r_{10}, r_{11}, r_{20}, r_{21}, \cdots, r_{N0}, r_{N1})^T$ （全員のランダム効果を全て並べたもの）になる。
またデザイン行列 $X$ は通常の線形モデルと同様に

$\displaystyle X = \left( \begin{array}{cccc} 1 & t_{11} \\ 1 & t_{12} \\ \vdots & \vdots \\ 1 & t_{1T} \\ 1 & t_{21} \\ \vdots & \vdots \\ 1 & t_{NT} \end{array} \right)$

であり、ランダム効果に関するデザイン行列 $Z$ は

$\displaystyle Z = \left( \begin{array}{cccc} 1 & t_{11} & 0 & 0 & \ldots & 0 & 0 \\ 1 & t_{12} & 0 & 0 & \ldots & 0 & 0 \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ 1 & t_{1T} & 0 & 0 & \ldots & 0 & 0 \\ 0 & 0 & 1 & t_{21} & \ldots & 0 & 0 \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ 0 & 0 & 0 & 0 & \ldots & 1 & t_{NT} \\ \end{array} \right)$

という形となる。

ランダム係数モデルも式(1)の一般形で表せるので、固定効果パラメータベクトル $\boldsymbol{\beta}$ は最尤法を用いて

$\displaystyle \hat{\boldsymbol{\beta}} = (X^T V^{-1} X)^{-1} X^T V^{-1} \boldsymbol{y}$

と推定できる。
また目的変数ベクトル $\boldsymbol{y}$ の分散共分散行列は

$\displaystyle V(\boldsymbol{y}) = V = Z G Z^T + R$

となる。ただし $G, R$ はそれぞれランダム効果ベクトル $\boldsymbol{u}$ と誤差ベクトル $\boldsymbol{\varepsilon}$ の分散共分散行列である*2。

ここまで、一つの説明変数の係数にランダム効果を設定した場合を考えてきたが、全く同じようにして複数の係数にランダム効果を設定することができ、同様に一般形で書き表すことができる。

応用例

今回は、教科書的な説明はそこそこにして、ランダム係数モデルの応用例を紹介したい。
事例として、「全身性強皮症に伴う間質性肺疾患」(SSc-ILD)に対するニンテダニブ(Nintedanib)の治療効果を検討したランダム化比較臨床試験を取り上げる[3][4][5]（全身性強皮症(Systemic sclerosis)については例えばこちらなどを参照されたい）。

この臨床試験は、SSc-ILD患者をニンテダニブを投与するグループとプラセボ（偽薬）を投与するグループにランダムに分け、両グループを比較することによってニンテダニブの有効性と安全性を評価したものである。有効性の主要な評価指標は「1年あたりの努力肺活量(Forced Vital Capacity; FVC)の変化量」（以下、参考資料に従い「年間減少率(Annual rate of decline)」*3とする）であり、ニンテダニブを投与することによりFVCの減少が抑えられるかどうかが検討された。
主要な評価のための解析モデルとして、ランダム係数モデルが用いられた。モデルの構造は以下の通りである。なお実際にはもっと細かな設定も必要だが、今の段階では説明不足なので省略する。

[説明変数]
投与群（ニンテダニブorプラセボ）、ATA（抗トポイソメラーゼI抗体）の有無、性別、時間、ベースライン時（投与される前）のFVC、年齢、身長、投与群と時間の交互作用、ベースライン時FVCと時間の交互作用
[ランダム効果]
切片、時間の係数

説明変数に時間を含め、ランダム効果を切片および時間に設定しているのは最初に紹介した例と同様であるが、その他にも多数の説明変数が含められている。ここで関心があるのは（横軸を時間としたときの）直線の傾きの治療群ごとの違いである。
時間変数を「年」の単位にすることによって、時間に関する係数（直線の傾き）がFVCの年間減少率の推定値になる（説明変数の係数は、その説明変数が「1単位変化した時の」目的変数の変化量を表していることに注意されたい）。また、「投与群と時間との交互作用」が、ニンテダニブを投与したグループとプラセボを投与したグループとの傾きの差（つまり、FVC年間減少率の差）にあたる。

FVC年間減少率の推定結果は以下の通りであった（資料[3][4]を元に筆者作成）。

f:id:mstour:20210220040310p:plain

この結果の算出手順を整理してみよう。

まず、上記で挙げた説明変数とランダム効果を含むランダム係数モデルをデータに当てはめた。ここで「投与群、時間、投与群と時間の交互作用」以外の説明変数を省略して記載すると、モデルは以下のように表せる：

$\displaystyle FVC_{ij} = (\beta_0 + r_{i0}) + (\beta_1 + r_{i1}) TIME_{ij} + \beta_2 DRUG_{i} + \beta_{12} TIME_{ij} \times DRUG_i + \varepsilon_{ij} \hspace{20pt} (2)$

$i$ は患者、 $j$ は測定値の通し番号を示すインデックスとする。また「FVC」は反復測定されたFVCの各値、「TIME」は $j$ 回目測定の投与開始時点からカウントした時間（単位は年）、「DRUG」は投与群（グループ）でありニンテダニブ投与のグループなら1、プラセボ投与のグループなら0をとるものとする。「TIME $\times$ DRUG」は投与群と時間の交互作用で、それぞれの変数を掛け算したものである。
このようなランダム係数モデルを用いることによって、FVCの変化には個人差があることを考慮に入れたうえで、集団全体での変化をモデリングしていることになる。

f:id:mstour:20210220203534j:plain

次に、モデルの各固定効果パラメータを最尤法で推定する*4。また、信頼区間の算出や検定を行うために必要となる、パラメータ推定量の分散も推定する（統計ソフトでは通常これらもまとめてアウトプットされる）。

推定結果から、FVCの年間減少率が算出できる。ニンテダニブ群の平均は上記のモデル式(2)のパラメータ $\beta_1$ と $\beta_{12}$ の推定値を足したもの、プラセボ群の平均はパラメータ $\beta_1$ の推定値となる。それぞれの標準誤差は、計算方法が少し複雑なので省略する。この辺りの理論的詳細はまたいずれ書きたい。
2グループの差の平均は、パラメータ $\beta_{12}$ の推定値が該当する*5。差の信頼区間の前後それぞれの幅は $\beta_{12}$ の標準誤差に（通常は）1.96を掛けた値が用いられる。

まとめ

今回は、混合モデルの紹介のところで書ききれなかったランダム係数モデルについて取り上げた。
ランダム係数モデルは、モデルの切片（つまり、目的変数の平均的な水準）だけでなく、説明変数の係数にもランダム効果を設定することによって、説明変数の効果（直線で言うと、傾き）にも個人差があることを考慮したモデルとなっている。
また医学分野での実際の応用例も紹介した*6。

今回は以下の資料を参考にした。
[1] Annette J. Dobson(2008), "一般化線形モデル入門", 共立出版.
[2] Brown and Prescott(2015), "Applied Mixed Models in Medicine", Wiley.
[3] Distler et al.(2019), "Nintedanib for Systemic Sclerosis–Associated Interstitial Lung Disease", N Engl J Med.
https://www.nejm.org/doi/full/10.1056/nejmoa1903076
（使用されたランダム係数モデルの詳細はリンク先付録のProtocolを参照。アクセスできない方には申し訳ありませんが、結果だけなら次の資料[4]の9ページ目にも記載されています。）
[4] 医薬品医療機器総合機構, "ニンテダニブエタンスルホン酸塩審査報告書".
https://www.pmda.go.jp/drugs/2019/P20191223003/530353000_22700AMX00693_A100_1.pdf
[5] Hu et al.(2021), "Power and sample size for random coefficient regression models in randomized experiments with monotone missing data", Biometrical Journal.

*1:一方、Covariance pattern modelのようにランダム効果を導入せずに正規分布以外の確率分布を扱う方法としては、一般化推定方程式(Generalized estimating equation; GEE)がよく知られている。いずれ解説を書いてみたい。

*2:ランダム効果が1個だけのランダム効果モデルとは異なり、ランダム効果が複数あるランダム係数モデルでは、同じ個人のランダム効果どうしの相関を考える必要がある。

*3:このような表現になっているのは、1年あたりの変化という「時間あたりの量」であるため「率(Rate)」であること、またFVCは疾患の進行に伴って減少していくこと、が理由だと思われる。

*4:実際には、制約つき最尤法(Restricted maximum likelihood method; REML)という推定方法を用いることが多い。

*5:端数を丸めているので、上記の表ではニンテダニブ群の平均からプラセボ群の平均を引いたものと差の平均とは少しずれている。

*6:筆者の見聞する限りでは、臨床試験でこのモデルが使われていることはそこまで多くはない。

2021-02-14

反復測定データのモデリング：(2)混合モデル

反復測定データの解析正規線形モデル

はじめに

前回は反復測定データの特徴である、同じ個人や集団から得られたデータの相関を考慮したモデリングを行うための一つの方法として、Covariance pattern modelを紹介した。Covariance pattern modelは、全ての目的変数をまとめて多変量正規分布に従う変数と考え、相関の構造も含めて線形モデルとして表現する方法と言える。

今回は、反復測定データに対するモデリングとして代表的なもう一つの方法である、混合モデル(Mixed model)を紹介する。混合モデルも、重回帰分析に代表される線形モデル（つまり、いくつかの説明変数が目的変数へ与える影響を評価する、あるいは説明変数を使って将来の目的変数の予測を行う）を拡張したものの一つである。
なお、今回もCovariance pattern modelと同様に確率分布としては正規分布のみを考えることにする*1。目的変数の従う分布として正規分布以外を考えたい場合には、一般化線形モデルを拡張した「一般化線形混合モデル(Generalized linear mixed model; GLMM)」という方法がある。

混合モデルも結果的には目的変数の分布として多変量正規分布を考えることになるわけだが、Covariance pattern modelと異なり、反復測定された目的変数1つ1つを明示的にモデリングしていく。
例えばN人の個人からそれぞれT回の測定データを得たものとする。この時、まず研究への参加者としてN人の個人が（大きな母集団からランダムに）選ばれていることを反映するため、N人の個人ごとの測定値の違いをモデルの中に取り込む。これは後で述べるように変量効果、あるいはランダム効果(Random effect)と呼ばれる。その次に、各個人のT回の測定に伴うばらつきを誤差としてモデルに取り込む。
また全体集団の中のM個の小集団（クラスター）から反復測定データを得るような場合、まずM個の小集団が（全体集団からランダムに）選ばれていることを反映するために同じくランダム効果をモデルに含める。続いて、小集団内でのばらつきを誤差としてモデルに含める。
このように反復測定データが得られた状況を踏まえたモデリングを行うことによって、データ間の相関を考慮した評価を行うことができるようになる。

混合とは？

モデルの詳細に入る前に、「混合」とはどういうことかを確認する。
といってもそう難しい話ではなくて、線形モデルを構成する（つまり、目的変数の平均を構成する）成分が「固定効果(Fixed effect)」と「ランダム効果(Random effect)」の二種類を混合したものになっている、ということを意味する。

固定効果とは？

固定効果とは、線形モデルを構成する成分のうち、ランダムにばらつかずに固定された値をとるもののことをいう。例えば以下の重回帰モデル

$\displaystyle y_i = \beta_0 + \beta_1 x_{i1} + \beta_2 x_{i2} + \varepsilon_i$

のパラメータ $\beta_0, \beta_1, \beta_2$ はいずれも確率的にばらつくことを想定しておらず、ある決められた値をとると考えている。そのため、データから最もそれらしいと思われる値を直接推定することができる*2。

上記のような重回帰モデルや一般化線形モデルは、通常は確率的に変動するものは誤差 $\varepsilon_i$ だけとされ、目的変数の平均の構成要素としては固定効果だけを含む。このようなモデルは固定効果モデルと言われることもある。

ランダム効果とは？

ただし「はじめに」で述べたように、反復測定データにおいてははそれらがランダムに選ばれた個人や集団から得られたものであることを考慮するのが望ましい。そのため、個人（あるいは集団）ごとの目的変数の値の系統的な違いをモデルに取り込みたい。
そこで、線形モデルの構成要素に、データが得られた個人ごとの違いを表す項を追加する。追加された項は、それぞれの個人がより大きな集団からランダムに選ばれたことを反映するため、ばらつきを持つ確率変数として考える。これをランダム効果と呼んでいる。

最も単純な形は、目的変数の平均的な水準に個人差があることを表現したいような場合で、単純に固定効果モデルにランダム効果を足し算する。このようなモデルは「ランダム効果モデル(Random effects model)」や「ランダム切片モデル(Random intercept model)」と表現されることがある（以下では「ランダム効果モデル」と言うことにする）。このモデルについては後ほど詳しく述べる。
また、ある説明変数の係数（つまり回帰直線の傾き）にランダム効果を追加することもできる。このようなモデルは「ランダム係数モデル(Random coefficients model)」と呼んでランダム効果モデルとは区別されることが多い。このモデルも合わせて説明すると長くなるので、また回を改めて述べることにする。
f:id:mstour:20210214203400j:plain

モデルの定式化

ランダム効果モデルについて、数式で説明する。

例として、N人の個人からそれぞれT回測定した反復測定データのモデリングを考える。個人 $i$ の $j$ 回目の測定値を $y_{ij}$ とする。
話を単純にするために、各 $y_{ij}$ を表現するモデルに説明変数は何も含めず、固定効果としては全体平均 $\mu$ だけを用いるものとする。
いま、異なる個人からそれぞれT回の測定がなされていることを反映するため、個人 $i$ の全体平均からの差（個人差）をランダム効果 $r_i$ で表す。そして、同じ個人内での測定値の誤差を $\varepsilon_{ij}$ とすると、 $y_{ij}$ は以下のランダム効果モデルで表現できる：

$\displaystyle y_{ij} = \mu + r_i + \varepsilon_{ij}$

ただし、ランダム効果 $r_i(i = 1, \cdots, N)$ は互いに独立に正規分布 $N(0, \sigma^2_r)$ に従い、誤差 $\varepsilon_{ij}(i = 1, \cdots, N; j = 1, \cdots, T)$ も互いに独立に正規分布 $N(0, \sigma^2_{\varepsilon})$ に従うものと仮定する。さらに全ての $r_i$ と $\varepsilon_{ij}$ のペアも独立とする。
このモデルは、N人の全データの平均が $\mu$ 、個人 $i$ の平均が $\mu + r_i$ であり、個人 $i$ の各測定値には $\varepsilon_{ij}$ の誤差が生じていることを示している。
f:id:mstour:20210214203420j:plain

このようにモデル化した場合の $y_{ij}$ の分散と共分散を見てみよう。
分散は、ランダム効果と誤差との独立性より全ての $i, j$ について

$\displaystyle V(y_{ij}) = V(r_i) + V(\varepsilon_{ij}) = \sigma^2_r + \sigma^2_{\varepsilon}$

共分散は、同じ個人どうしの測定値については

$\displaystyle Cov(y_{ij}, y_{iq}) = Cov(r_i + \varepsilon_{ij}, r_i + \varepsilon_{iq}) = V(r_i) = \sigma^2_r$

異なる個人どうしの測定値では

$\displaystyle Cov(y_{ij}, y_{pq}) = Cov(r_i + \varepsilon_{ij}, r_p + \varepsilon_{pq}) = Cov(r_i, r_p) = 0$

となる。したがって、同じ個人内のデータどうしについては相関があることが表現されている*3。

最後に、ランダム効果モデルだけでなくランダム係数モデルも含めた混合モデルの一般的な表現をまとめる。
前回のCovariance pattern modelでの説明と同様に、反復測定データを全て並べたベクトルを $\boldsymbol{y}$ 、誤差を全て並べたベクトルを $\boldsymbol{\varepsilon}$ とする。
モデルに含まれる全ての固定効果を $\boldsymbol{\beta}$ 、全てのランダム効果を $\boldsymbol{u}$ とすると、混合モデルは以下のように表現することができる。

$\displaystyle \boldsymbol{y} = X \boldsymbol{\beta} + Z \boldsymbol{u} + \boldsymbol{\varepsilon}$

なおランダム効果と誤差はそれぞれ多変量正規分布 $N(\boldsymbol{0}, G)$ と $N(\boldsymbol{0}, R)$ に従うものと想定する。
$X$ は固定効果に関するデザイン行列で、通常の線形モデルと同様に説明変数から構成される。
さらに $Z$ はランダム効果に関するデザイン行列であり、ランダム効果をモデルのどこに含めるかの情報を持っている。例えばこのセクションの前半で説明したランダム効果モデルの場合、ランダム効果は1個だけが足し算で加わっているので、 $Z$ は全ての要素が1のベクトルとなる。ランダム係数モデルの場合には、ランダム効果が入る（つまり、係数に個人差を考える）説明変数が $Z$ の要素に追加される。

目的変数ベクトル $\boldsymbol{y}$ の平均は、Covariance pattern modelと同様に

$\displaystyle \boldsymbol{\mu} = X \boldsymbol{\beta}$

であり、分散共分散行列は

$\displaystyle V(\boldsymbol{y}) = Z G Z^T + R$

となる*4。

固定効果 $\boldsymbol{\beta}$ の推定もCovariance pattern modelと同じく最尤法によって行うことができ、結果は以下の通りとなる。

$\displaystyle \hat{\boldsymbol{\beta}} = (X^T V^{-1} X)^{-1} X^T V^{-1} \boldsymbol{y}$

まとめ

反復測定データの（正規分布を想定した）モデリング方法の1つである混合モデルの概要を紹介した。
混合モデルでは、通常の線形モデルでパラメータとして考える「固定効果」に加えて個人差を表すための「ランダム効果」を導入することにより、同じ個人から繰り返しデータが測定されていることを反映することができる。

なお、実際の応用ではグループ間の平均に統計的に有意な差があるかどうかとか、ある説明変数が目的変数に与える影響の信頼区間などを見たいことが多くあり、そのためには固定効果の推定量 $\hat{\boldsymbol{\beta}}$ の分散を計算する必要がある。しかしながら、分散の計算には少しやっかいな問題が絡んでおり、なかなか複雑である。また次回以降に説明してみたい。

今回は以下の文献を参考にした。
[1] Annette J. Dobson(2008), "一般化線形モデル入門", 共立出版.
[2] Brown and Prescott(2015), "Applied Mixed Models in Medicine", Wiley.

*1:このような場合を参考文献[2]では「正規混合モデル(Normal mixed model)」と呼んでいる

*2:ややこしいが、パラメータの「真の値」についての話であることに注意して欲しい。最尤法や最小二乗法で求めるパラメータの「推定量」はデータをとるたびに確率的にばらつく。

*3: $y_{ij}$ と $y_{pq}$ との相関係数は共分散をそれぞれの分散の平方根で割ったものなので、 $\frac{\sigma^2_r}{\sigma^2_r + \sigma^2_{\varepsilon}}$ となる。これは「全体のばらつきのうち、個人差に起因する部分の割合」を示しており、級内相関係数(Intraclass Correlation Coefficient; ICC)と呼ばれることが多い。

*4:通常、混合モデルではランダム効果と誤差の分散共分散行列 $G, R$ のそれぞれの要素を推定する。一方、 $\boldsymbol{y}$ の（ランダム効果に関して周辺化した）分散共分散行列を $Z G Z^T + R = V$ のように $V$ としてひとまとめにすると、Covariance pattern modelと同様のモデルになる。医学研究の分野ではこのようなモデルをMMRM(Mixed Model for Repeated Measures)と呼ぶことがある。

2021-02-05

反復測定データのモデリング：(1)Covariance pattern model

正規線形モデル反復測定データの解析

はじめに

重回帰分析や一般化線形モデルといった線形モデルでは通常、異なる目的変数どうしは独立であることを仮定している。

例えば、B高校の2年生の期末テストの得点を目的変数としたい場合を考えてみると、各学生の得点どうしは独立である*1と仮定してもだいたい問題はないかと思われる。
一方で、B高校2年生であるCさんの「毎月月末に行われる学力テストの得点」についてはどうだろうか。きっと、Cさんの6月の得点と7月の得点は似たような結果になるだろう。すると、これらの得点をあたかも異なる学生の点数のように独立な値と考えるのは少し無理があると考えられる。
f:id:mstour:20210205211205j:plain

反復測定データとは

この例のように、同じ個人から時間とともに何度も繰り返し測定して得られたデータは「経時測定データ(Longitudinal data)」と呼ばれる。
また別の例として、A県内の各高校で実施された共通学力テストの結果に関心があるものとしよう。すると、入試のいわゆる偏差値が高い高校ほど学力の高い学生が集まっていることは容易に想像できるため、同じ高校の学生どうしの点数は似たようなものになると考えるのが自然である。このようにある集団内の類似した個人から得られたデータは「クラスターデータ(Clustered data)」といわれる。

経時測定データ、クラスターデータはいずれも「反復測定データ(Repeated measures data)」と表現されることが多い。つまり、ある単位（経時測定データの例では「個人」、クラスターデータの例では「特定の集団」）から何度も反復してデータを測定していることを意味しており、そのようなデータどうしには相関が生じる。
したがって、目的変数どうしに相関があることを考慮したモデルを使うことが必要となる。

いくつかの選択肢があるが、ここでは「Covariance pattern model*2」と呼ばれるモデルについて見ていこうと思う。
なおこのモデルは正規分布のデータを解析する文脈で用いられることが多いように思われるため、この記事でも同様に目的変数は正規分布に従うものとする。ただし、反復測定されたデータの相関を考慮に入れる必要があるので、データ1個1個が1変量の正規分布に従うとするのではなく、ある個人（クラスターデータの場合はある集団）の反復測定データ全てが多変量正規分布に従うと考える。

モデルの定式化

以下では、同じ個人から繰り返し測定された経時測定データで考えることにする。
いま、各個人 $i(i = 1, \cdots, N)$ について、それぞれ $n_i$ 回の反復測定がなされているとする（測定回数は個人ごとに違っていてもよい）。個人 $i$ の反復測定データ全体をベクトル

$\displaystyle \boldsymbol{y}_i = (y_{i1}, \cdots, y_{i, n_i})^T$

としてまとめ、さらにそれを全員分縦に並べたものを目的変数ベクトル

$\displaystyle \boldsymbol{y} = (\boldsymbol{y}^T_1, \cdots, \boldsymbol{y}^T_N)^T$

とする。このベクトルの長さは $M = \sum_{i=1}^{N} n_i$ であり、Covariance pattern modelでは次の（M次元）多変量正規分布に従うものと想定する：

$\displaystyle \boldsymbol{y} \sim N(\boldsymbol{\mu}, V)$

$\boldsymbol{\mu}$ は全ての個人の反復測定データ全ての平均を並べたベクトルであり、 $V$ は同じく反復測定データ全体の分散共分散行列を表す。通常は、異なる個人間の測定値は独立と想定することが多いため、以下のようなブロック対角行列を考える：

$\displaystyle V = \left( \begin{array}{cccc} V_1 & O & \ldots & O \\ O & V_2 & \ldots & O \\ \vdots & \vdots & \ddots & \vdots \\ O & O & \ldots & V_N \end{array} \right)$

$V_i(i = 1, \cdots, N)$ は個人 $i$ の測定値だけの（すなわち $\boldsymbol{y}_i$ の）分散共分散行列、 $O$ は全ての要素がゼロの行列で、つまり上記の $V$ は「同じ個人のデータどうしには相関があり」「異なる個人のデータどうしには相関がない」ことを表現している。

さて、重回帰モデルと同様に、目的変数の平均ベクトル $\boldsymbol{\mu}$ を説明変数を用いた線形モデルで表現することを考えよう。P個の説明変数をモデルに含めるものとすると、切片を含めたパラメータのベクトル

$\displaystyle \boldsymbol{\beta} = (\beta_0, \beta_1, \cdots, \beta_P)^T$

と、各個人の反復測定データに関するデザイン行列 $X_i$ を並べた行列

$\displaystyle X = (X_1^T, \cdots, X_N^T)^T$

を用いて平均ベクトルは次のように表される：

$\displaystyle \boldsymbol{\mu} = X \boldsymbol{\beta}$

なおデザイン行列は、1列目には全て1が並び（切片に対応）、2列目〜P+1列目にはそれぞれ1番目〜P番目の説明変数の値が配置される。行方向には、上から順に1回目の測定データ、2回目の測定データ、・・・、に対応する値が並ぶことになる。
簡単な例で説明する。目的変数は「6月、7月、8月それぞれの学力テストの得点」であり、説明変数として「性別を示すダミー変数（男性であれば1）」「6月であることを示すダミー変数（6月であれば1）」「7月であることを示すダミー変数（7月であれば1）」があるものとすると、男子学生 $S$ さんのデザイン行列は

$\displaystyle X_S = \left( \begin{array}{cccc} 1 & 1 & 1 & 0 \\ 1 & 1 & 0 & 1 \\ 1 & 1 & 0 & 0 \end{array} \right)$

となる。

目的変数の確率分布が特定されているので、パラメータの推定には最尤法を用いればよい（正規分布なので最小二乗法でもよい）。つまり、対数尤度をパラメータで微分する（微分したものを0に等しいとする）ことで計算することができる。
結果だけ示すと、推定量 $\hat{\boldsymbol{\beta}}$ は

$\displaystyle \hat{\boldsymbol{\beta}} = (X^T V^{-1} X)^{-1} X^T V^{-1} \boldsymbol{y}$

となる。
この式をみると目的変数ベクトルの分散共分散行列 $V$ が含まれているため、先に何らかの方法で $V$ の推定を行う必要がある。
具体的な推定方法はここでは詳しく述べないことにするけれど、その前の話として、重回帰モデルなどと異なり分散パラメータが1つではないため、まずは $V$ の具体的な形を決めてあげなければならない。分散共分散行列の具体的な形は「共分散構造(Covariance pattern)」と呼ばれる。

共分散構造

共分散構造を決めるとは、つまり、「同じ個人の反復測定データどうしがお互いにどういう関係性にあると考えられるか」をある程度事前に決めておくということである。具体的な推定値はデータから計算するわけだが、その構造はモデルの定義としてあらかじめ決めておかないと話が先に進まない*3。
例えば、6月の成績と7月の成績はほとんど同じになるけれど、6月の成績と12月の成績はほとんど関係がないかもしれない。そういうことが事前の知識から予想できるのであれば、そのことを共分散構造に反映させることでより適切なモデル化ができるだろう。

共分散構造として、以下のものが比較的よく使われる。
なお、実用的には全ての個人で分散共分散行列 $V_i$ は同じと考えることが多いので*4、以下では $V_i$ を代表として表記する。全体の分散共分散行列は同じ $V_i$ を対角線上に並べたものになる。

(1) Unstructured （Generalとも呼ばれる）
これは、全てのデータ間の共分散と全てのデータの分散が異なることを許容する、最も制約の弱い構造である。

$\displaystyle V_i = \left( \begin{array}{ccccc} \sigma^2_1 & \theta_{12} & \theta_{13} & \ldots & \theta_{1, n_i} \\ \theta_{12} & \sigma^2_2 & \theta_{23} & \ldots & \theta_{2, n_i} \\ \theta_{13} & \theta_{23} & \sigma^2_3 & \ldots & \theta_{3, n_i} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ \theta_{1, n_i} & \theta_{2, n_i} & \theta_{3, n_i} & \ldots & \sigma^2_{n_i} \end{array} \right)$

したがって、最も柔軟にデータにフィットしたモデル化ができるが、測定回数が増えるとパラメータ数が膨れ上がってしまうため、推定が不可能になる（反復計算を行うので、計算が収束しなくなる）恐れがある。
そのため、計算が収束しなかった場合にはより単純な構造を採用する、といったオプションを前もって決めておくこともよく行われる。

(2) Toeplitz
Unstructuredよりも制約を強くして、全てのデータの分散は等しく、また測定の間隔が同じデータの組（例えば、6月と7月の成績と、8月と9月の成績）の共分散（したがって相関も）は全て同じであるとする。

$\displaystyle V_i = \left( \begin{array}{ccccc} \sigma^2 & \theta_{1} & \theta_{2} & \ldots & \theta_{n_i -1} \\ \theta_{1} & \sigma^2 & \theta_{1} & \ldots & \theta_{n_i -2} \\ \theta_{2} & \theta_{1} & \sigma^2 & \ldots & \theta_{n_i -3} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ \theta_{n_i -1} & \theta_{n_i -2} & \theta_{n_i -3} & \ldots & \sigma^2 \end{array} \right)$

隣りあう時点のデータどうしよりもお互いに離れたデータどうしの方が関連性が薄くなるというケースはよくあると考えられる。Toeplitz型はUnstructuredほどの柔軟性はないが、そのことを反映できる構造になっている。
f:id:mstour:20210205211228j:plain

(3) First-order autoregressive
この構造もToeplitzと同じくデータの間隔が異なれば関連性も異なると想定しているが、下記のように制約はかなり強くなっている：

$\displaystyle V_i = \left( \begin{array}{ccccc} \sigma^2 & \sigma^2 \rho & \sigma^2 \rho^2 & \ldots & \sigma^2 \rho^{n_i -1} \\ \sigma^2 \rho & \sigma^2 & \sigma^2 \rho & \ldots & \sigma^2 \rho^{n_i -2} \\ \sigma^2 \rho^2 & \sigma^2 \rho & \sigma^2 & \ldots & \sigma^2 \rho^{n_i -3} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ \sigma^2 \rho^{n_i -1} & \sigma^2 \rho^{n_i -2} & \sigma^2 \rho^{n_i -3} & \ldots & \sigma^2 \end{array} \right)$

$\rho$ は隣りあうデータどうしの相関係数であり、相関係数は-1から1までの範囲の値をとるため、測定の間隔が離れれば離れるほど関連性が薄くなっていくことを表現できる。

(4) Compound symmetry
異なる測定時点のデータどうしの関連性は全て同じであるとする構造であり、非常に強い制約を置いている。

$\displaystyle V_i = \left( \begin{array}{ccccc} \sigma^2 & \theta & \theta & \ldots & \theta \\ \theta & \sigma^2 & \theta & \ldots & \theta \\ \theta & \theta & \sigma^2 & \ldots & \theta \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ \theta & \theta & \theta & \ldots & \sigma^2 \end{array} \right)$

過度に複雑な構造よりも推奨されることもあるが、上記(1)〜(3)のようにデータの間隔によって関連性が変わってくる様相は捉えられないので、この構造でよいかどうかは慎重に考えた方がいいかもしれない。

まとめ

同じ個人や、特定の同質な集団から測定された反復測定データは互いに相関が生じる。そのような場合にデータどうしを独立であると仮定する通常の回帰分析は適切とはいえないため、相関があることを考慮したモデルが必要である。
その一つであるCovariance pattern modelは、データの集まりの従う確率分布として多変量正規分布を想定し、データどうしの関連性（分散共分散行列）の構造も含めてモデル化を行う方法である。
これによって、通常の回帰分析と同様に説明変数が目的変数へ与える影響を評価することができる。

今回は以下の文献を参考にした。
[1] Annette J. Dobson(2008), "一般化線形モデル入門", 共立出版.
[2] Brown and Prescott(2015), "Applied Mixed Models in Medicine", Wiley.

*1:以下、統計学的な意味での「独立」を意味するものとする。ざっくりいうと、一方の値が他方の値とは全く関係しないということを指す

*2:適切な日本語訳がなさそうなので、英語での表現を用いることにする

*3:もちろん一つの共分散構造に決めうちする必要はなくて、たくさんの候補の中から最も適切なものをAICなどの基準によって選ぶということも普通に行われている。ただしその場合でも、候補をあらかじめ特定しておかなければ何もできない

*4:全ての個人で異なるとすると、推定すべきパラメータの数が膨大になる

2021-01-28

一般化線形モデルの一般論

一般化線形モデル

はじめに

これまで、単回帰分析や重回帰分析といった「目的変数が正規分布に従う」と想定する線形モデルについて説明してきた。
しかしながら、関心のあるデータはいつも正規分布だけで表現できるわけではない。ある病気になるリスクを高くしたり低くしたりする要因について考察したい場合もあるし、発作の回数に影響する要因を探りたいような場合もある。
一般に、ある病気になるか・ならないかはBernoulli（ベルヌーイ）分布*1、発作の回数であればPoisson（ポアソン）分布が適切とされることが多い。

統計モデルはそもそも現実を単純化して表現したものにすぎないが、データの性質に合わせた確率分布を用いることができれば、現実を理解するための助けになるはずである。
そこで、正規分布の線形モデル*2を他の確率分布を扱えるように拡張した「一般化線形モデル(Generalized linear model)」という枠組みが開発されてきた（といっても、提案されたのはもう50年くらい前のことらしい）。

正規分布の線形モデルと何が違うのか

正規分布の線形モデルと違う点は、大きく2つある。

(1) 正規分布以外の確率分布を扱える。

「はじめに」で述べた通り、2値のデータに対してはBernoulli分布、計数データ（0, 1, 2, ...のように自然数の値をとるデータ）に対してはPoisson分布を用いるなど、目的変数の従う確率分布として正規分布以外にも選択肢を広げることができる。

f:id:mstour:20210128193911j:plain
なおBernoulli分布やPoisson分布など、一般化線形モデルで扱うことのできる確率分布は「指数型分布族(Exponential family of distributions)」と呼ばれるグループに属する。

指数型分布族とは大雑把にいうと、確率密度関数（離散的分布の場合は、確率関数）を数学的に式変形することで、ある共通の形式に書き直すことができるような確率分布をまとめたもののことをいう。詳しい話は、また機会があれば書きたいと思う。
この指数型分布族に属する確率分布であれば、どのような分布を想定した場合でも同じ手順によってパラメータの推定、信頼区間の推定、パラメータに関する検定が行えるよう、理論的に整備されている。

(2) 目的変数と説明変数との関係性が、非線形になりうる。

正規分布の線形モデルの場合、目的変数の期待値（すなわち、正規分布の平均パラメータ）と説明変数とが次のような形式で等式で結びつけられていた*3。

$\displaystyle E(y_i) = \mu_i = \boldsymbol{x}_i^T \boldsymbol{\beta}$

正規分布に従う確率変数はあらゆる実数値をとりうるので（ $-\infty$ から $\infty$ まで）、説明変数にどんな値が入っても特に問題はなかったが、その他の確率分布を用いる場合には問題が生じる。
例えば、Bernoulli分布のパラメータは「値が1となる確率 $\pi$ 」なのだが、 $\pi$ は確率なので0〜1の値しかとることができない。ところが正規分布の場合と同じように

$\displaystyle \pi_i = \boldsymbol{x}_i^T \boldsymbol{\beta}$

としてしまうと、説明変数 $\boldsymbol{x}$ の値によっては0〜1の範囲をはみ出してしまうことになる。

そこで、左辺の $\pi_i$ を次のように変換する。

$\displaystyle \log \left( \frac{\pi_i}{1-\pi_i} \right) = \boldsymbol{x}_i^T \boldsymbol{\beta}$

このような変換を施すと、左辺は $-\infty$ から $\infty$ までの全ての実数値をとることができるようになる。例えば $\pi_i = 0$ の場合（厳密には0に近づけた場合の極限）には左辺は $-\infty$ となり、 $\pi_i = 1$ の場合（同じく極限）には左辺は $\infty$ となる。 $\pi_i$ を0から1の方向へ動かせば、それに伴って左辺も $-\infty$ から $\infty$ の方向へ単調に増加する。
f:id:mstour:20210128193933p:plain
この変換によって、説明変数 $\boldsymbol{x}_i$ とパラメータ $\pi_i$ との間には非線形な関係が生じることになる。なお $\pi_i$ を $\log \left( \frac{\pi_i}{1-\pi_i} \right)$ へ変換する関数は「ロジット関数(Logit function)」と呼ばれる。

モデルの標準形

上記の例のように、一般化線形モデルでは、目的変数が従うと想定した確率分布のパラメータと説明変数とを適切に結びつけるために、「パラメータを非線形関数で変形したもの」と説明変数とを等式で結びつける。
モデル化すべきパラメータを $\theta_i$ とすると、一般的な形式は次のようになる。

$\displaystyle g(\theta_i) = \boldsymbol{x}_i^T \boldsymbol{\beta}$

適切に変換するための関数 $g$ は「連結関数(Link function)」と呼ばれる。
この連結関数は使用する確率分布によって適切なものがほぼ決まっており、対応する確率密度関数を式変形することで導出することができる（このあたりの話はまた改めて）。
なお、連結関数 $g$ は単調（つまり、引数 $\theta_i$ の値が大きくなれば常に関数値 $g(\theta_i)$ の値も大きくなる）で、かつ微分可能であるものが用いられる。

具体例をいくつか挙げる。
目的変数の分布として正規分布を想定したモデルでは連結関数 $g$ は恒等関数、つまり何も変換しないという関数を用いていることになる：

$\displaystyle g(\mu_i) = \mu_i = \boldsymbol{x}_i^T \boldsymbol{\beta}$

Bernoulli分布を想定する場合は、前述のロジット関数

$\displaystyle g(\pi_i) = \log \left( \frac{\pi_i}{1-\pi_i} \right) = \boldsymbol{x}_i^T \boldsymbol{\beta}$

が連結関数である。このモデルはロジスティック回帰(Logistic regression)としてよく知られている。

Poisson分布を想定する時は、分布を特徴づけるパラメータである $\lambda_i$ に関して

$\displaystyle g(\lambda_i) = \log \left( \lambda_i \right) = \boldsymbol{x}_i^T \boldsymbol{\beta}$

のように対数関数が連結関数となる*4。

まとめ

一般化線形モデルや関連するモデルを紹介していくにあたり、まずは一般化線形モデルと正規分布モデルとの違いを大まかに述べた。
大きな違いは、
・目的変数をモデル化するために、指数型分布族に属するさまざまな確率分布を使用することができる
・説明変数と目的変数（の従う分布のパラメータ）との間を連結関数で結ぶことにより、説明変数がどのような値であってもパラメータのとりうる値の範囲から逸脱することがない
という点である。
今後は、重要な個々のモデルの紹介や、理論的背景に話を進めていければと思う。

今回は以下の文献を参考にした。
[1] Annette J. Dobson(2008), "一般化線形モデル入門", 共立出版.
[2] John M. Lachin(2020), "医薬データのための統計解析", 共立出版.

*1:2値データの解析では病気になった人数について二項分布を考えることが多いが、ここでは各個人が病気になるorならない、の分布を考えている

*2:重回帰分析、分散分析、共分散分析といった正規分布の線形モデルは「一般線形モデル(General linear model)」と総称されることがあるが、一般化線形モデルと紛らわしいのでここではこの用語は使わなかった

*3:単回帰や重回帰の説明では「目的変数の（説明変数を与えたもとでの条件付き）期待値をモデル化する」という流れで話をしたが、他の分布を使う際にはパラメータに対するモデル式を立てていくと考えるほうが理解しやすいので、以降はそのような言い方をすることにする

*4:目的変数である「何らかの事象の発生回数」が観察時間や観察個体数などに依存するような場合には上式の右辺に「オフセット項」を含めることがあるが、ここではその話は省略した

2021-01-22

交互作用を表現する線形モデルをRで実施する

R 正規線形モデル一般化線形モデル

はじめに

前回の記事で交互作用の概念について説明したが、その続きとして、シミュレーションデータを使ってRでの実行例を見ていきたいと思う。
mstour.hatenablog.com

なお今回は2値のカテゴリー変数どうしの交互作用だけを扱うことにする。
問題設定は次の通りである。
目的変数（結果側の変数）として期末テストの得点、説明変数として補習を受けたかどうか（補習あり or 補習なし）と性別（男子学生 or 女子学生）のデータがあり、テストの得点に対する補習の効果を見たいものとする。

補習の効果と性別との交互作用がないケース・あるケースそれぞれのサンプルデータを作成し、線形回帰モデルを実行して結果を見ていくことにしよう。

交互作用のないケース

最初に、補習の効果と性別とには交互作用がないようなデータを作成する。

#----- 前準備 -----
library(tidyverse)
library(truncnorm)
set.seed(992)
n = 300

ここで、テストの得点の生成に「切断正規分布」を利用するためにtruncnormパッケージを読みこんでいる。切断正規分布とは、ランダムサンプルのとりうる値をある範囲に制限した正規分布のことで、以下で0から100までの値しか生成されないように設定している。

#----- 各変数の作成 -----
# ID
ID = 1:n

# Group
Hosyu = c(rep("Y", n/2), rep("N", n/2))
# Hosyu dummy
Hosyu_Y = rep(0, n)
Hosyu_Y[Hosyu == "Y"] = 1

# Gender
Gender = c(rep("M", n/4), rep("F", n/4), rep("M", n/4), rep("F", n/4))
# Male dummy
Gender_Male = rep(0, n)
Gender_Male[Gender == "M"] = 1

# Final exam. score (No interaction)
Score1 = round(rtruncnorm(n, a = 0, b = 100, mean = 30, sd = 10)
 + Hosyu_Y * 20 + Gender_Male * (-10), 0)

#----- データフレーム作成 -----
ad1 = data.frame(ID = ID, Hosyu = Hosyu, Gender = Gender, 
 Hosyu_Y = Hosyu_Y, Gender_Male = Gender_Male, Score = Score1)

補習については補習ありの場合に1・なしの場合に0をとるダミー変数を、性別については男子学生の場合に1・女子学生の場合に0をとるダミー変数をそれぞれ用意している。
テストの得点は、補習の有無と性別の両方から影響を受けるが、両者の交互作用はないようにデータを生成している。
最後に各変数をデータフレームにまとめる。

以下のコードで、補習あり・なしそれぞれのグループのテスト得点の平均値を可視化してみる。

#----- プロット作成用に、補習の有無および性別ごとの平均値を算出 -----
ad1summary = summarise(group_by(ad1, Gender, Hosyu), m = mean(Score))
ad1summary$Hosyu_Y = c(0, 1, 0, 1)

#----- 平均値をプロットする -----
ggplot(ad1summary, aes(x = Hosyu_Y, y = m, color = Gender)) +
  geom_line() + geom_point() +
  scale_x_continuous(breaks = c(0, 1), labels = c("Nashi", "Ari")) +
  xlab("Hosyu") + ylab("Final exam score")

通常、2値の変数を使ってこのような折れ線グラフを描くことはあまりないと思うが、前回の話の流れと繋がりやすくするためにあえて作成した。横軸の「補習あり・なし」にはダミー変数を使っているが、ラベルを細工してカテゴリー型変数っぽくしている。
プロットは以下のようになる。
f:id:mstour:20210119210518p:plain
緑色の直線の傾きが男子学生の補習の効果、赤色の直線の傾きが女子学生の補習の効果を示している。直線はほとんど平行であり、補習の効果と性別とに交互作用はなさそうなことが分かる。

さて、まずはこのデータに「交互作用項を含めた線形回帰モデル」（補習と性別とに交互作用があると仮定したモデル）を当てはめることにする。

lm1_int = lm(Score ~ Hosyu_Y + Gender_Male + Hosyu_Y*Gender_Male, data = ad1)
summary(lm1_int)

結果は以下のようになった。
f:id:mstour:20210121201139j:plain
赤線で示す部分が交互作用項の係数の推定を表しているが、p値（「係数が0である」という帰無仮説に対応する）を見る限り、交互作用があることを積極的に示すような結果にはなっていない*1。

次に、「交互作用項を除いた線形回帰モデル」（交互作用がないと仮定したモデル）を当てはめてみよう。

lm1_noint = lm(Score ~ Hosyu_Y + Gender_Male, data = ad1)
summary(lm1_noint)

f:id:mstour:20210121201151j:plain
補習の効果の推定値（Estimate）は、交互作用項を含めたモデルとほぼ同じになった（交互作用項を含んだモデルでは、係数の推定値が0に近かったため）。
交互作用項を含めるべき理由は特に見当たらないため、今回のデータに関しては、交互作用項のないこちらのモデルで十分だろう。

続いて、交互作用のあるようなデータを作ってみよう。

交互作用のあるケース

説明変数については先ほど作成したものを流用して、テストの得点のみ、補習と性別とに交互作用が生じるような設定で新たに作成する。

# Final exam. score (Interaction Gender*Hosyu)
Score2 = round(rtruncnorm(n, a = 0, b = 100, mean = 30, sd = 10)
 + Hosyu_Y * 15 + Gender_Male * (-10) + Gender_Male * Hosyu_Y * 10, 0)

#----- データフレーム作成 -----
ad2 = data.frame(ID = ID, Hosyu = Hosyu, Gender = Gender,
                 Hosyu_Y = Hosyu_Y, Gender_Male = Gender_Male, Score = Score2)

先ほどと同様にプロットしてみよう。

#----- プロット作成用に、補習の有無および性別ごとの平均値を算出 -----
ad2summary = summarise(group_by(ad2, Gender, Hosyu), m = mean(Score))
ad2summary$Hosyu_Y = c(0, 1, 0, 1)

#----- 平均値をプロットする -----
ggplot(ad2summary, aes(x = Hosyu_Y, y = m, color = Gender)) +
  geom_line() + geom_point() +
  scale_x_continuous(breaks = c(0, 1), labels = c("Nashi", "Ari")) +
  xlab("Hosyu") + ylab("Final exam score")

f:id:mstour:20210120200235p:plain
直線は平行になっておらず、男子学生と女子学生とで補習の効果が大きく異なっていることが分かる。

交互作用のないシミュレーションデータと同じように、まずは「交互作用項を含めた線形回帰モデル」によるモデリングを行ってみよう。

lm2_int = lm(Score ~ Hosyu_Y + Gender_Male + Hosyu_Y*Gender_Male, data = ad2)
summary(lm2_int)

f:id:mstour:20210121201206j:plain
補習と性別との交互作用項に関する推定結果を見ると、「Estimate」が7.96となっている。この項は男子学生と女子学生との補習効果の差を示しており、男子学生は女子学生よりも補習の効果がおよそ8点大きいと推定されている。
また係数についてのp値は非常に小さく、交互作用があることが強く示唆される結果となっている。

同様に「交互作用項を除いた線形回帰モデル」も当てはめてみる。

lm2_noint = lm(Score ~ Hosyu_Y + Gender_Male, data = ad2)
summary(lm2_noint)

f:id:mstour:20210121201217j:plain
交互作用項を含むモデルと比較すると、補習の効果が4点程度大きくなっている。
これは、本来は男女で異なっているはずの補習の効果（交互作用ありのモデルからは、男子学生の効果は15.68 + 7.96 = 23.64、女子学生の効果は15.68と推定されている）を、男女で平均した結果となっている（(23.64 + 15.68) / 2 = 19.66）*2。

対象母集団全体での補習の効果を見積もりたい場合には交互作用項のないモデルで問題はないが、データを正確にモデリングすることが目的であれば、このようなケースでは交互作用項を含めたモデルを用いるほうがよいだろう。

まとめ

交互作用項を含めた線形回帰モデルのRでの実行について、交互作用のある場合・ない場合それぞれのシミュレーションデータを用いて説明した。
今回のデータ例において、交互作用項のあるモデルは男女別に回帰モデルを当てはめるのと同じようなことを行っている（厳密には異なる）。
Rでのプロット作成に関しては、以下の資料を参考にした。
[1] グラフ頂上決戦　もしも、SASのsgplotとRのggplot2を比較したら・・・
http://nfunao.web.fc2.com/files/sgplot_vs_ggplot2.pdf
[2] Mukku John Blog：ggplot2を使って、軸を制御する-3
http://mukkujohn.hatenablog.com/entry/2016/10/11/220722

*1:p値が大きいから交互作用がない（逆にp値が小さければ交互作用がある）、と断定できるわけではないが、一つの目安としては考えてもよいかと思う

*2:今回は男女の人数が同じなのでこのような結果になっているが、例えば男子学生の人数が多い場合には、交互作用項のないモデルの補習の効果は23.64により近くなる

2021-01-13

線形モデルにおける交互作用

正規線形モデル一般化線形モデル実験計画法

はじめに

前回の「ダミー変数」についての記事の最後に、連続型とカテゴリー型の説明変数が混在した線形モデルが登場した。
mstour.hatenablog.com
このようなモデルを模式的に図解すると、縦軸に目的変数の値(点数）、横軸に連続型変数（学習時間）の値が置かれ、各カテゴリー（受けた補習のグループ）の平均を示す直線*1が平行に並び、直線間の長さがグループ間の差を示している。
また直線の傾きが、学習時間が増えるにともなって点数が上昇する程度を表す。

ところで、この「直線の傾き」に注目していただきたい。
f:id:mstour:20210108202446j:plain

ここには暗黙のうちにとても大きな仮定が置かれていることにお気づきだろうか。

その仮定とは、「3つの全ての直線が平行であること」*2。
つまり、補習を受けていないグループも、放課後だけ補習を受けたグループも、放課後だけでなく始業前も補習を受けたグループも、学習時間を増やすことによるテストの点数の伸び具合が全く同じだと仮定されている。
そのように考えられる十分な根拠があるなど、この仮定を正当化できる理由があればよいが、例えば次の図のような関係性のほうがより適切なモデルになっているかもしれない。
f:id:mstour:20210113204202j:plain
このモデルでは、補習を受ける量が増える（なし＜放課後のみ＜放課後+始業前）につれて、直線の傾きが急になっている。つまり、補習を受ける量が多くなるほど、少ない家庭学習時間でより高得点を取れるようになるという様子を表している。十分にありえるのではないだろうか？

このように、グループによってある説明変数の効果が異なるような時、グループとその説明変数との間には「交互作用(Interaction)が存在する」と表現される。
交互作用を無視するとデータを誤って解釈してしまう危険があるので、交互作用を線形モデルに取り入れるべき場面がある。今回は、線形モデルにおいて交互作用をどう取り扱うかについて話していきたい。

交互作用とは

教科書的に言うと、交互作用とは、「ある要因の効果は一定ではなく、他の要因の水準によって異なっている」ような状況を指す。このことを、もう少し単純な例で説明してみよう。

いま、補習を受けた場合と受けなかった場合を比較して、期末テストの点数に違いがあったかを確かめたいものとする（補習のカテゴリーは、「あり」と「なし」の2つである）。
ここで、男子学生と女子学生とで補習の効果に違いはあるだろうかという疑問がわいたとしよう。
そこで、男女別に補習を受けた学生と受けなかった学生の点数の平均をそれぞれ計算してみたところ、男子学生の方が女子学生よりも補習による点数の伸びが大きかったことが判明した*3。
f:id:mstour:20210113204219j:plain
この時、補習の効果は一定ではなく、性別によって異なっていることから、補習と性別との間には交互作用が存在していることになる。

なおここでは交互作用のある変数として2カテゴリーだけからなる変数（補習、性別）を例示したが、一方の変数が連続型の場合も考え方は全く同様である（「はじめに」での例の通り）。

線形モデルで交互作用をどう表現するか

では、このような交互作用がありそうだとして、線形モデルでどのように表現すればよいか？
「補習のあり・なし」と「性別」の単純な例で考えてみる。

目的変数であるテストの点数を $y_i$ 、補習のあり・なしを $x_{i1}$ 、性別を $x_{i2}$ とする。ただし $x_{i1}$ は補習ありのとき1、補習なしのとき0をとるものとする。同様に、 $x_{i2}$ は男子学生の場合に1、女子学生の場合に0をとるものとする。まず、補習のあり・なしと性別を説明変数とする線形モデル*4は

$\displaystyle y_i = \beta_0 + \beta_1 x_{i1} + \beta_2 x_{i2} + \varepsilon_i \hspace{20pt} (i = 1, \cdots, N)$

と表せる。
いま関心があるのは補習を受けた時の効果なので、「補習ありのグループと、補習なしのグループとの差」である $\beta_1$ の値がどのくらいになるかを知りたい。
なお、説明変数に $x_{i2}$ を含めることによって、男女間の差（補習の効果とは関係のない、元々の学力の違い）を調整している*5。したがってこのモデルでは、男女間の元々の学力の違いによる影響を取り除いた上で、補習の効果を評価することを意図している。

しかしながら、このモデルでは「男子学生と女子学生とで、補習の効果は同じ」と仮定していることになるため、交互作用を反映するにはモデルの修正が必要となる。
交互作用を反映させるには、以下のように $\beta_3 x_{i1} x_{i2}$ という項を追加する（ $x_{i1} x_{i2}$ は、 $x_{i1}$ と $x_{i2}$ との掛け算であることに注意されたい）。

$\displaystyle y_i = \beta_0 + \beta_1 x_{i1} + \beta_2 x_{i2} + \beta_3 x_{i1} x_{i2} + \varepsilon_i \hspace{20pt} (i = 1, \cdots, N)$

このようなモデルをあてはめると、男子学生の補習の効果は「 $x_{i1} = 1, x_{i2} = 1$ の場合」から「 $x_{i1} = 0, x_{i2} = 1$ の場合」を引けばよいので

$\displaystyle (\beta_0 + \beta_1 + \beta_2 + \beta_3) - (\beta_0 + \beta_2) = \beta_1 + \beta_3$

女子学生の補習の効果は「 $x_{i1} = 1, x_{i2} = 0$ の場合」から「 $x_{i1} = 0, x_{i2} = 0$ の場合」を引けばよいので

$\displaystyle (\beta_0 + \beta_1) - (\beta_0) = \beta_1$

となる。つまり、交互作用項のパラメータ $\beta_3$ が、男女間の補習の効果の違いを表している。
f:id:mstour:20210113204238j:plain

最後に連続型の変数との交互作用についても触れておく。
「補習のあり・なし」と「家庭での学習時間」とに交互作用があるとする場合を考えてみよう。先ほどと同様に補習のあり・なしを $x_{i1}$ とし、家庭での学習時間を $x_{i2}$ とする。
この場合も交互作用項としては $\beta_3 x_{i1} x_{i2}$ を追加して

$\displaystyle y_i = \beta_0 + \beta_1 x_{i1} + \beta_2 x_{i2} + \beta_3 x_{i1} x_{i2} + \varepsilon_i \hspace{20pt} (i = 1, \cdots, N)$

というモデルを用いればよい。
この場合の補習の効果を先ほどと同様に「 $x_{i1} = 1$ の場合」から「 $x_{i1} = 0$ の場合」を引く形で計算してみると

$\displaystyle (\beta_0 + \beta_1 + \beta_2 x_{i2} + \beta_3 x_{i2}) - (\beta_0 + \beta_2 x_{i2}) = \beta_1 + \beta_3 x_{i2}$

となり、家庭での学習時間 $x_{i2}$ によって値が変わってしまう。したがって、このような交互作用が考えられる場合には、全体で共通の補習の効果は計算できず、例えば「家庭学習時間が30分の場合の補習の効果は・・・」のような個々の効果を評価することになる。
f:id:mstour:20210113204252j:plain

まとめ

交互作用の概念と、線形モデルにおける交互作用の表現について紹介した。
実際にデータと解析例を見るとよりわかりやすいけれど、長くなるので、改めてRを用いたシミュレーションを記事にしたいと思う。

今回は以下の文献を参考にした。
[1] J.L.Fleiss(2004), "臨床試験のデザインと解析", アーム.
[2] John M. Lachin(2020), "医薬データのための統計解析", 共立出版.
[3] David W. Hosmer他(2014), "生存時間解析入門", 東京大学出版会.

*1:説明変数に学習時間を入れているので、平均は学習時間によって変動する。

*2:いわゆる共分散分析も、このことを仮定している。

*3:なお、話を単純にするために、補習を受けなかった学生の点数の平均は男女で同じだったとする。

*4:ここでは目的変数に正規分布を仮定した重回帰モデルを用いているが、一般化線形モデルやCox比例ハザードモデルなどでも以降の考え方は同様である。

*5:「交互作用とは」のところでは男女間の元々の違いはないものと単純化していたが、ここではより一般的なケースを考えている。なお補習を受ける・受けないをランダムに割り当てる「ランダム化比較試験」を行えば、補習ありのグループと補習なしのグループの男女比は平均的に等しくなるので、男女間の違いをそれほど厳格に調整しなくてもよい。ただし、性別が結果に非常に強く影響を及ぼすと想定される場合には、ランダム化の際に層別化したり、解析の段階で調整を行ったりする場合も多い。