2値データの解析：(4)Mantel-Haenszel検定

はじめに

以前、Mantel-Haenszel検定についてたまたま関連する論文を読んでいたので記事を書いた。
mstour.hatenablog.com
当時ははっきり言って取り留めなくつらつらと書いただけなので、改めてきちんと説明していこうと思う。
なおこの記事でも触れたように、Cochranが提案した方法とMantel and Haenszelが提案した方法は少し異なるが、構成した検定統計量は漸近的に同じになるので、まとめてCMH検定と呼ばれることが多い。統計ソフトではCMH検定と言いつつ暗にMantel-Haenszelタイプの方法を行っているようなので、ややこしい。したがってこの記事ではMantel-Haenszel検定（長いので、以降はMH検定とする）で統一することにする。

Mantel-Haenszel検定は何をしているのか

MH検定は「層別解析」を行う方法としてよく用いられている。なお、 $2 \times 2$ 分割表の場合で、かつ層の数が1（つまり層別しない）のときにはMH検定のカイ二乗統計量 $\chi_{MH}^2$ とPearsonのカイ二乗統計量 $\chi_{P}^2$ はほぼ等しい（Busing et al.(2016)）：

$\displaystyle \chi_{MH}^2 = \frac{N-1}{N} \chi_{P}^2$

このとき、 $\chi_{MH}^2$ も $\chi_{P}^2$ も自由度1のカイ二乗分布に漸近的に従う。したがって、MH検定はPearsonカイ二乗検定を層別解析に拡張したものというふうに整理してもよいかと思う。
介入（例えば、異なる2つの治療）や曝露（例えば、喫煙などのリスク因子）が結果に与える影響を評価したい場合に、結果へ影響するその他の要因が邪魔をするようなことが非常に多い。例として、「筋トレをすれば社会的に成功する」ことを実証したいものとしよう。結論から言うと、これを実証するのは大変難しい。なぜなら、苦しい筋トレを自ら進んで行うような人はそもそも向上心が強い可能性があるので、そのような人はおそらく社会的に成功する可能性も高いだろうからだ。図で整理すると以下のようになる。

f:id:mstour:20200912074249j:plain — 筋トレ、向上心、社会的成功の関係性の模式図

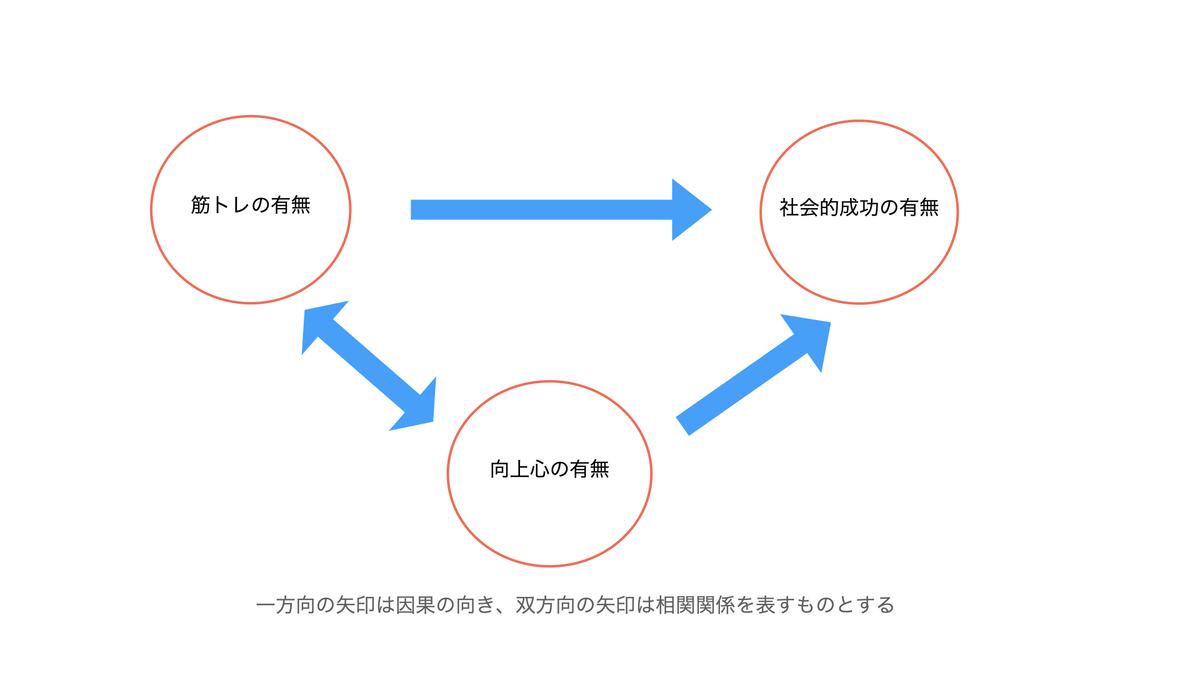
もう少し詳しく述べると、観察結果だけに基づくと「筋トレをすれば社会的に成功する」傾向にあるかもしれないが、「向上心のある人が社会的に成功する」可能性は高く（一方向の矢印で表現）、かつ「筋トレをするかどうかと向上心の高さとには相関関係がある」可能性も高い（双方向の矢印で表現）。したがって、単に向上心の高い人は社会的に成功しやすいという当たり前のことが、筋トレという現象を通して表面に出ているだけかもしれない。
このようなとき、「交絡」と呼ばれる現象が生じてしまい、本当は筋トレと社会的成功になんの関係もないにもかかわらず、向上心の影響で見せかけの関連性が現れることがある。向上心の影響を取り除いて評価するためには基本的に2つの方法しかなく、1つはランダム化比較試験（つまり被験者を筋トレをするグループとしないグループにランダムに分ける）、もう1つは層別解析などによる調整である。
とっても前置きが長くなったが、このときにMH検定が効果を発揮することになる。では具体的に何をするかというと、例えば向上心が「向上心あり」「向上心なし」という2つにうまく分けられるような場合、向上心ありのグループと向上心なしのグループそれぞれで筋トレと社会的成功との関連性を計算し、最後にその結果を統合するということを行う。こうすることで、向上心の影響を取り除いた評価が可能になる。向上心あり・なしの両方のグループで筋トレが社会的成功に影響するという結果が出れば、確かに筋トレが影響しているんだなということが言えそうである。
（なお、筆者は筋トレの社会的成功への影響を否定している訳ではなく、むしろその可能性は高いと個人的に思っている）

数学的定義

今回は話を単純にするために $2 \times 2$ 分割表で表される場合だけを扱うことにする。
まず、層が1つ（層別しない）の場合を考える。分割表は以下のようになる。なお、結果変数は「反応あり」「反応なし」の2つの値をとるものとする。

	群1	群2	合計
反応あり	$a$	$b$	$m_1$
反応なし	$c$	$d$	$m_2$
合計	$n_1$	$n_2$	N

通常、研究計画によって群1と群2（例えば、実薬を投与するグループと偽薬（プラセボ）を投与するグループ）の人数（列方向の合計）は固定されており、群1の反応ありの人数、群2の反応ありの人数はそれぞれ試行数 $n_1$ と $n_2$ の二項分布に従うものと考えて統計的評価を行う。しかし、MH検定では行方向の合計、つまり反応ありの合計人数 $m_1$ と反応なしの合計人数 $m_2$ も固定しての評価を行う。行・列両方の合計を固定する時、群1の反応確率を $\pi_1$ 、群2の反応確率を $\pi_2$ とすると、群1の反応ありの人数 $a$ はオッズ比

$\displaystyle \varphi = \frac{\pi_1 / (1-\pi_1)}{\pi_2 / (1-\pi_2)}$

を非心パラメータとする超幾何分布に従う。
さて、群1と群2とで反応確率が等しいか否か、言い換えるとオッズ比 $\varphi$ が1か否かを確かめたいことが多い。オッズ比が1という帰無仮説のもとでは、群1の反応ありの人数 $a$ は中心超幾何分布に従うことが知られている（以下、単に「超幾何分布」とする）。この時、 $a$ の期待値と分散は

$\displaystyle E(a) = \frac{n_1 m_1}{N} \\ V(a) = \frac{n_1 n_2 m_1 m_2}{N^2 (N-1)}$

となり、 $Z$ 統計量

$\displaystyle Z = \frac{a - E(a)}{\sqrt{V(a)}}$

は漸近的に標準正規分布に従う。これを二乗した

$\displaystyle \chi^2_{MH} = Z^2 = \frac{\left( a - E(a) \right)^2}{V(a)}$

がMH検定統計量と呼ばれるものであり、自由度1のカイ二乗分布に漸近的に従う。
層別解析を行う場合にも同様の検定統計量を用いることになる。いま、層の数を全部で $K$ 個とする。 $k$ 番目の層における分割表は以下のように表される。

	群1	群2	合計
反応あり	$a_k$	$b_k$	$m_{1k}$
反応なし	$c_k$	$d_k$	$m_{2k}$
合計	$n_{1k}$	$n_{2k}$	N_k

MH検定によって層別解析を行う場合、オッズ比（同様だが、群1と群2の反応確率）はすべての層で共通であるとの仮定を置く。ただし、この仮定が満たされない（つまり、群の効果と層別に用いる変数との間に交互作用がある）からといって層別解析の妥当性に問題があるわけではないとされるが（例えばフライス(2004)参照）、検出力は下がることになる。
MH検定では、帰無仮説を「各層の共通オッズ比は1である（=どの層でも群1と群2の反応確率は同じ）」、対立仮説を「各層の共通オッズ比は1でない（=どの層でも群1と群2の反応確率が同じだけ異なる）」とする。帰無仮説が正しいとするとき、各層のセル度数 $a_k$ の期待値と分散は

$\displaystyle E(a_k) := E_k = \frac{n_{1k} m_{1k}}{N_k} \\ V(a_k) := V_k = \frac{m_{1k} m_{2k} n_{1k} n_{2k}}{N_k^2 (N_k - 1)}$

であり、 $a_k - E_k$ は漸近的に正規分布 $N(0, V_k)$ に従う。各層の独立性より、各層にわたる総和 $\sum_{k=1}^{K}(a_k - E_k)$ は漸近的に正規分布 $N(0, \sum_{k=1}^{K})$ に従うので、総和 $\sum_{k=1}^{K}(a_k - E_k)$ の2乗を分散で割った以下のカイ二乗統計量

$\displaystyle \begin{eqnarray} \chi^2_{MH} &=& \frac{\left[ \sum_{k=1}^{K} (a_k - E_k) \right]^2}{\sum_{k=1}^{K} V_k} \\ &=& \frac{ \left[ \sum_{k=1}^{K} (a_k - n_{1k} m_{1k} / N_k ) \right]^2 }{\sum_{k=1}^{K} \left( \frac{m_{1k} m_{2k} n_{1k} n_{2k}}{N_k^2 (N_k-1)} \right)} \end{eqnarray}$

が漸近的に自由度1のカイ二乗分布に従うことを用いて仮説の検定を行うことになる。
つまり、検定統計量 $\chi^2_{MH}$ の値が大きくなればなるほど、帰無仮説が正しいという想定では起こりにくいようなデータが得られていることになるので、各層の共通オッズ比は1である（=どの層でも群1と群2の反応確率は同じ）という仮説は間違っているだろうと判断することになる。
MH検定は $2 \times 2$ 分割表の場合だけでなく、複数カテゴリーの変数や順序カテゴリー変数にも用いることができるが、それはまた別の機会に書いてみたい。

まとめ

今回はMantel-Haenszel検定（MH検定）の意義について、交絡の話をまじえて述べた。また数学的定義を紹介した。層ごとに分割表の計算を行って最後に結果を結合するという、直感的にわかりやすい方法であるが、MH検定のような層別による方法ではカテゴリー型の変数しか交絡の調整をすることができないのが難点である。連続型の変数を調整したい場合はある値で区切ってカテゴリー化すれば層別できるが、素直に回帰モデル（結果変数が2値の場合にはロジスティック回帰）を用いるのがよいだろう。

参考文献

[1] John M. Lachin(2020), "医薬データのための統計解析", 共立出版.
[2] Busing, F.M.T.A. et al.(2016), "2 × 2 Tables: a note on Campbell’s recommendation", Statist. Med.,35 1354–1358.
[3] J.L.フライス(2004), "臨床試験のデザインと解析", アーム.