しばらくお休みします

といっても、もう長いこと書いていないのですが・・・
新しい記事を書く時間の余裕・エネルギーの余裕がなくなってしまったので、当分の間お休みします。

ありがたいことに、複数の方からこのブログの記事の内容を参考にしたとおっしゃっていただいて、本当に嬉しく思いました。
声を掛けてくださった方には、この先、何らかの形でお返しができたらと思います。

また気が向いたら何か書きます。

傾向スコアを用いたOverlap weighting

はじめに

傾向スコアを用いた解析の代表的な方法の一つとして、個人ごとの傾向スコアの推定値*1による重み付け解析があります。

重み付け解析としては、傾向スコア推定値の逆数で重み付けを行う「逆確率重み付け法(Inverse probability of treatment weighting; IPTW)」が有名で広く利用されていますが、この方法は傾向スコアの推定値に0または1に近いものがあった場合（つまり、重みが非常に大きくなる場合）に、推定のバラツキが大きくなってしまうという難点があります。そのため、例えば極端な重みの値を持つ個人を解析から除外する「トリミング(Trimming)」などの方策がこれまでにも提案されてきました。

一方で最近では、新しいタイプの重み付け手法である「Overlap weighting」が提案されています。この方法については、Liらの2018年の論文（参考資料[1]）をはじめいくつか詳しく論じた文献があります。

Overlap weightingには、

• 重みが必ず0から1の間の値になる
• 傾向スコアによる重み付け解析の中では、最も推定精度が高い*2
• ロジスティック回帰で傾向スコアを推定した場合、背景因子の平均が処置グループ間で完全に一致する（平均の差がゼロになる）

といった理論的に優れた特徴があり、また

• いずれの処置を受ける可能性も同程度あるような集団に対する処置効果を推定する

という実際的な特徴も持っています。

今回は、Overlap weightingの概要と、Rでの解析例を紹介したいと思います。

Overlap weightingとは

傾向スコアによるIPTW

一般に重み付け解析では、各個人のデータに、対応する重みを掛け算したものをその個人のデータとみなして解析を行う形になります。
個人の重みをとすると、例えば変数の重み付け平均は

により計算されます。なお分母は重みの合計です。
重みは各個人のデータがそれぞれ何人分の価値があるのかを表している、と考えると理解しやすいと思います。

処置群と対照群の平均の差を考える場合には、次のように表現することが多くあります。

ここでは個人が処置群に所属している場合1を、対照群に所属している場合0をとる変数です。
したがっては処置群の人数、は対照群の人数を意味しており、上記は処置群の重み付け平均と対照群の重み付け平均の差を表していることになります。

さて、傾向スコアによる重み付け解析のうち、IPTWは「逆確率重み付け法」の名前の通り、「割り当てられた処置を受ける確率の逆数で重み付けする」方法でした。
つまり、IPTWで使用する重みは推定された傾向スコア（=処置を受ける確率。は処置を受けない確率）の逆数で、処置群の場合、対照群の場合となります。

上記の定義をよく見るとわかるように、傾向スコアが0に近い（=本来なら処置を受けなさそうな）個人が処置群に所属する場合・あるいは1に近い（=本来なら処置を受けそうな）個人が対照群に所属する場合には、重みが非常に大きな値になってしまいます。
これらの状況では、処置効果の推定にバイアスが入ったり、推定のバラツキ（分散）が大きくなるなどの問題が生じることが知られています。

Overlap weighting

一方で、近年提案されたのがOverlap weightingと呼ばれる重み付け解析方法です。
Overlap weightingに用いる重み（Overlap weightと呼びます）は、自分が属していない群に属する確率（つまり、処置群に所属する個人であれば、対照群に属する確率）として定義されます。この重みは推定した傾向スコアで表すことができ、処置群の場合、対照群の場合となります。

Overlap weightingには、傾向スコアの値が0.5に近い個人が処置効果の推定に最も影響を与える一方、0あるいは1に近づくにつれて影響度が小さくなるという特徴があります。
具体的に、単純なケースで考えてみましょう。

処置群、対照群それぞれに150人ずつがいるものとし、下記の表の「傾向スコア」の列には各個人のもつ傾向スコアの値、「人数(%)」の列はその傾向スコアの値をもつ個人の人数および構成割合(%)を示しています。また、「IPTW後の人数(%)」「OW後の人数(%)」はそれぞれIPTW、Overlap weighting(OW)を行った後の（仮想的な）人数および構成割合です。

＜処置群＞

傾向スコア	人数(%)	IPTW後の人数(%)	OW後の人数(%)
0.5	50(33.3%)	250=100(33.3%)	0.550=25(43.9%)
0.2	20(13.3%)	520=100(33.3%)	0.820=16(28.1%)
0.8	80(53.3%)	1.2580=100(33.3%)	0.280=16(28.1%)

＜対照群＞

傾向スコア	人数	IPTW後の人数(%)	OW後の人数(%)
0.5	50(33.3%)	250=100(33.3%)	0.550=25(43.9%)
0.2	80(53.3%)	1.2580=100(33.3%)	0.280=16(28.1%)
0.8	20(13.3%)	520=100(33.3%)	0.820=16(28.1%)

この例では、IPTWを行うと、どの傾向スコアの値をもつ個人も各群における構成割合は33.3%となり、処置効果の推定に等しく影響することになります。
一方でOWでは傾向スコアの値が0.5の個人の構成割合が半数近くになっており、逆に傾向スコアの値が0あるいは1に近づくほど構成割合が小さくなっているのがわかります。したがって、OWでは、傾向スコアが0.5に近い個人ほど処置効果の推定に強く影響することになります。

（上記の数値例を再現するRコード例です。）

library(tidyverse)
library(WeightIt)

x <- c(rep("A", 50), rep("B", 20), rep("C", 80), rep("A", 50), rep("B", 80), rep("C", 20))
trt <- c(rep("T", 150), rep("C", 150))
toy_df <- tibble(covariate = x, treat = trt)

toy_ps <- weightit(trt ~ covariate, data = toy_df, method = "ps", estimand = "ATE")
toy_df_weight <- toy_df %>%
  mutate(ps = toy_ps$ps,
         iptw_wgt = case_when(treat == "T" ~ 1/ps, treat == "C" ~ 1/(1-ps)),
         ovlp_wgt = case_when(treat == "T" ~ 1-ps, treat == "C" ~ ps))

toy_df_weight %>% group_by(treat, ps) %>%
  summarise(iptw_size = sum(iptw_wgt), ovlp_size = sum(ovlp_wgt))

このようにOverlap weightingは傾向スコアが0.5に近い（背景因子が処置群間でオーバーラップするような）集団に重点を置くため、重み付け解析によって得られる処置効果の推定値は処置群・対照群をあわせた全体集団に対するもの（平均処置効果(Average treatment effect; ATE)）ではなくなります。
Overlap weightingを用いて推定した処置効果のことは、文献によってはAverage treatment effect for the overlap population(ATO)と呼ばれています。

ATOは傾向スコアが0.5に近い個人に大きな重みが置かれているため、異なる処置Aと処置Bのどちらを受ける可能性も同じくらいあるような集団での効果を見ているものと解釈できます。
例えば、軽症の患者には治療Aが、重症の患者には治療Bが標準治療とされているが、中程度の症状の患者にはどちらの治療をすればよいか分かっていないため両方の治療が選択されうる、という状況を考えてみます。
このような場合、重症度を用いて治療Aに対する傾向スコアを推定すると*3、軽症患者は1に近い値、中程度の患者は0.5に近い値、重症患者は0に近い値が得られるでしょう。そこでOverlap weightingを行うと、中程度の患者を中心とした集団での処置効果（治療Aと治療Bとの差）を推定できるはずです。

臨床研究の文脈における解説として、例えばThomasらのJAMAの記事（参考文献[2]）が参考になります。

Overlap weightingは元々は統計の理論的な面から研究がなされており、様々な重み付け解析の中で処置効果の推定量の漸近分散が最小になることが示されています。
またロジスティック回帰で傾向スコアを推定した場合に、Overlap weighting後の背景因子の平均がグループ間で一致するという性質もあります（後述する例もご覧ください）。
純粋に統計的な観点からよい性質をもつだけでなく、重み付け解析で推定した処置効果を明快に解釈できるため、理論・応用の両面から今後利用が広がっていくものと思われます。

Rによる解析例

Overlap weightingは、前回の記事で紹介したRのPSweightパッケージで行うことができます。
mstour.hatenablog.com

前回と同じく、twangパッケージに付属しているデータセットである"lindner"を用いて解析例を紹介していきます。
lindnerデータセットの説明については、前回の記事やtwangパッケージの解説などをご参照ください。

まずはPSweightとtwangを読み込み、lindnerデータセットも準備します。

library(PSweight)
library(twang)

data("lindner", package = "twang")

PSweightパッケージを用いた重み付け解析の流れは、前回紹介したものと同様です。
まず傾向スコアのモデル式を定義します。

# PSのモデル式
psmodel_ovlp <- abcix ~ stent + height + female + diabetic + acutemi + ejecfrac + ves1proc

ここで、重み付けをした場合の背景因子のバランスがどうなるかを確認しておきます。
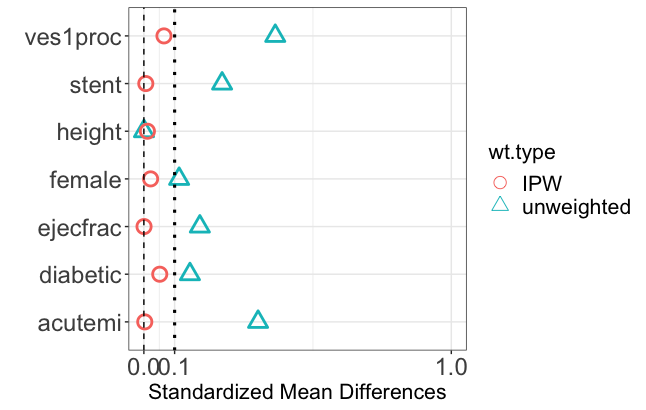
最初にSumStat関数でweight = "overlap"と指定することでoverlap weightの計算を行い、続いてplot関数でtype = "balance"を指定することで、Overlap weightingを行った際の背景因子の標準化差(Standardized mean difference)を確認できます。

# weighting後のバランス
bal_ovlp <- SumStat(ps.formula = psmodel_ovlp, data = lindner, weight = "overlap")
plot(bal_ovlp, type = "balance")

IPTWを行った場合との違いを見てみましょう。上の図の赤丸がIPTW、下の図の赤丸がOverlap weightingでの標準化差です。

IPTWを行った場合の背景因子の標準化差

Overlap weightingを行った場合の背景因子の標準化差

このデータにおいては、IPTWを行うことで背景因子の標準化差はすべて0.1未満になり、治療グループ間でおおむねバランスがとれているといえます。
ところが、Overlap weightingを行った場合には、背景因子の標準化差は完全に0になっています。これは理論的に示されているOverlap weightingの一つの特徴であり、交絡によるバイアスを取り除いたり推定精度を上げるために有効であると考えられます。

一方で前述の通り、IPTWとOverlap weightingとでは、一般に処置効果の推定の対象となる集団が異なってくることに注意が必要です。
調整に用いた背景因子について、Overlap weightingとIPTWそれぞれによる重み付け後の要約統計量を見てみると、今回のデータでも若干の差異があることがわかるかと思います。例えばacutemi（急性心筋梗塞）の割合はOverlap weightingではIPTWの場合の半分ほどになっています。
なおPSweightなどのパッケージ単体では簡単に背景集計ができないようでしたので、今回は重みを算出し直した上で、gtsummaryパッケージの"tbl_svysummary"という重み付け集計の関数を使用して計算しました（参考資料[6]）。

# 傾向スコアの算出
psmodel_man <- glm(abcix ~ stent + height + female + diabetic + acutemi + ejecfrac + ves1proc,
                   data = lindner, family = binomial)
ps_man <- psmodel_man$fitted.values

# overlap weightと逆確率重みをデータセットに格納
wgt_man <- lindner %>%
  mutate(ps = ps_man,
         ovlp_wgt = case_when(abcix == 1 ~ (1-ps_man), abcix == 0 ~ ps_man),
         iptw_wgt = case_when(abcix == 1 ~ 1/ps_man, abcix == 0 ~ 1/(1-ps_man))
  )

# surveyパッケージで重み付けした後、gtsummaryパッケージで集計
library(gtsummary)
library(survey)

## Overlap weighting
tbl_ovlp <- svydesign(~1, data = wgt_man, weights = wgt_man$ovlp_wgt) %>%
  tbl_svysummary(include = c(stent, height, female, diabetic, acutemi, ejecfrac, ves1proc),
                 type = list(stent ~ "dichotomous",
                             height ~ "continuous",
                             female ~ "dichotomous",
                             diabetic ~ "dichotomous",
                             acutemi ~ "dichotomous",
                             ejecfrac ~ "continuous",
                             ves1proc ~ "continuous"),
                 by = abcix,
                 statistic = list(all_continuous() ~ "{mean}({sd})"),
                 digits = list(all_continuous() ~ c(1, 2), all_categorical() ~ c(0, 1))) %>%
  modify_header(label = "**After Overlap weighting**")
tbl_ovlp

## IPTW
tbl_iptw <- svydesign(~1, data = wgt_man, weights = wgt_man$iptw_wgt) %>%
  tbl_svysummary(include = c(stent, height, female, diabetic, acutemi, ejecfrac, ves1proc),
                 type = list(stent ~ "dichotomous",
                             height ~ "continuous",
                             female ~ "dichotomous",
                             diabetic ~ "dichotomous",
                             acutemi ~ "dichotomous",
                             ejecfrac ~ "continuous",
                             ves1proc ~ "continuous"),
                 by = abcix,
                 statistic = list(all_continuous() ~ "{mean}({sd})"),
                 digits = list(all_continuous() ~ c(1, 2), all_categorical() ~ c(0, 1))) %>%
  modify_header(label = "**After IPTW**")
tbl_iptw

Overlap weighting後の背景因子の要約統計量

IPTW後の背景因子の要約統計量

では、Overlap weightingにより処置効果を推定します。
推定計算は"PSweight"関数で行い、結果を"summary"関数で表示します。二値アウトカムの場合、type = "DIF"を指定すると割合の差（リスク差）が出力されます。
割合の比（リスク比）やオッズ比を算出したい場合はそれぞれtype = "RR"、type = "OR"と指定します。

est_ovlp <- PSweight(ps.formula = psmodel_ovlp, yname = "sixMonthSurvive", data = lindner,
                     weight = "overlap")
summary(est_ovlp, type = "DIF")

以下の出力のように、6ヶ月後の生存割合の差は4.01%(95%信頼区間は1.12 - 6.78%)という結果でした。

Overlap weightingによる生存割合の差の推定結果

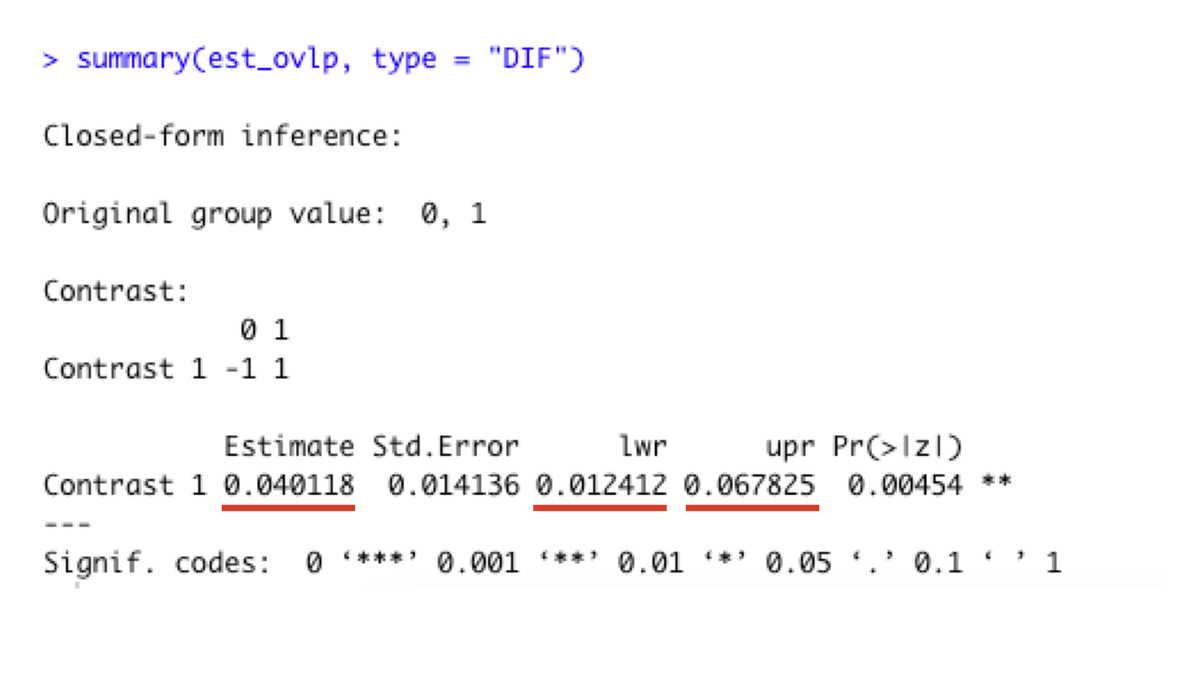
なおIPTWによる推定値は6.61%(95%信頼区間は1.21 - 12.0%)になりました。
あくまで例示用の模擬データではありますが、

• 推定対象となる集団が異なるために、処置効果（生存割合の差）はOverlap weightingとIPTWとで異なる結果になった
• Overlap weightingのほうがIPTWよりも背景因子を強力にバランスさせてくれた結果、バラツキが小さくなり、信頼区間の幅が狭くなった

といえるのではないかと思います。

まとめ

今回は傾向スコアによる重み付け法のひとつであるOverlap weightingを紹介しました。

最もポピュラーな重み付け法であるIPTWは、集団全体における処置効果を推定することのできる強力な方法ですが、傾向スコアに極端な値が存在する場合には推定にバイアスが入る危険があるのが難点です。

Overlap weightingでは、重みは必ず0〜1の間の値をとるため、IPTWのように極端な重みに引きずられることがありません。また今回詳しくは述べませんでしたが、背景因子のバランスや推定精度の面で優れた性質を持っています。
うまく使いこなすことができればとても魅力的な方法だと思います。

Overlap weightingの方法論に関する参考文献はこちら。

[1] Li, F., Morgan, K. L., & Zaslavsky, A. M. (2018). Balancing covariates via propensity score weighting. Journal of the American Statistical Association, 113(521), 390-400.
[2] Thomas, L. E., Li, F., & Pencina, M. J. (2020). Overlap weighting: a propensity score method that mimics attributes of a randomized clinical trial. Jama, 323(23), 2417-2418.
[3] Li, F., Thomas, L. E., & Li, F. (2019). Addressing extreme propensity scores via the overlap weights. American journal of epidemiology, 188(1), 250-257.

Rでの実行に関する参考文献はこちら。

[4] Propensity Score Weighting in R: A Vignette.
https://cran.r-project.org/web/packages/PSweight/vignettes/vignette.pdf
[5] Ridgeway, G., McCaffrey, D., Morral, A., Cefalu, M., Burgette, L., Pane, J., & Griffin, B. A. (2021). Toolkit for Weighting and Analysis of Nonequivalent Groups: A guide to the twang package. vignette, July, 26.
[6] Create a table of summary statistics from a survey object — tbl_svysummary • gtsummary

*1:本記事ではイメージしやすいよう解析の単位を「個人」と表記することにしました。

*2:正確には、サンプルサイズが大きい時の漸近的な分散が最小になることが示されています。

*3:本来傾向スコアを用いるのは他にもたくさんの調整すべき因子がある場合ですが、ここでは話を単純にするために重症度だけを考えました。

傾向スコア法による重み付け解析を行うためのRパッケージいくつか

はじめに

前回の記事では、傾向スコア(Propensity score)による逆確率重み付け法(Inverse probability of treatment weighting; IPTW)をRで行うためにIPWパッケージを用いました。

実は、傾向スコア法による解析を行うためのRのパッケージはたくさんあり、僕自身どれを使えばいいのかいまいちよくわかっていません。
例えば、後述するPSweightパッケージのチュートリアルペーパーでは、重み付けを行えるパッケージだけでも少なくとも9つがあることが述べられています。

そこで今回は、その中で比較的目にすることの多いパッケージ3つを紹介し、サンプルデータを使って基本的な解析の手順を書いていきたいと思います。
なお今回はIPTWの場合に限定しますが、それぞれのパッケージは他の重み付け（例えば、処置群における処置効果(Average treatment effect on the treated; ATT)の推定）にも対応しています。

今回紹介するのは以下のパッケージです。

• WeightIt
• twang
• PSweight

今回紹介するRパッケージ。コメントは個人的な感想です。

実行例

まずは、今回使用するパッケージを読み込んでおきます。

library(tidyverse)
library(broom)

library(WeightIt)
library(twang)
library(PSweight)

library(cobalt)

library(survey)

• tidyverseは、データの加工やプロットに必須のパッケージです。
• broomはtidyverseに含まれるパッケージですが、別途読み込むことで統計モデルの出力結果をデータフレーム形式（正確にはtibble形式ですが、以降ではデータフレームと呼ぶことにします）に変換するtidy関数が使用できます。
• WeightIt、twang、PSweightは、今回のIPTWの解析に使用する3パッケージです。
• cobaltは傾向スコアによる調整の前と後の共変量のバランスを確認するのに便利なパッケージです。
• surveyは、IPTWにおいて、処置効果の推定量の標準誤差にロバスト分散(Robust variance)を適用するために用います。*1

サンプルデータの説明と未調整の解析

今回は、twangパッケージに付属しているサンプルデータセットの"lindner"を使用します。

data("lindner", package = "twang")

データセットの最初の10行は以下のようになっています。

lindnerデータセット。

このlindnerデータセットには、経皮的冠動脈インターベンション（PCI）を受けた996名の治療後6ヶ月後の生存状況が記録されています。
また処置変数はアブシキシマブという薬剤の投与有無であり、PCIに加えてこの薬剤を投与することにより、6ヶ月後の生存状況に違いがあるのかを評価したいものとします（参考資料[2]・twangパッケージのチュートリアルペーパーや、参考資料[3]のウェブサイト The Lindner Example を参照）。
今回の解析例では以下の変数を使用します。

• abcix：アブシキシマブ投与の有無（1：あり、0：なし）
• stent：ステント挿入の有無（1：あり、0：なし）
• height：身長（cm）
• female：性別（1：女性、0：男性）
• diabetic：糖尿病の有無（1：あり、0：なし）
• acutemi：最近の急性心筋梗塞の有無（1：あり、0：なし）
• ejecfrac：左室駆出率（%）
• ves1proc：PCIの対象になった血管の数
• sixMonthSurvive：PCI6ヶ月後の生存状況（TRUE：生存、FALSE：死亡）

以下、アブシキシマブ投与ありのグループを処置群、投与なしのグループを対照群とよぶことにします。またPCI6ヶ月後の生存割合をアウトカムとし、処置効果は生存割合の差で評価するものとします。

まずは、共変量の調整なしで処置効果を算出してみます。
今回は生存割合の差*2について、正規分布による近似を考え、線形回帰モデルにより算出しました。

# 共変量調整をしない解析
mod_naive <- glm(sixMonthSurvive ~ abcix, data = lindner, family = gaussian)

## tidy(conf.int = TRUE)により推定値と信頼区間をデータフレーム化
mod_naive %>% tidy(conf.int = TRUE)

abcixの行に、生存割合の差や信頼区間が表示されています。生存割合の差は3.46%（95%CI : 1.30-5.61%）ほどのようです。

背景を調整しない解析の結果

しかし、次に見るように両グループの背景因子には偏りが生じており、処置の効果を正しく推定するためには背景因子の調整を行う必要がありそうです。*3
そこで、背景因子の分布について、cobaltパッケージを用いて確認してみます。

cobaltパッケージには、グループ間の背景因子のバランスを数値化して出力するbal.tab関数や、背景因子の偏りの度合いを表す標準化差(Standardized mean difference)を視覚的に表現してくれるlove.plot関数などが搭載されています。
ここではlove.plotを使用してみましょう。

love.plot(abcix ~ stent + height + female + diabetic + acutemi + ejecfrac + ves1proc,
                  data = lindner, estimand = "ATE",
                  abs = TRUE, stats = "mean.diffs", thresholds = c(m = 0.1),
                  s.d.denom = "pooled", binary = "std")

以下の図が出力されます。

縦軸には背景因子、横軸にはそれらの因子の「標準化平均差(Standardized mean difference)」（グループ間の平均値の差を、標準偏差で割って標準化したもの）の絶対値が表示されています*4。この標準化平均差の絶対値は0.1未満になることが好ましいとされていますが、stent、acutemi、ves1procについてグループ間で比較的大きな偏りがあるように見えます。
なお、以降では標準化平均差をSMDと表記します*5。

WeightItパッケージ

では、傾向スコアによるIPTWで解析してみましょう。
まずはWeightItパッケージを使用します。これは傾向スコアの重み付け解析に特化したパッケージで、使われている方も多いかと思います。なお傾向スコアマッチングについてはMatchItというパッケージがあります。

傾向スコアモデルから重みを算出するには、weightit関数を使用します。
まずglm関数などと同様の記法によって傾向スコアのモデル式を定義します。またmethod = "ps"とすることで、ロジスティック回帰によって傾向スコアが推定されます。傾向スコアの推定方法は他にも"generalized boosted modeling"のような機械学習の手法も選択できます。
estimand = "ATE"とすることにより、IPTWに用いる逆確率重みが計算されます。他には"ATT"などの選択肢があります。

# 傾向スコアの推定と重みの算出
psmodel_wtit <- weightit(abcix ~ stent + height + female + diabetic + acutemi + ejecfrac + ves1proc,
                              data = lindner, method = "ps", estimand = "ATE")

上記で得られた結果から、$psで傾向スコアの推定値を、$weightsで重みを取り出すことができます。

# 傾向スコアと重みをもとのデータセットに格納
lindner_iptw_wtit <- lindner %>%
  mutate(ps = psmodel_wtit$ps, weight = psmodel_wtit$weights)

推定した傾向スコアの両グループでの分布を、cobaltパッケージのbal.plot関数で確認してみましょう。

# propensity scoreの分布
bal.plot(lindner_iptw_wtit, treat = lindner_iptw_wtit$abcix, var.name = "ps")

傾向スコアの分布に重なり合う部分が少ない場合には解析が不適切になる恐れがありますが、今回は大きな偏りはなさそうですので、このまま解析を進めても大丈夫ということにします。

重み付け後の背景因子のバランスも確認してみましょう。

love.plot(abcix ~ stent + height + female + diabetic + acutemi + ejecfrac + ves1proc,
          data = lindner_iptw_wtit, weights = lindner_iptw_wtit$weight,
          abs = TRUE, stats = "mean.diffs", thresholds = c(m = 0.1),
          s.d.denom = "pooled", binary = "std")

赤色の点が調整前のSMD絶対値、青色の点が傾向スコアによるIPTWを行った後でのSMD絶対値です。
重み付けを行うことにより、背景因子のバランスが非常に改善されているのが分かります。

続いてIPTWにより生存割合の差を推定するため、surveyパッケージのsvyglm関数によって重み付け解析を行います。解析モデルは調整なしの場合と同様に線形回帰としました。

# 重みやデータの情報を格納
design_wtit <- svydesign(id = ~ 1, weights = ~ weight, data = lindner_iptw_wtit)

# 重み付けの線形回帰
mod_iptw_wtit <- svyglm(sixMonthSurvive ~ abcix,
                      design = design_wtit, family = gaussian())

# 割合の差の推定値を出力
mod_iptw_wtit %>% tidy(conf.int = TRUE)

結果は以下の通りです。生存割合の差は6.61%（95%CI : 0.80 - 12.40%）で、調整しない場合と比べ差が大きくなりました。もともとの背景因子の偏りを考えると、推定にバイアスを生じさせるような交絡がIPTWによって取り除かれた可能性があります*6。

WeightItパッケージを用いたIPTWの結果

twangパッケージ

続いて、twangパッケージでの解析例です。
twangパッケージの初期バージョンの開発は2004年であり、かなり歴史のあるパッケージです。元々このパッケージは、ロジスティック回帰を用いて最適な傾向スコアモデルを構成する（交互作用や高次の項も含め、どのような説明変数をモデルに入れるかを決定する）作業が非常に負担になっている状況を改善するために、機械学習の手法を用いて自動的に最適な傾向スコアモデルを決定できるようにしたいというのが開発の動機だったようです（参考資料[4]・RAND Corporationのウェブサイト Toolkit for Weighting and Analysis of Nonequivalent Groups (TWANG) | RAND ）。

twangパッケージでの傾向スコアの推定は機械学習の手法であるgradient boostingによって行われており、Rでの設定についてもそれらの知識が必要になる箇所が見受けられます。
そのため、この記事内では詳細には触れず、IPTWの解析手順のみ紹介します（力不足で申し訳ありません）。
またチュートリアル（参考資料[2]）の例にもあるように、twangによる解析結果はロジスティック回帰により傾向スコアを推定した場合と異なることがあるようです。これは傾向スコア推定方法の違いによるものと考えられます。
古典的なロジスティック回帰とブースティングなどの機械学習手法のどちらを用いるのがよいかは、ここでは一概には言えない難しい問題のように思います。

さて、まずは傾向スコアを推定して、重みを取得します。

# 傾向スコアの推定
psmodel_twng <- ps(abcix ~ stent + height + female + diabetic + acutemi + ejecfrac + ves1proc,
                   data = lindner, estimand = "ATE", verbose = FALSE)

# 重みをget.weights関数で取得
lindner_iptw_twng <- lindner %>%
  mutate(weight = get.weights(psmodel_twng, stop.method = "es.mean"))

WeightItと異なり、twangパッケージには傾向スコアや背景因子のバランスを確認するための関数があらかじめ用意されています（ただしcobaltと体裁は異なります）。前述と同様の図を作成するには、以下のコードを実行します。

# propensity scoreの分布
plot(psmodel_twng, plots = 2)

# weighting後のバランス
plot(psmodel_twng, plots = 3)

重み付け解析については、WeightItの時と同様にsurveyパッケージの関数などを利用する必要があるようです。

# 調整解析
design_twng <- svydesign(id = ~ 1, weights = ~ weight, data = lindner_iptw_twng)
mod_iptw_twng <- svyglm(sixMonthSurvive ~ abcix,
                        design = design_twng, family = gaussian())

mod_iptw_twng %>% tidy(conf.int = TRUE)

結果は以下の通りで、WeightItパッケージで解析した場合と異なり、調整をしない場合とほとんど変わらない推定値になりました。
twangで推定した傾向スコアでは背景因子のバランスが揃えきれていないためか、逆にWeightItでの傾向スコアモデルが妥当でなく（ロジスティックモデルが適切でない、共変量の交互作用などが必要、など）そちらの解析結果が間違っているのかはこれだけでは判断がつきませんが、このようなことが起こりうると考えておいたほうがよさそうです。

twangパッケージを用いたIPTWの結果

PSweightパッケージ

PSweightパッケージは、2020年に登場した比較的新しいパッケージです。
これも傾向スコアによる重み付け解析に特化したパッケージですが、WeightItやtwangと大きく異なるのは、傾向スコア推定と重みの算出、バランス確認、重み付け解析をすべて一つのパッケージの中で完結できる点です。また、最近注目されている重み付け方法であるOverlap weightingにも対応しています*7。

ここではチュートリアルペーパー（参考資料[5] https://cran.r-project.org/web/packages/PSweight/vignettes/vignette.pdf）に沿って、PSweightの使用例を紹介します。
まず最初に、傾向スコアモデルの数式をオブジェクトへ格納します。
数式の表記法はglm関数などと同様のおなじみのものです。

# PSのモデル式
psmodel_pswt <- abcix ~ stent + height + female + diabetic + acutemi + ejecfrac + ves1proc

傾向スコアの分布や重み付け後の背景因子のバランスを確認するには、SumStat関数により傾向スコアの推定を行い、その結果にplot関数を適用します。weight = "IPW"を選択することで逆確率重み付け法(IPTW)の重みが得られますが、他にもoverlap weight（weight = "overlap"）やATTを推定するための重み（weight = "treated"）などが選択できます。

# 傾向スコアや重みの情報を取得
bal_pswt <- SumStat(ps.formula = psmodel_pswt, data = lindner, weight = "IPW")

# 傾向スコアの密度
plot(bal_pswt, type = "density")

# 背景因子のバランス
plot(bal_pswt, type = "balance")

傾向スコアの分布と背景因子のバランスについて、それぞれ以下のようなプロットが出力されます。

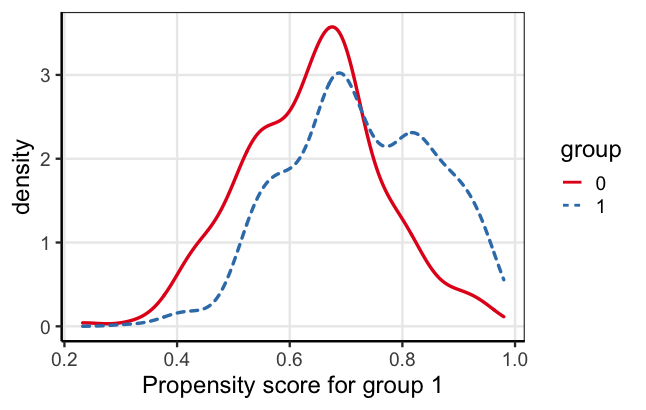
PSweightもロジスティック回帰により傾向スコアを推定しているので、WeightItの場合と同じ結果になっているのが分かるかと思います。

最後にIPTWによる生存割合の差の推定を行います。PSweight関数で推定を行い、summary関数で推定結果を表示します。
なおsummary関数のデフォルトではグループ間の平均の差（二値アウトカムの場合、割合の差）が出力されますが、二値アウトカムの場合にはtype = "RR"と指定するとリスク比が、type = "OR"と指定するとオッズ比が出力されます。

# IPTW
ate_pswt <- PSweight(ps.formula = psmodel_pswt, yname = "sixMonthSurvive", data = lindner,
                     weight = "IPW")

# 結果の出力（tidy関数には対応していないようです）
summary(ate_pswt, type = "DIF")

結果は以下のようになりました。
推定値はWeightItと丸め誤差を除き一致しました。標準誤差の算出にはロバスト分散が用いられていますが、surveyとは算出方法が異なっていると思われ、若干異なった結果になりました。

PSweightパッケージを用いたIPTWの結果

おまけ：自力で傾向スコアを計算

最後に、多少の手間はかかりますが、自前でロジスティック回帰を用いてIPTWを行う例を紹介します。
バランスの確認や重み付け解析はWeightItパッケージを用いる場合と同様です。

# 傾向スコアの推定
psmodel_man <- glm(abcix ~ stent + height + female + diabetic + acutemi + ejecfrac + ves1proc,
                   data = lindner, family = binomial)
## 傾向スコア推定値を格納
ps_man <- psmodel_man$fitted.values

# 傾向スコア推定値と逆確率重みをデータフレームへ格納
lindner_iptw_man <- lindner %>%
  mutate(ps = ps_man,
         weight = case_when(abcix == 1 ~ 1/ps, TRUE ~ 1/(1-ps)))

# IPTW
design_man <- svydesign(id = ~ 1, weights = ~ weight, data = lindner_iptw_man)
mod_iptw_man <- svyglm(sixMonthSurvive ~ abcix,
                      design = design_man, family = gaussian())
mod_iptw_man %>% tidy(conf.int = TRUE)

推定結果はWeightItの場合と全く同じになったので省略します。

まとめ

今回は傾向スコアによる重み付け解析を行うためのRパッケージ3つをとりあげ、IPTWを行う例を簡単に紹介しました。

WeightItは王道的なパッケージのような印象で、解説や使用例はweb上に多く見つかるため、使い勝手がよいように思います。
twangは機械学習の手法を用いて傾向スコアの推定を行う点で、他とは少しテイストが異なるパッケージかもしれません。実用上はロジスティック回帰で傾向スコアを推定することが多いように感じますが、ブースティングをはじめとした機械学習の手法を用いた傾向スコア解析の性能についてはさまざまな研究がなされており、有力な選択肢の一つと考えられます。
PSweightは傾向スコアの推定・バランス評価・重み付け解析までを一つのパッケージ内で数行のコードで完結できるのが魅力的に思います。現時点ではグループ間の平均差やリスク差・リスク比・オッズ比の推定にしか対応していないようですが、今後の機能の拡張に期待したいです。

参考資料

[1] Austin, P. C. (2016). Variance estimation when using inverse probability of treatment weighting (IPTW) with survival analysis. Statistics in medicine, 35(30), 5642-5655.
[2] Ridgeway, G., McCaffrey, D., Morral, A., Cefalu, M., Burgette, L., Pane, J., & Griffin, B. A. (2021). Toolkit for Weighting and Analysis of Nonequivalent Groups: A guide to the twang package. vignette, July, 26.
[3] The Lindner Example
[4] Beth Ann Griffin, Greg Ridgeway, Andrew R. Morral, Lane F. Burgette, Craig Martin, Daniel Almirall, Rajeev Ramchand, Lisa H. Jaycox, Daniel F. McCaffrey. Toolkit for Weighting and Analysis of Nonequivalent Groups (TWANG) Website. Santa Monica, CA: RAND Corporation, 2014. http://www.rand.org/statistics/twang.
[5] Propensity Score Weighting in R: A Vignette.
https://cran.r-project.org/web/packages/PSweight/vignettes/vignette.pdf

*1:IPTWでは、統計モデルから標準的な方法で算出した標準誤差は過小評価（その結果、間違って統計的有意になりやすく、また信頼区間は本来あるべき幅よりも狭くなる）になることが知られています。ただしロバスト分散では逆に過大推定となることがあるため、ブートストラップ法による推定を推奨する意見もあります。（参考資料[1]・Austinの論文）

*2:割合の差は「Risk difference; RD」と呼ばれることが多くありますが、生存する割合をリスクと呼ぶと少し不自然なのでその用語は使いませんでした。

*3:背景因子がアウトカムに影響しうるのかの検討はしていませんが、手法の紹介なので、ここではそういうものとして考えてもらえればと思います。

*4:細かな点はlove.plot関数の設定で変更できます。

*5:Absolute standardized mean differenceの頭文字をとるとASMDですが、あまり使われていないように思いますので、絶対値については「SMDの絶対値」と表記することにします。

*6:あくまで手法の例示のため、具体的な解釈には踏み込まないことにします。

*7:Overlap weightingを実行できるパッケージとして他にはPSWパッケージがありますが、現時点では3グループ以上での解析に対応しているのはPSweightパッケージだけのようです。

傾向スコア法はサンプルサイズが小さくても大丈夫なのか：IPTWの例

【最終更新　2022/5/13】

• シミュレーションでのバイアス評価で、推定したい真値を周辺オッズ比とし、モンテカルロ法で算出するようにしました。
• 条件を変えたシミュレーションをfurrrパッケージで行うようにコード例を修正しました。
• その他、細かな表現を改めた箇所があります。

はじめに

観察データを用いて処置の効果を評価したい場合、処置の割り当てがランダムに行われていないことが原因で、単純にアウトカム変数を比較したのでは正しい結果が得られないことがあります。
例えば、セールのお知らせを送る場合と送らない場合とでセール期間中に来店する会員の割合がどれだけ違うかを調べたいとすると、お知らせを送る相手がランダムに決定されていないのであれば、割合の差を単純計算するとミスリーディングな結果を導く可能性があります。

このような場合に有効な解析方法としてよく知られているのが傾向スコア法(Propensity score method)です。*1

ところで、実務上、数十〜数百ほどのサンプルサイズのデータで処置効果の評価をしたい場合がしばしばあります。
ロジスティック回帰などの統計モデルでは、サンプルサイズ（正確にはイベント数）に対する説明変数の数の目安がよく知られており、サンプルサイズが小さい場合には気をつけないといけないことがあります。*2
では、傾向スコア法についてはサンプルサイズがどれくらいあれば大丈夫なのでしょうか？

どれくらいのサンプルサイズなら問題ないのだろう...

この点を調べた研究はそれほど多くないようなのですが、例えば、

Pirracchioらによる報告：
Evaluation of the Propensity score methods for estimating marginal odds ratios in case of small sample size | BMC Medical Research Methodology | Full Text
特にサンプルサイズが小さい場合の、傾向スコアマッチング(Propensity score matching、以下マッチングとします)と逆確率重みづけ(Inverse probability of treatment weighting、以下IPTWとします)の性能を調べている

Bottigliengoらによる報告：
Oversampling and replacement strategies in propensity score matching: a critical review focused on small sample size in clinical settings | BMC Medical Research Methodology | Full Text
同じく、サンプルサイズが小さい場合に、1対1マッチングと1対多マッチング、復元マッチングと非復元マッチング*3との性能の違いを調べている

などがあります。

今回はPirracchioらの報告（以下、Pirracchio論文と書きます）について紹介するとともに、Rを使って再現シミュレーションを行なってみます。

サンプルサイズがかなり小さくても問題はないとのことだが...

Pirracchio論文では、処置群と対照群の2グループ間での比較を行う状況を想定し、グループ間での背景因子の偏りをマッチングやIPTWで補正することで2値アウトカムに関するオッズ比（対照群のオッズに対する、処置群のオッズの比）を正しく推定できるかどうかをシミュレーション実験により検討しています。
検討された各グループのサンプルサイズは最大で1000、最小で40でした。*4

全体的な結論として、傾向スコアのモデルが適切に設定されていれば、サンプルサイズが小さい場合でも（検討された範囲では、各グループ40でも）処置効果を正しく推定できるだろう、とされています。
具体的には、さまざまな設定のもとでも、処置効果の推定のバイアスはせいぜい10%以内であり、また第一種の過誤(Type 1 error)の生じる確率も名目値である5%を大きく超えることはない*5という結果でした。

シミュレーション

設定

Pirracchio論文ではデータの分布についてさまざまなシナリオを検討していますが、今回はTable1の一番左の列に記載の「共変量の効果は中程度（条件付きオッズ比1.5）、処置効果は強い（条件付きオッズ比2.5）」というシナリオのみ再現してみます。*6
設定について、Rでのコード例とともに説明します。

＜背景因子（共変量）＞
の4つがあるとします。それぞれ、互いに独立に平均、分散の正規分布に従います。
例えば以下のようにMASSパッケージのmvrnormでサンプリングができます。なおここでは各グループのサンプルサイズを100としています。

library(MASS)

n <- 100
X <- mvrnorm(n = 2*n, mu = rep(0, 4), Sigma = diag(rep(0.5^2, 4)))

＜処置の割り当て＞
は処置群の場合1を、対照群の場合0をとる変数です。以下のロジスティックモデルを通して、背景因子が割り当て確率に関連しているものとします。つまり、背景因子のうちが処置の割り当てに影響する状況を考えます。処置の割り当て比率が平均的に1:1になるよう、切片は0に設定されています。

以下では、まずロジスティックモデルのパラメータalphaを定義し、上の式の右辺を計算しています。次にその結果を確率に変換し、二項分布からをサンプリングします。

alpha_0 <- 0
alpha_1to4 <- c(0, 0, 0.41, 0.41)

logit_p_trt <- alpha_0 + X %*% alpha_1to4
p_trt <- 1 / (1 + exp(-logit_p_trt))

Z <- rbinom(n = 2*n, size = 1, prob = p_trt)

＜アウトカム＞
は関心ある2値アウトカムを表し、処置および共変量との関連はロジスティックモデルで表されるとします。はアウトカムのみに影響し、は割り当てとアウトカムの双方に影響する、いわゆる交絡因子となる状況です。
またの回帰係数0.92は、処置群の対照群に対する（条件付き）オッズ比が約2.5であることを意味しています。

なおは、1,000,000サンプルを用いて、アウトカムの発現割合が平均で50%になるように最適化計算で求めることとされています。計算方法は色々あるかと思いますが、ここでは最小二乗法と同じ考え方で以下の誤差、つまり「ロジスティックモデルによる予測確率と50%との誤差（=差の二乗和）」が最小になるような値をとしました。

beta_1to4 <- c(0, 0.41, 0, 0.41)
beta_T <- 0.92

# beta_0の決定
## 1,000,000サンプルの生成
n_p <- 1000000
X_p <- mvrnorm(n = n_p, mu = rep(0, 4), Sigma = diag(rep(0.5^2, 4)))
logit_p_trt_p <- alpha_0 + X_p %*% alpha_1to4
p_trt_p <- 1 / (1 + exp(-logit_p_trt_p))
Z_p <- rbinom(n = n_p, size = 1, prob = p_trt_p)

## 誤差関数
targetfunc <- function(b) {
  sum((1/(1+exp(-(b + Z_p*beta_T + X_p%*%beta_1to4))) - rep(0.5, n_p))^2)
}
## 誤差の最小化
opt <- optimize(targetfunc, interval = c(-5, 5))
beta_0 <- opt$minimum

# Yのサンプリング
logit_p_out <- rep(beta_0, 2*n) + beta_T * Z + X %*% beta_1to4
p_out <- 1 / (1 + exp(-logit_p_out))
Y <- rbinom(n = 2*n, size = 1, prob = p_out)

# データフレームに整理
simdf <- data.frame(ID = 1:(2*n), Z = Z, Y = Y,
                    X_1 = X[,1], X_2 = X[,2], X_3 = X[,3], X_4 = X[,4])

このようにして生成されたデータは、共変量が処置群・対照群の間でバランスしておらず、処置効果について交絡が生じています。そのため、傾向スコア法によって共変量のアンバランスを補正した解析を行います。
Pirracchio論文ではマッチングとIPTWの両方が検討されていますが、今回の再現ではIPTWのみを扱います。

今回は各グループのサンプルサイズが40、60、100、500の場合のIPTWの推定性能を確認しています。

ここで、IPTWで推定する対象は処置に関する周辺オッズ比となるのですが、周辺オッズ比は条件付きオッズ比のように回帰係数を指数変換するだけでは求められず、共変量についての積分計算が必要になります。
今回は切片を計算する際に使用した1,000,000サンプルを利用して、モンテカルロ法に基づく周辺オッズ比を算出しました（参考文献[2]や[4]を参照）。この値を各シミュレーションにおける真値として参照します。

## 1,000,000サンプル個々のアウトカム発現確率
logit_p_out_e <- rep(beta_0, n_p) + beta_T * Z_p + X_p %*% beta_1to4
p_out_e <- 1 / (1 + exp(-logit_p_out_e))

## 群ごとにアウトカム発現確率を平均
p_out_mean <- data.frame(p_out = p_out_e, Z = Z_p) %>%
group_by(Z) %>% summarise(p = mean(p_out))

## 周辺オッズ比
true_marginal_OR <- (p_out_mean[2, ]$p/(1-p_out_mean[2, ]$p))/(p_out_mean[1, ]$p/(1-p_out_mean[1, ]$p))

＜IPTW＞
ロジスティック回帰モデルなどによって推定した、処置に関する個人の傾向スコアをとするとき、各個人に以下の重みをつけて解析する方法がIPTWです。

つまり処置群に属する個人にはの重みが、対照群に属する個人にはの重みが与えられます*7。

傾向スコアを推定するためのモデルが正しく設定されているならば（交絡因子がすべて含まれているなど）、IPTWによって処置効果を正しく（ばらつきはあるが、バイアスなく）推定することができます。

Rで傾向スコアを用いたIPTWを実施する方法はいくつかありますが、今回は重みの計算にipwパッケージを使用し、重みづけ解析の部分はPirracchio論文と同様にsurveyパッケージで行いました。*8
ipwパッケージとsurveyパッケージを用いたIPTWの実行については以下の論文でも解説されているので、詳細はこちらをご参照ください。
ipw: An R Package for Inverse Probability Weighting | Journal of Statistical Software

以下のコード例では、最初にipwパッケージのipwpoint関数で重みの計算を行います。重みにもさまざまな種類がありますが、ここではPirracchio論文と同様の基本的なものを使用しました。
重みは元のデータフレームへ格納します。
次にsurveyパッケージのsvyglmを使用し、IPTWによるロジスティック回帰を行います。
最後に、回帰の出力結果をbroomパッケージのtidy関数を利用してデータフレームにまとめます。

library(ipw)
iptw <- ipwpoint(exposure = Z, family = "binomial", link = "logit",
                 numerator = ~ 1, denominator = ~ X_1 + X_2 + X_3 + X_4,
                 data = simdf, trunc = NULL)
simdf_w <- simdf %>% mutate(IPTW = iptw$ipw.weights)

library(survey)
fit <- svyglm(Y ~ Z, design = svydesign(id = ~ 1, weights = ~ IPTW, data = simdf_w),
              family = quasibinomial())

library(broom)
res <- fit %>% tidy() %>% filter(term == "Z")

次項でシミュレーション全体のコードと結果を報告します。

シミュレーション結果

ここまでの流れをシミュレーション用にまとめると、以下のようになります。

library(tidyverse)
library(broom)
library(MASS)
library(ipw)
library(survey)

# シミュレーション実行用関数
## nsim：シミュレーション反復数
## n：各グループのサンプルサイズ
## beta_T：処置に関する回帰係数の真値
sim <- function(nsim, n, beta_T){

  # ロジスティックモデルのパラメータ
  alpha_0 <- 0
  alpha_1to4 <- c(0, 0, 0.41, 0.41)
  beta_1to4 <- c(0, 0.41, 0, 0.41)
  beta_T <- beta_T
  
  # 最適化計算でbeta_0を決めます
  n_p <- 1000000
  X_p <- mvrnorm(n = n_p, mu = rep(0, 4), Sigma = diag(rep(0.5^2, 4)))
  logit_p_trt_p <- alpha_0 + X_p %*% alpha_1to4
  p_trt_p <- 1 / (1 + exp(-logit_p_trt_p))
  Z_p <- rbinom(n = n_p, size = 1, prob = p_trt_p)

  targetfunc <- function(b) {
    sum((1/(1+exp(-(b + Z_p*beta_T + X_p%*%beta_1to4))) - rep(0.5, n_p))^2)
  }
  opt <- optimize(targetfunc, interval = c(-5, 5))
  beta_0 <- opt$minimum

  # 周辺オッズ比の算出
  logit_p_out_e <- rep(beta_0, n_p) + beta_T * Z_p + X_p %*% beta_1to4
  p_out_e <- 1 / (1 + exp(-logit_p_out_e))
  p_out_mean <- data.frame(p_out = p_out_e, Z = Z_p) %>%
    group_by(Z) %>% summarise(p = mean(p_out))
  true_marginal_OR <- (p_out_mean[2, ]$p/(1-p_out_mean[2, ]$p))/(p_out_mean[1, ]$p/(1-p_out_mean[1, ]$p))

  # 結果を格納するデータフレームを作っておきます
  sim_result <- data.frame(n = rep(n, nsim),
                           beta_T = rep(beta_T, nsim),
                           true_or = rep(true_marginal_OR, nsim),
                           estimate = rep(0, nsim),
                           p.value = rep(0, nsim))
  
  # シミュレーション反復開始です
  for (i in 1:nsim){
    ## データを生成します
    X <- mvrnorm(n = 2*n, mu = rep(0, 4), Sigma = diag(rep(0.5^2, 4)))

    logit_p_trt <- alpha_0 + X %*% alpha_1to4
    p_trt <- 1 / (1 + exp(-logit_p_trt))
    Z <- rbinom(n = 2*n, size = 1, prob = p_trt)

    logit_p_out <- rep(beta_0, 2*n) + beta_T * Z + X %*% beta_1to4
    p_out <- 1 / (1 + exp(-logit_p_out))
    Y <- rbinom(n = 2*n, size = 1, prob = p_out)

    simdf <- data.frame(ID = 1:(2*n), Z = Z, Y = Y, 
                        X_1 = X[,1], X_2 = X[,2], X_3 = X[,3], X_4 = X[,4])

    ## IPTWで解析します
    iptw <- ipwpoint(exposure = Z, family = "binomial", link = "logit",
                     numerator = ~ 1, denominator = ~ X_1 + X_2 + X_3 + X_4,
                     data = simdf, trunc = NULL)
    simdf_w <- simdf %>% mutate(IPTW = iptw$ipw.weights)

    fit <- svyglm(Y ~ Z, design = svydesign(id = ~ 1, weights = ~ IPTW, data = simdf_w),
                    family = quasibinomial())
    res <- fit %>% tidy() %>% filter(term == "Z")

    ## 結果を格納します
    sim_result[i,]$estimate <- res$estimate
    sim_result[i,]$p.value <- res$p.value
  }
  return(sim_result)
}

IPTWの性能評価の指標として、Pirracchio論文で検討されているもののうち、以下の項目を確認することにします。

• Type1 errorの確率：処置効果がないのに、統計的有意に効果ありと判断してしまう確率。今回は両側5%に設定しているものとします。
• Bias：処置効果の推定値と、真の処置効果とに平均的にどれだけズレがあるかを表す。報告では数式は記載されていないが、により計算していると思われます。は処置効果（今回はオッズ比で示しています）の推定値のシミュレーションを通した平均、は真の処置効果で、モンテカルロ法で算出した結果おおむね2.56程度になりました。
• Percent bias：バイアスをパーセント表示したものです。こちらも明記はありませんが、で計算していると考えられます。

シミュレーション結果を出力するために、今回は以下のコードを用いました。結果を表形式で出力するためにgtパッケージを使用しています。
サンプルサイズ（40, 60, 100, 500）と回帰係数の値（Type1 errorの評価の場合0、バイアス評価の場合0.92）について複数の条件で実験を行うので、furrrパッケージにより並列処理を行うことにしました（参考文献[5]や[6]を参照）。最後のあたりは汚いコードになってしまいすみません。
furrrパッケージ、purrrパッケージで何をやっているのかについてはまた別の機会に書ければと思います。

library(furrr)
library(tictoc) #このパッケージで処理にかかった時間を測れます

# シミュレーション設定をデータフレームにする
## tidyrパッケージのexpand_gridを使用
sim_params <- expand_grid(
  nsim = 7300,
  n = c(40, 60, 100, 500),
  beta_T = c(0, 0.92)
)

# 各設定でのシミュレーション実行
plan(multisession) # 並列処理
tic() # tic() toc()で時間を測る
result <- future_pmap_dfr(.l = sim_params, .f = sim,
                          .options = furrr_options(seed = 123L),
                          .progress = TRUE)
toc()

# シミュレーション結果を表にする
## Pirracchio論文の結果
bmc_result <- data.frame(N = rep(c("N = 40", "N = 60", "N = 100", "N = 500"), each = 3),
                         Measure = rep(c("Type I error", "Bias", "Percent bias"), 4),
                         IPTW_BMC = c(0.048, 0.057, 6.5, 0.046, 0.036, 4,
                                   0.046, 0.018, 2, 0.046, 0.0007, 0.8))
## 今回のシミュレーションの結果
result_sum <- result %>%
  mutate(est_or = exp(estimate),
         reject = case_when(p.value < 0.05 ~ 1, TRUE ~ 0)) %>%
  group_by(n, beta_T) %>%
  summarise(true_or = mean(true_or),
            est_or = mean(est_or),
            alphaerror_power = mean(reject)) %>%
  mutate(bias = est_or - true_or,
         relbias = (bias/true_or)*100)
sim_null <- result_sum %>% filter(beta_T == 0.00) %>%
  dplyr::select(n, alphaerror_power)
sim_alt <- result_sum %>% filter(beta_T == 0.92) %>%
  dplyr::select(n, bias, relbias)
sim_result <- inner_join(sim_null, sim_alt, by = "n") %>%
  pivot_longer(cols = c(alphaerror_power, bias, relbias),
               names_to = "Measure", values_to = "IPTW_SIM")

all_result <- bmc_result %>% mutate(IPTW_SIM = sim_result$IPTW_SIM)

## 表の作成と保存
library(gt)
res_tbl <- gt(all_result, groupname_col = "N", rowname_col = "Measure") %>%
  fmt_number(columns = c("IPTW_BMC", "IPTW_SIM"), decimals = 3)
gtsave(res_tbl, "sim_restbl_20220411.png")

シミュレーション結果は以下の通りです。
左側（IPTW_BMC）にPirracchio論文での数値を、右側（IPTW_SIM）に今回のシミュレーションで得られた数値を表示しました。

シミュレーション結果

Type1 errorの確率については、今回のシミュレーションでも全てのサンプルサイズで指定した水準の5%を下回っていました。
サンプルサイズが小さい時にType1 errorの確率が増加してしまうのは他の統計手法ではありがちなのですが、IPTWに関しては、サンプルサイズが各グループ40程度でも（今回の設定の範囲、例えば共変量の数が4つだったり、共変量どうしの相関がほぼないような場合においてではありますが）その危険性は小さいように思います。

バイアスについては「Percent bias」を見てみましょう。今回の実験では、サンプルサイズが各グループ40の時にはPirracchio論文と比べ推定のバイアスが2倍程度になっていました。
特にPirracchio論文では「サンプルサイズが40でもバイアスは10%を下回る」ことが述べられていたのですが、シミュレーションでは13%ほどと少し大きめの結果になりました。これはオッズ比のスケールで表しているので、おおざっぱに言うと、真のオッズ比が2.56であるところを2.89（2.56の1.13倍）と推定していると理解できます。*9
一方、各グループのサンプルサイズが100の場合にはPirracchio論文に近い値に、500の場合では過小推定の方向に若干のバイアスが生じる結果になりました。しかしながらそこまで深刻なバイアスは生じないだろうことが伺えます。

おわりに

サンプルサイズが小さい場合に傾向スコア解析を行うとどうなるのかについて、いくつかの研究報告があるようです。
今回は、比較的古い報告であるPirracchioらの結果を紹介し、IPTWの評価結果の一部についてRで再現シミュレーションを行いました。

おおむね近い結果は得られたように思いますが、サンプルサイズが各グループ40〜60の場合には報告されている結果の2倍近いバイアスが確認されました。Pirracchio論文とはシミュレーションコードや設定条件が異なるためかもしれませんし、今回の反復回数では十分な精度が得られなかった可能性もあります。
また、共変量の数や相関の程度、さらにIPTWの方法（用いる重みなど）によっても結果は異なってくると考えられます。

一応、今回の結果を踏まえると、サンプルサイズが非常に小さい場合には多少のバイアスが生じる可能性があると思っておいた方が無難なのかもしれません。

参考文献

[1] Pirracchio, R., Resche-Rigon, M., & Chevret, S. (2012). Evaluation of the propensity score methods for estimating marginal odds ratios in case of small sample size. BMC medical research methodology, 12(1), 1-10.
[2] Bottigliengo, D., Baldi, I., Lanera, C., Lorenzoni, G., Bejko, J., Bottio, T., ... & Gregori, D. (2021). Oversampling and replacement strategies in propensity score matching: a critical review focused on small sample size in clinical settings. BMC medical research methodology, 21(1), 1-16.
[3] van der Wal, W. M., & Geskus, R. B. (2011). ipw: an R package for inverse probability weighting. Journal of Statistical Software, 43, 1-23.
[4] Austin, P. C., & Stafford, J. (2008). The performance of two data-generation processes for data with specified marginal treatment odds ratios. Communications in Statistics—Simulation and Computation®, 37(6), 1039-1051.
[5] furrr パッケージで R で簡単並列処理 | Atusy's blog
[6] Monte Carlo Simulations: Going parallel with the furrr package

*1:傾向スコアについては優れた解説が色々なところで見つかるので、今回は説明を省略します。また機会があればここでも書きたいと思います。

*2:具体的な数は諸説あります。

*3:マッチングは処置群のある個体に対して対照群の似たような個体をマッチング相手として見つける方法ですが、復元マッチングとは、一度マッチング相手となった個体を、他の処置群の個体のマッチング候補として再利用することを言います。非復元マッチングでは、一度マッチングされた個体は以降はマッチング候補として使用されません。

*4:サンプルサイズの数値がグループごとなのかグループ合わせた合計なのかは明記されていませんでしたが、文中の記述からはグループごとの数値と思われますので、再現シミュレーションもそれを前提に行いました。

*5:有限回のシミュレーションによる推定なので、誤差によって5%を少しだけ超えることはあります。

*6:「他の共変量をある特定の値に固定したときの」オッズ比のことです。これに対して、「他の共変量について、全個人の平均をとったときの」オッズ比である周辺オッズ比という概念もあり、両者は必ずしも一致しません。前者はある共変量の値をもつ特定の個人についての効果量、後者は集団全体での効果量を意味しています。

*7:おおざっぱに言えば「処置群に入りそうにないような特徴を持つ個人のデータには、その珍しさに応じた重みをつける」ことによって、そのような特徴を持つ人の人数が対照群と同じくらいになるような補正を行っています（対照群でも同様）。

*8:重みづけ解析を行う方法にも色々と選択肢があり、注意が必要と言われているのですが、今回の本題とは外れるので別の機会に書ければと思います。

*9:実際には2.89は「同じようなデータを得て、同じ解析を行う」ことを何度も繰り返した時の平均なので、あくまで傾向ではあります。

線形回帰の説明変数は何個まで入れられるのか

はじめに

線形回帰（重回帰）やロジスティック回帰、Cox比例ハザードモデルなどを使う上で突きあたる実用上の問題の一つに、「説明変数の数を何個まで入れていいのか？」というものがあります。
結果に影響しそうな因子は色々と考えつくことが多いため、できる限り説明変数を入れたくなるのですが（そのような因子を探索するのがそもそもの目的である場合はなおさら）、サンプル数に対して説明変数の数が多すぎると推定精度の低下や過剰適合(Overfitting)といった問題が生じがちになります。

適切な説明変数の数について、ロジスティック回帰およびCox比例ハザードモデルでは「1つの説明変数につき、イベント数が10必要*1」というよく知られた基準が存在しますが（参考文献[1]と[2]）、線形回帰の場合にはどうなのだろう？そういえば聞いたことがないな、と思い調べてみました。

今回は、2015年にJournal of Clinical Epidemiologyという雑誌に掲載されたAustin and Steyerbergの論文（参考文献[3]）で報告されている結果を紹介します。
結論から言うと、線形回帰の場合には説明変数1つにつきサンプル数が最低2ほどあれば適切な推定結果が得られるだろう、ということです。つまり、例えばサンプル数が30の時には説明変数は15個まで入れられることになります。
ただし、あくまで今回のシミュレーションで設定された状況における結果であるため、実際の解析では可能であれば十分なサンプル数を用意する、あるいは説明変数の数を必要以上に多くしないほうが無難かと個人的には思います。

Austin and Steyerberg(2015)による研究報告

この論文では、ロジスティック回帰やCox比例ハザードモデルにおける「説明変数1つにつきイベント数10」を報告した研究と同じデータをベースにしたシミュレーションを行い*2、説明変数1つに対するサンプル数が1〜50それぞれの場合に回帰係数の推定値や標準誤差などにどの程度のバイアスが生じるかが検討されています。

シミュレーションによって

• 回帰係数の推定値にバイアスが生じるかどうか
• 回帰係数の標準誤差にバイアスが生じるかどうか
• 回帰係数の信頼区間が名目の値(95%)通りになるかどうか
• 決定係数と自由度調整決定係数にバイアスが生じるかどうか

を評価した結果、サンプル数がいかなる場合でも決定係数以外には深刻なバイアスはほとんど生じないというものでした（説明変数の数とサンプル数が同じ場合のみ、一部の回帰係数の推定値に若干大きめのバイアスが生じていました）。
この結果を踏まえ、「説明変数1個につき、サンプル数は2ほど必要」と結論されています。
なお論文著者らが独自に設定したシミュレーションデータにおいても、同様の結果が得られたことが記載されています。

ということで、ロジスティック回帰やCox比例ハザードモデルと比べ、線形回帰の場合は説明変数の個数についてはそれほど神経質になる必要はなさそうですが、今回検討されたのは説明変数の多重共線性（強い相関のある説明変数の組み合わせが存在すること）が問題にならないようなデータであり*3、多重共線性が無視できないような場合には異なる結果が得られるかもしれない、と述べられています。

ロジスティック回帰においては、許容される説明変数の数は一概には言えず、説明変数どうしの相関の強さや回帰係数の大きさなどに依存するという報告があります（参考文献[4]）。線形回帰の場合もケースバイケースであると考え、場合によっては1変数あたり2サンプルでも大丈夫、程度に考えておいたほうがよいかもしれません。

参考文献

[1] Peduzzi, P., Concato, J., Feinstein, A. R., & Holford, T. R. (1995). Importance of events per independent variable in proportional hazards regression analysis II. Accuracy and precision of regression estimates. Journal of clinical epidemiology, 48(12), 1503-1510.
[2] Peduzzi, P., Concato, J., Kemper, E., Holford, T. R., & Feinstein, A. R. (1996). A simulation study of the number of events per variable in logistic regression analysis. Journal of clinical epidemiology, 49(12), 1373-1379.
[3] Austin, P. C., & Steyerberg, E. W. (2015). The number of subjects per variable required in linear regression analyses. Journal of clinical epidemiology, 68(6), 627-636.
[4] Courvoisier, D. S., Combescure, C., Agoritsas, T., Gayet-Ageron, A., & Perneger, T. V. (2011). Performance of logistic regression modeling: beyond the number of events per variable, the role of data structure. Journal of clinical epidemiology, 64(9), 993-1000.

*1:より正確には、ロジスティック回帰の場合は2値の目的変数の「あり・なし」カテゴリーのうち少ない方に該当するサンプル数が10、Cox比例ハザードモデルの場合は打ち切りされていない（イベントが生じた）サンプル数が10必要です。

*2:元となっているのは現実のデータではありますが、評価にあたってはシミュレーションでデータを作っているので、真の値はわかっている状態です。

*3:詳しくは、どの説明変数の分散拡大因子(Variance inflation factor)も1.1未満だったとのことです。

カッパ係数とその難点

はじめに

心理的な特性の評価や、疾患の重症度の判定など、僕たちの身の回りには何らかの評価を行うためのさまざまな検査方法があります。
例えば学校や企業の採用試験などで適正検査というものを受けさせられた経験もあるかと思います。
これらの検査は決して適当に作られている訳ではなく、開発の段階で「時間を空けて同じ人を再検査したとしても、同じ結果になること」や「同じ人を異なる判定者が判定したとしても、同じ結果になること」を確かめる作業を行なっています。このことは信頼性(Reliability)の評価と呼ばれます。

今回は、信頼性を評価するための統計的指標のうち、カテゴリカルデータの場合に頻用されるカッパ係数(Kappa coefficient)について説明します。
カテゴリカルデータの場合というのは、検査による判定結果が「病気のあり・なし」（2値）であったり、1〜5の5段階評価（順序）であったりする場合に当たります。
今回は話を簡単にするために、判定が2値の場合について説明していきたいと思います。この場合のカッパ係数はCohen（コーエン）のカッパ係数と呼ぶことがあります*1。

状況設定

今回はSim and Wrightによる論文（参考文献1）の数値例を、より身近な例に置き換えて考えます。

ある企業では、入社希望者の採用選考の初期段階において

• 採用しても良いかもしれないので、応募者を次の選考ステップへ進める
• 明らかに採用すべきではないので、応募者を不採用とする

のいずれかの判断を行うためのチェックリストを作成しました。
しかしながら、このチェックリストを使った場合に採用担当者によって異なった判断がなされる恐れはないか？という意見が出たため、チェックリストの運用を始める前にその信頼性を評価することになりました*2。

そこで、実際の採用選考でチェックリストを使用し、信頼性を評価するためのデータ収集を行うこととしました。
39人の応募者に対して、2人の人事部員、AさんとBさんがチェックリストに沿った判断を行いました。結果は次の表のようになりました。

		人事部員Bさん
		採用	不採用	合計
人事部員Aさん	採用	22	2	24
	不採用	4	11	15
	合計	26	13	39

直感的には、2人の採用・不採用の判断はほとんど一致しており、チェックリストはうまく作られていると言えそうです。一致した人数の総人数に占める割合を計算するとであり、84.62%の応募者に対して両者の判断が一致していました。

しかしながら、一致した2人の判断のうち、ある程度は偶然による可能性があります。
このデータによると、Aさんが採用と判断した割合は、Bさんが採用と判断した割合はでした。ここで、もし仮に「このチェックリストには異なる担当者の判断を一致させる効果が全くない」と仮定すると*3、たまたま両者ともに採用と判断する応募者の割合は（41.03%）と考えられます。同様に、偶然両者が不採用と判断する割合は（12.82%）です。
よって、今回のケースでは偶然2人の判断が一致する可能性は（53.85%）ほどあったことになります。

このように、もしチェックリストが採用判断の統一には役に立たないものだったとしても、半数以上の応募者についてはたまたま採否の判断が一致すると考えられるため、今回の一致の割合84.62%をもって信頼性が十分との結論を下すのは少し難しいかもしれません。
このようなとき、カッパ係数を用いることにより「偶然を超えた一致の度合い」を評価することができます。

カッパ係数とは

カッパ係数は、以下の式で定義される指標です。なおカッパとはギリシャ文字ののことをいいます。

ここでは観測された一致割合であり、先ほどの例では0.8462です。または「偶然起こりうる一致の割合」を指し、同じく先の例では0.5385と計算されていました。
カッパ係数の意味あいは以下のように解釈することができます。

つまり、偶然による影響を取り除いて、どの程度の一致が得られたかを測っています。

今回のデータからカッパ係数を計算すると以下のようになります。

カッパ係数の計算はどの統計ソフトにも実装されているかと思いますが、Rでは例えばirrパッケージを使って計算できます。コード例と、上記のデータ例を用いて計算した結果は以下の通りです（ごく単純な例ですみません）。

コード例

library(irr)

ad = data.frame(
  rator1 = c(rep("accept", 24), rep("reject", 15)),
  rator2 = c(rep("accept", 22), rep("reject", 2), rep("accept", 4), rep("reject", 11))
)

table(ad$rator1, ad$rator2)
kappa2(ad)

出力

> table(ad$rator1, ad$rator2)
        
         accept reject
  accept     22      2
  reject      4     11

> kappa2(ad)
 Cohen's Kappa for 2 Raters (Weights: unweighted)

 Subjects = 39 
   Raters = 2 
    Kappa = 0.667 

        z = 4.19 
  p-value = 2.8e-05 

カッパ係数の数値をそのまま解釈するのは少し難しいのですが、経験的な基準がいくつか知られています。
例えばLandis and Kochによる論文（参考文献2）で示された以下のものが有名です（日本語訳は筆者による）。

カッパ係数	一致の強さ
<0.00	Poor（不十分）
0.00 - 0.20	Slight（わずか）
0.21 - 0.40	Fair（まずまず）
0.41 - 0.60	Moderate（中くらい）
0.61 - 0.80	Substantial（かなり）
0.81 - 1.00	Almost Perfect（ほぼ完全）

このように、偶然判断が一致する可能性を考慮に入れて評価できることがカッパ係数の利点なのですが、データの性質によっては思わぬ結果が得られる場合があることが知られています。

カッパ係数の難点

Prevalenceの影響

まず、得られたデータが以下のようだった場合を考えてみます。*4
（例1-1）

		人事部員Bさん
		採用	不採用	合計
人事部員Aさん	採用	28	3	31
	不採用	6	2	8
	合計	34	5	39

両者の判断が一致した割合はで、かなりの一致が見られています。ところが、偶然による一致を計算するとと大きな値であり、一致のかなりの部分が偶然によるものである可能性を否定できません。
この時カッパ係数は

と非常に小さい値になってしまいます。

一方、次のような結果が得られたとしたらどうでしょうか。
（例1-2）

		人事部員Bさん
		採用	不採用	合計
人事部員Aさん	採用	15	3	18
	不採用	6	15	21
	合計	21	18	39

両者の判断が一致した割合は例1-1と同じくですが、偶然による一致はほどであり、カッパ係数は

です。このように、例1-1と例1-2では、観測された一致割合は同じですが、カッパ係数は大きく異なります。

例1-2では一致のうち採用と不採用はともに15人となりましたが、例1-1では採用との判断が一致したのは28人、不採用との判断が一致したのは2人で、大きな偏りがあります。今回の例での採用・不採用の頻度のことを「prevalence」*5と呼び、カッパ係数に影響を与える要因の一つとして知られています。prevalenceの不均衡が大きい（今回の例では採用と不採用の頻度の差が大きい）ほど、偶然による一致の可能性が大きくなるため、カッパ係数は小さい値をとる傾向にあります。

Biasの影響

今度は、以下のようなデータを考えます。

（例2-1）

		人事部員Bさん
		採用	不採用	合計
人事部員Aさん	採用	29	21	50
	不採用	23	27	50
	合計	52	48	100

（例2-2）

		人事部員Bさん
		採用	不採用	合計
人事部員Aさん	採用	29	6	35
	不採用	38	27	65
	合計	67	33	100

どちらの例も判断が一致した人数は採用29人・不採用27人で同じであり、その割合はです。一方、例2-1では採用・不採用と判断した人数がAさんとBさんでほとんど同じであるのに対し、例2-2ではAさんは半数以上を不採用、Bさんは半数以上を採用と判断しています。

まずは偶然による一致の割合を計算してみると、次のようになります。
（例2-1）：
（例2-2）：

よって、カッパ係数は次のようになります。
（例2-1）：
（例2-2）：

このように、採用・不採用と判断する割合が2人の間で異なるほど、カッパ係数は大きい値をとる傾向があることが知られています。この割合の相違の程度は「bias」と呼ばれています。

難点にどう対処するか

これら2つの影響を取り除いて評価するために、カッパ係数を調整するPABAK(Prevalence-adjusted Bias-adjusted Kappa)という方法が提案されています（参考文献3）。PABAKは、PrevalenceとBiasの問題が生じないような状況を想定し、もしそうであった場合に得られるであろうカッパ係数を計算します。
ただし、実際に得られたデータではなく仮想的な状況を考えているため、PABAK単体では意味をなさないのではないかという批判もあります。
参考文献1でも述べられているように、実際には、オリジナルのカッパ係数とPABAKをあわせて報告したり、PrevalenceやBiasがどの程度か・カッパ係数にはどの程度の影響を与えているのか、等の考察を加えることが必要になってくるかと思います。

まとめ

今回は、ある検査方法の信頼性を測る統計的指標であるカッパ係数について紹介しました。
カッパ係数にはさまざまな拡張がありますが、最も基本的なものは、異なる2名の判定が偶然を超えてどの程度一致するかを評価することを目的とします。単なる偶然の影響を除いた評価を行えるというところがポイントですが、一方でPrevalenceとBiasに影響を受けることが知られており、計算したカッパ係数の解釈には注意が必要と言えます。

参考文献

[1] Sim, J., & Wright, C. C. (2005). The kappa statistic in reliability studies: use, interpretation, and sample size requirements. Physical therapy, 85(3), 257-268.
[2] Landis, J. R., & Koch, G. G. (1977). The measurement of observer agreement for categorical data. biometrics, 159-174.
[3] Byrt, T., Bishop, J., & Carlin, J. B. (1993). Bias, prevalence and kappa. Journal of clinical epidemiology, 46(5), 423-429.

*1:判定結果が順序カテゴリー、例えば5段階評価のような場合には、2値の場合のカッパ係数を拡張した重み付きカッパ係数(Weighted Kappa coefficient)というものが使われます。

*2:チェックリストの内容の妥当性については別途検討されているものとします。

*3:つまり、2人の判断は統計的に独立と仮定しています。以下の計算では、独立な場合の同時確率の性質を用いています。

*4:本セクションの数値例も、参考文献1のものを使わせていただきました。

*5:医学分野では「有病率」と訳されることが多く、その文脈では、ある時点において関心ある集団内で疾患にかかっている人の割合を指します。「疾患のあり・なし」を判定するような場合をイメージするとしっくりくるかと思います。

ギブス・サンプリングの実装練習：(1-3)分散成分の事前分布を半コーシー分布にする

はじめに

これまで2回にわたってランダム効果モデルのギブス・サンプリングを説明してきました。またランダム効果の分散について、事前分布として逆ガンマ分布や一様分布を設定した場合のベイズ推定結果をシミュレーションにより確認しました。

ところが、分散パラメータの推定に関して、推定に使用できるデータ数が少ない場合には逆ガンマ分布や一様分布ではうまくいかない可能性があることが知られています。
そこで、今回は最終回として、Gelman(2006)（参考文献[1]）で紹介されている「半コーシー分布(Half Cauchy distribution)」を分散の平方根（以下では「標準偏差」と言うことにします）の事前分布にすることを考えてみます*1。
この分布はコーシー分布の範囲を正の値に限定したもので、右裾の厚い形状の分布形を持ちます。
特に標準偏差に関してある程度の事前情報があるような場合（例えば、ばらつきの大きさはどれだけ大きくても10程度だろう）には、逆ガンマ分布や一様分布よりも推奨されています。

今回は、まず半コーシー分布について簡単に紹介した後、前回と同じようにギブス・サンプリングに必要な完全条件付き分布を確認します。
またRでのサンプリングコード例とともにシミュレーション結果を報告します。

なお、半コーシー分布を事前分布に設定するのは、例えばStanのようなソフトウェアであれば比較的簡単に行えるのですが、ギブス・サンプリングを自分で実装するにはちょっとした工夫が必要になります。
Gelman論文を参考に、そのあたりの解説も行っていきます。

半コーシー分布とは

半コーシー分布は、以下の確率密度関数をもつ分布です（参考文献[3]）。

ただしにおける確率密度はです。
は分布の位置を決めるパラメータで、標準偏差の事前分布とする場合は通常のものが使われます。本記事でも以降はとしたものを考えることにします。
または分布の山の部分の広がりを決めるパラメータです（以下、スケールパラメータと呼ぶことにします）。このパラメータの値は定数として与えることも、さらに事前分布を考えることもあります。定数とする場合、例えば想定される標準偏差の大きさよりも少し大きめの値を設定します。

半コーシー分布の確率密度関数

今回は、ランダム効果が正規分布に従うとするモデルにて、標準偏差の事前分布を半コーシー分布とすることを考えます。

ところで、通常のコーシー分布については、次のような性質があります（参考文献[4]）。

1. を標準正規分布に従う確率変数、をパラメータの逆ガンマ分布に従う確率変数とする。この時、はスケールパラメータのコーシー分布に従う*2。
2. スケールパラメータのコーシー分布に従う変数に定数を掛けたものは、スケールパラメータのコーシー分布に従う（はの絶対値）。

この2つの性質から、「正規分布に従う変数」と、「パラメータの逆ガンマ分布に従う変数の平方根」とを掛けたものは以下の変形によりスケールパラメータのコーシー分布に従うことがわかります*3。

のとる値を正の値に制限した場合には、の分布はスケールパラメータの半コーシー分布になります。
少しややこしい話になりましたが、この性質を利用することで、この後のギブス・サンプリングをうまく進めることができるようになります。

完全条件付き分布

半コーシー分布を設定した場合のギブス・サンプリングですが、サンプリングに必要となる完全条件付き分布を得るためには、元々のランダム効果モデルの表現を少し修正する必要があります。と言っても構造を変更して全く別のモデルにするわけではなく、用いられているパラメータの変換によって同じモデルを別の表現に直します。
ここで行う変換は「Parameter expansion」と呼ばれているものの一種で、サンプリングの高速化と真の分布への収束を良くするために古くから提案されているものです。

元のモデルは、観測値が以下の式で表されるとするものでした。

ただしです。

ここで、ランダム効果を以下のように変換します。

この時の（を与えた条件付きでの）分散は

となるので、という対応関係が成り立ちます。

さて、の事前分布を正規分布、の事前分布をパラメータの逆ガンマ分布とすると、半コーシー分布の紹介のところで述べたようにとを掛けたはスケールパラメータの半コーシー分布に従います。
さらにはそれぞれ他の全てのパラメータと観測値に対して「条件付き共役(conditionally conjugate)」、つまり完全条件付き分布も同じくは正規分布、は逆ガンマ分布になることが知られています。

したがって、正規分布と逆ガンマ分布だけを用いたギブス・サンプリングによりのサンプリングを（他のパラメータとともに）行い、各反復で得られるサンプルを用いてを計算することで、事前分布を半コーシー分布とするの（事後分布からの）サンプルが得られるというわけです*4。

サンプリングに必要な完全条件付き分布の導出は、前の2記事と同様に地道に数式を展開していけばできますので、結果だけ紹介することにします。
ただし、各パラメータの事前分布は以下のように定義します。

なおは定数とします。が半コーシー分布の広がりを決めるスケールパラメータになります。

の完全条件付き分布

以下の平均・分散パラメータをもつ正規分布になります。
平均：
分散：

の完全条件付き分布

パラメータの逆ガンマ分布になります。

の完全条件付き分布

パラメータの逆ガンマ分布になります。

の完全条件付き分布

以下の平均・分散パラメータをもつ正規分布になります。
平均：
分散：

の完全条件付き分布

以下の平均ベクトル・共分散行列をもつ多変量正規分布になります。
平均ベクトル：
共分散行列：
ただし、は1を並べたベクトルです。

ギブス・サンプリングではこれらの分布から順番にサンプリングを行いますが、各反復の最後に現時点のサンプルを用いて以下の変換式での事後サンプルを得ます。

では、Rで実装してみましょう。

Rコードとシミュレーション結果

今回の設定でのギブス・サンプリングは、例えば以下のようなコードで実行できます。
基本的な内容は逆ガンマ分布や一様分布の場合と同様ですが、サンプリングステップの最後（forループの最後のあたり）でとを他のパラメータサンプルを用いて計算しています（ただし、今回はの結果は確認していません）。

library(tidyverse)
library(MASS)
library(MCMCpack)

set.seed(819)

#----- sample data -----
K = 6 # number of subjects
J = 5 # obs per subject
mu = 5
s2_theta = 4
s2_e = 16

theta = rnorm(K, mean = mu, sd = sqrt(s2_theta))
e = rnorm(K*J, mean = 0, sd = sqrt(s2_e))
Y = rep(theta, each = J) + e
Ymat = matrix(Y, nrow = K, ncol = J, byrow = T)
Ybar = apply(Ymat, 1, mean) # Yの各個人の平均

#----- Gibbs sampling(Half-Cauchy) -----
# MCMC設定
nsamp = 11000
burnin = 1000
thin = seq(burnin+1, nsamp, by = 1)

# hyperparameter
# mu
mu_0 = 0
s2_0 = 10000
# xi
s2_xi = 20^2 # sqrtがHalf-Cauchyのscaleになる
# sigma_e
a_e = 0.001
b_e = 0.001
# sigma_eta
a_et = 1/2
b_et = 1/2

# 結果の入れ物
xi_s = array(NA, length(thin))
s2_eta_s = array(NA, length(thin))
s2_e_s = array(NA, length(thin))
mu_s = array(NA, length(thin))
eta_s = array(NA, c(K, length(thin)))
s2_theta_s = array(NA, length(thin)) # sampleから導出
theta_s = array(NA, c(K, length(thin))) # sampleから導出

# Gibbs sampling初期値
xi_g = runif(1, min = -2, max = 2)
s2_eta_g = runif(1, min = 0, max = 2)
s2_e_g = runif(1, min = 0, max = 2)
mu_g = runif(1, min = -2, max = 2)
eta_g = runif(K, min = -2, max = 2)

### sampling
for(s in 1:nsamp){
  if((round(s/500) - (s/500)) == 0){print(s)}
  # xi
  a = (s2_xi*sum((Y-rep(mu_g, K*J))*rep(eta_g, each = J)))/(J*s2_xi*sum(eta_g^2)+s2_e_g)
  b = (s2_e_g*s2_xi)/(J*s2_xi*sum(eta_g^2)+s2_e_g)
  xi_g = rnorm(1, mean = a, sd = sqrt(b))
  xi_s[s==thin] = xi_g

  # s2_eta
  a = a_et + K/2
  b = b_et + sum(eta_g^2)/2
  s2_eta_g = rinvgamma(1, a, b) # MCMCpack
  s2_eta_s[s==thin] = s2_eta_g
  
  # s2_e
  a = a_e + (K*J)/2
  b = b_e + sum((Y-rep(mu_g, K*J)-xi_g*rep(eta_g, each = J))^2)/2
  s2_e_g = rinvgamma(1, a, b)
  s2_e_s[s==thin] = s2_e_g
  
  # mu
  a = (s2_0*sum(Y-xi_g*rep(eta_g, each = J))+s2_e_g*mu_0)/(K*J*s2_0+s2_e_g)
  b = (s2_0*s2_e_g)/(K*J*s2_0+s2_e_g)
  mu_g = rnorm(1, mean = a, sd = sqrt(b))
  mu_s[s==thin] = mu_g
  
  # eta
  coef1 = (s2_e_g*s2_eta_g)/(J*s2_eta_g*(xi_g^2)+s2_e_g)
  coef2 = (J*xi_g)/s2_e_g
  a = coef1 * coef2 * (Ybar - rep(mu_g, K))
  b = diag(rep(coef1, K))
  eta_g = mvrnorm(1, mu = a, Sigma = b)
  eta_s[, s==thin] = eta_g
  
  # s2_theta
  s2_theta_g = (abs(xi_g) * sqrt(s2_eta_g))^2
  s2_theta_s[s==thin] = s2_theta_g
  
  # theta
  theta_g = mu_g + xi_g * eta_g
  theta_s[s==thin] = theta_g
}

さて、今回は

1. 半コーシー分布
2. 逆ガンマ分布
3. 一様分布

のそれぞれを事前分布にした場合ののサンプリング結果を比較してみます。
なお、半コーシー分布は上記コード例の通りスケールパラメータを20（真の値である4の5倍）としました。また逆ガンマ分布と一様分布は無情報分布として用いることを想定し、逆ガンマ分布のパラメータは、一様分布の範囲はに設定しました*5。
半コーシー分布の場合のプロットの作図コード例は以下の通りです。今回も稀にとても大きな値がサンプリングされるので、表示範囲を0〜20に制限しています。

val = s2_theta_s
s2_theta_df = as.data.frame(val) %>%
  mutate(Iter = 1:length(thin))
ggplot(s2_theta_df, aes(x = Iter, y = val)) + geom_line() +
  geom_hline(yintercept = s2_theta, color = "red") +
  ylim(c(0, 20)) +
  labs(y = "sigma^2_theta", title = "Half-Cauchy prior") + theme_bw()

トレースプロットを(1)半コーシー分布、(2)逆ガンマ分布、(3)一様分布、の順に示します。

(1)半コーシー分布の場合のトレースプロット

(2)逆ガンマ分布の場合のトレースプロット

(3)一様分布の場合のトレースプロット

他の場合と比べて、半コーシー分布を事前分布とした場合は真の値（赤色の直線で表示）に近いところにサンプルが集まっているように見えます。

サンプルから推定される事後分布の要約統計量は次のようになりました。

事前分布	平均値	中央値	95%信用区間
半コーシー分布	4.27	1.45	0.00 - 25.57
逆ガンマ分布	0.94	0.10	0.00 - 6.93
一様分布	3.74	1.26	0.00 - 23.25

今回のシミュレーション設定においては、平均値と中央値は半コーシー分布と一様分布とで近い結果になりました。一方、逆ガンマ分布に関しては分布の中心が非常に小さな値になっていることもわかります。

まとめ

ランダム効果モデルにおける分散パラメータに関して、Gelman(2006)にて事前分布として提案された「半コーシー分布」を用いる場合のギブス・サンプリングについて説明し、Rでの実装例とシミュレーション実験結果を紹介しました。
今回行った実験では、半コーシー分布と一様分布での推定結果は少なくとも要約統計量に関して言えばあまり違いはなく、半コーシー分布を用いることによる劇的な効果を示すことはできませんでした。しかしながら、半コーシー分布を用いるメリットはいろいろな所で言われており、選択肢の一つとして理解しておくと良いように思いました。

参考文献

[1] Gelman, A. (2006). Prior distributions for variance parameters in hierarchical models (comment on article by Browne and Draper). Bayesian analysis, 1(3), 515-534.
[2] 松浦健太郎(2016). StanとRでベイズ統計モデリング. 共立出版.
[3] Half-Cauchy distribution — Probability Distribution Explorer documentation
[4] Cauchy distribution - Wikipedia

*1:Gelman論文ではより一般の「半t分布」について取り上げられていますが、本記事では話を簡単にするために半コーシー分布のみを扱います。なお、t分布の自由度を1にしたものがコーシー分布です。

*2:前述の通り、位置を表すパラメータは0としています。

*3:Gelman論文の本文では、正規分布の分散を1にして、逆ガンマ分布のパラメータによって半コーシー分布のスケールパラメータを調節するような説明がされていますが、個人的には論文付録のコード例に記載の方法（逆ガンマ分布のパラメータをに固定し、正規分布の標準偏差でスケールパラメータを定義する）がわかりやすかったので、以降の導出もそちらで進めています。

*4:厳密な説明ではないかもしれませんが、先はまだ長いのでこの程度でご容赦ください。

*5:サンプリングの初期値設定なども半コーシー分布の場合に揃えています。したがって、前回の記事とは結果が異なっています。

ギブス・サンプリングの実装練習：(1-2)分散成分の事前分布を一様分布にする

はじめに

今回は、以前の記事「ギブス・サンプリングの実装練習：(1)ランダム効果モデル」の続編です。
mstour.hatenablog.com

この記事で紹介したギブス・サンプリングでは、ランダム効果の分散の事後分布の推定がどうもうまくいっていないようでした。
理由の一つとして考えられるのは、分散の事前分布として逆ガンマ分布を選択していることです。
逆ガンマ分布は「条件付き共役」という数学的に便利な性質があるため古くから用いられる機会が多く、前回題材にしたGelfandらの論文（参考文献[1]）でもこれを用いたベイズモデルが示されています。特に「無情報」であることを反映するために、2つのパラメータをそれぞれある小さな値に設定した逆ガンマ分布がしばしば用いられます。
しかし、Gelmanの2006年の論文（参考文献[2]）では、逆ガンマ分布を用いたときの事後分布の推定結果はパラメータの設定に大きく影響されうることが述べられています。特に分散が小さめの値を取りうるような場合にはその影響が強くなります*1。

Gelman論文では事前分布の設定についていくつかの提案がなされていますが、今回はその中の一つである一様分布を用いた場合のギブス・サンプリングアルゴリズムを説明します。またRによる実装例と計算結果も紹介します。

用いるモデル（再掲）

今回も、Gelfand論文に登場した以下のランダム効果モデルを用いることにします。

なお、で、パラメータを与えたもとでは全て互いに独立であるとします。
またの事前分布は前回と同様の正規分布を設定しますが、分散成分についてはではなく、それらの平方根、つまり標準偏差の事前分布に一様分布を設定することにします*2。なおで、0からAの範囲の一様分布を表すものとします。

さて、まずは今回もギブス・サンプリングに必要となる未知パラメータの完全条件付き分布を導出していきます。
ただし、分散成分に関しては、サンプリングの対象を標準偏差ではなく分散とします。これは分散の完全条件付き分布が前回と同様に逆ガンマ分布で表せるためです*3。
そのためには、変数変換の公式を用いて分散の事前分布を導出しておく必要があります。
一般に、確率分布をもつ変数を2乗した変数の確率分布は

と表されます。この変換公式を用いるとのときとなるので、これを利用して完全条件付き分布を計算することにします。

なお、サンプリングアルゴリズムは前回と同じく完全条件付き分布から順番にサンプリングを繰り返す手順なので、今回は記載を省略します。

完全条件付き分布

の完全条件付き分布

以下のように変形できます（記号は、左辺と右辺が比例している、つまり左辺は右辺に定数を掛け算したものであることを表します）。
なお、途中の式変形の細かな理屈についてはよろしければ前回の記事をご参照ください。

最後の行の式の形から、完全条件付き分布は2つのパラメータをもつ逆ガンマ分布であることがわかります。

の完全条件付き分布

同様にして以下のように変形できます。

最後の結果から、完全条件付き分布はパラメータをもつ逆ガンマ分布となります。

の完全条件付き分布

については分散成分の事前分布は計算に関わってこないので、完全条件付き分布は前回と同じくになります。

の完全条件付き分布

についても同様に、前回と同じく
共分散行列：
平均：
をもつ多変量正規分布になります。

Rコードと結果

今回の設定にてギブス・サンプリングを実行するためのRコードの例を以下に示します。
データの生成やMCMCの設定に関するコードは前回のものを踏襲しています。

library(tidyverse)
library(MASS)
library(MCMCpack)

set.seed(819)

#----- sample data -----
K = 6
J = 5
mu = 5
s2_theta = 4
s2_e = 16

theta = rnorm(K, mean = mu, sd = sqrt(s2_theta))
e = rnorm(K*J, mean = 0, sd = sqrt(s2_e))
Y = rep(theta, each = J) + e
Ymat = matrix(Y, nrow = K, ncol = J, byrow = T)
Ybar = apply(Ymat, 1, mean)


#----- Gibbs sampling -----
# MCMC設定
nsamp = 11000
burnin = 1000
thin = seq(burnin+1, nsamp, by = 1)

# hyperparameter
mu_0 = 0
s2_0 = 10000

# 結果の入れ物
s2_theta_s = array(NA, length(thin))
s2_e_s = array(NA, length(thin))
mu_s = array(NA, length(thin))
theta_s = array(NA, c(K, length(thin)))

# Gibbs sampling初期値
s2_theta_g = runif(1)
s2_e_g = runif(1)
mu_g = runif(1)
theta_g = rep(runif(1), K)

### sampling
for(s in 1:nsamp){
  if((round(s/500) - (s/500)) == 0){print(s)}
  # s2_theta
  a = -1/2 + K/2
  b = sum((theta_g - rep(mu_g, K))^2)/2
  s2_theta_g = rinvgamma(1, a, b) # MCMCpack
  s2_theta_s[s==thin] = s2_theta_g
  
  # s2_e
  a = -1/2 + (K*J)/2
  b = sum((Y - rep(theta_g, each = J))^2)/2
  s2_e_g = rinvgamma(1, a, b)
  s2_e_s[s==thin] = s2_e_g
  
  # mu
  a = (s2_theta_g * mu_0 + s2_0 * sum(theta_g)) / (s2_theta_g + K * s2_0)
  b = (s2_theta_g * s2_0) / (s2_theta_g + K * s2_0)
  mu_g = rnorm(1, mean = a, sd = sqrt(b))
  mu_s[s==thin] = mu_g
  
  # theta
  coef1 = (J * s2_theta_g) / (J * s2_theta_g + s2_e_g)
  coef2 = (s2_e_g) / (J * s2_theta_g + s2_e_g)
  coef3 = (s2_theta_g * s2_e_g) / (J * s2_theta_g + s2_e_g)
  a = coef1 * Ybar + coef2 * rep(mu_g, K)
  b = diag(rep(coef3, K))
  theta_g = mvrnorm(1, mu = a, Sigma = b)
  theta_s[, s==thin] = theta_g
}

#----- Results -----
# mu
val = mu_s
summary(mu_s)

mu_df = as.data.frame(val) %>%
  mutate(Iter = 1:length(thin))
ggplot(mu_df, aes(x = Iter, y = val)) + geom_line() +
  geom_hline(yintercept = mu, color = "red") +
  geom_hline(yintercept = median(mu_df$val), color = "blue") +
  labs(y = "mu") + theme_bw()

# s2_theta
val = s2_theta_s
summary(s2_theta_s)

s2_theta_df = as.data.frame(val) %>%
  mutate(Iter = 1:length(thin))
ggplot(s2_theta_df, aes(x = Iter, y = val)) + geom_line() +
  geom_hline(yintercept = s2_theta, color = "red") +
  geom_hline(yintercept = median(s2_theta_df$val), color = "blue") +
  ylim(c(0, 20)) +
  labs(y = "sigma^2_theta") + theme_bw()

# s2_e
val = s2_e_s
summary(s2_e_s)

s2_e_df = as.data.frame(val) %>%
  mutate(Iter = 1:length(thin))
ggplot(s2_e_df, aes(x = Iter, y = val)) + geom_line() +
  geom_hline(yintercept = s2_e, color = "red") +
  geom_hline(yintercept = median(s2_e_df$val), color = "blue") +
  labs(y = "sigma^2_e") + theme_bw()

得られた事後分布サンプルの要約統計量とトレースプロットは次のようになりました（トレースプロットは、の順番です）。
なおのトレースプロットについて前回書き忘れていたのですが、時々あまりにも大きな値がサンプリングされるので、図示する範囲を0から20の間に制限していました。今回も同様にしています。

前回の設定（事前分布に逆ガンマ分布を設定）ではのサンプルの中央値はほぼ0となっていましたが、今回は1.27であり、真の値により近い結果になりました（トレースプロットでは真の値を赤線、中央値を青線で表示しています）。一方、については、前回と同様におおむね真の値（赤線）の近辺にサンプルが分布しています。

ところで前回も同様ですが、シミュレーションデータでは個人の数をJ=6、個人ごとの測定数をK=5としていました。特にランダム効果（個人差）のばらつきを推定するための情報は6個しかないことになるため、をうまく推定するのは少し難しいのかもしれません。
補足として、J、Kをそれぞれ20に増やした時の結果を以下に掲載します。

J=6、K=5の場合と比べて、のサンプルはより真の値の近くに分布するようになり、サンプル間のばらつきも小さくなっているのが確認できるかと思います。

なお、逆ガンマ分布の設定でJ、Kを20にしたときの結果は次のようになりました。

データの数が増えると、逆ガンマ分布を設定した場合も一様分布の場合と同じような推定結果が得られました。

まとめ

前回はシンプルなランダム効果モデルについて、分散の事前分布に逆ガンマ分布を設定した場合のギブス・サンプリングを紹介しましたが、今回は分散の平方根（標準偏差）の事前分布を一様分布にした場合の手順と結果を示しました。
Gelman論文で述べられているように、データ数が少ないと逆ガンマ分布を設定した時の推定精度があまり良くなく、一様分布に設定することで改善されるという結果になりました。ただ、データ数が多くなれば、少なくとも今回のシミュレーション設定においては結果はあまり変わらないようでした。
さて、分散成分の事前分布としては比較的よく使用されるものが他にもあります。このシリーズの最後にそれを紹介できればと思います。

参考文献

[1] Gelfand, A. E., Hills, S. E., Racine-Poon, A., & Smith, A. F. (1990). Illustration of Bayesian inference in normal data models using Gibbs sampling. Journal of the American Statistical Association, 85(412), 972-985.
[2] Gelman, A. (2006). Prior distributions for variance parameters in hierarchical models (comment on article by Browne and Draper). Bayesian analysis, 1(3), 515-534.
[3] 松浦健太郎(2016). StanとRでベイズ統計モデリング. 共立出版.

*1:ざっくり言うと、逆ガンマ分布のパラメータの値を小さくすると、小さな値の部分に確率密度が集中した形状の分布になるため、事後分布が事前分布の影響を強く受けてしまうのが理由のようです。

*2:もちろん分散が一様分布に従うとしてもよいのですが、Gelman論文では推奨しないと述べられているため今回もそれに従いました。また同論文ではランダム効果の分散成分に議論の的を絞っていますが、今回は誤差の分散成分も同様に一様分布としました。

*3:標準偏差の完全条件付き分布を計算してみましたが、どうもよく知られた確率分布では表せないような感じでした。メトロポリス・ヘイスティングス法などを使えばサンプリングできるのだと思いますが、よくわからなかったので今回はやめました・・・

ギブス・サンプリングの実装練習：(1)ランダム効果モデル

2021/11/14 赤字部分を追記

はじめに

このブログではあまりベイズ統計の話題は書いてこなかったのですが、やはりこれからの時代それではいかんということで、こんなことをやってみることにします。

ベイズモデルにおいてパラメータの事後分布を推定する際にはMCMC法がよく使われますが、代表的なアルゴリズムの一つにギブス・サンプリング(Gibbs sampling)というものがあります。
この方法はざっくり言うと、推定したいパラメータ一つ一つの「完全条件付き分布(Full conditional distribution)」*1を導出し、そこから順繰りにサンプリングを繰り返せば各パラメータの事後分布の推定ができる、というものです。

今回はギブス・サンプリングの理論的な説明ではなく、具体的な計算をRで実行するためのコードを書いてみることにします。
今回の題材は、Gelfandらの1990年の論文（参考文献[1]）にて解説されている以下のランダム効果モデルです。

ただしは互いに独立に正規分布に、は互いに独立に正規分布に従うものとし、どうしも互いに独立とします。
ここでは、はそれぞれ個人の番目の測定値とランダムな誤差を表すものとし、は個人に特有の個人差を表すランダム効果と考えます*2。

またパラメータは互いに独立に以下の事前分布に従うものとします（は「逆ガンマ分布」を表します）：

ただし、上記の事前分布のパラメータ（ハイパーパラメータと言います）は全て既知の値とします*3。
これらは共役事前分布と呼ばれており、このように設定することで各パラメータの事後分布*4は事前分布と同じ種類の分布になることが知られています。したがって手計算によって事後分布を具体的に導出することができます。
もちろん実用では共役事前分布を用いる必要はないのですが（むしろ現実に即したモデリングには適さないことがあるかもしれません）、事後分布が基本的な確率分布で書き下せるため、今回やろうとしているギブス・サンプリングには非常に都合が良いわけです。

さて、データが得られたと想定して、パラメータの事後分布の推定をギブス・サンプリングを用いて行ってみたいと思います。
サンプリングを行うためには、パラメータの他に、ランダム効果の完全条件付き分布の特定が必要です。
まずはこれらの完全条件付き分布を導出し、それを用いたサンプリングアルゴリズムを示します。
その後、Rでの実装例と結果を紹介していきます。

完全条件付き分布の導出

今回の例では、の完全条件付き分布は全てよく知られた確率分布になることを手計算で確かめることができます。少し大変ですが、一つずつやっていきます。

の完全条件付き分布

まずはの完全条件付き分布、つまり他の変数で条件付けた分布を導出します。なお、得られたデータを反映した事後分布を推定するためには、での条件付けも必要です。
条件付き確率の定義を用いると、次のように変形できます。なお記号は左辺と右辺が比例関係にあることを表します*5。

最後の式変形には少し注意が必要です。を条件付き確率の定義にしたがって変形してみます。

なお最後の等式に移る際に、条件部分にある無関係なパラメータを削除しました。
モデルの設定から、の値は、分布の平均パラメータと分散パラメータの両方に依存します。したがって、分子のと分母のが必ずしも一致しないため、完全条件付き分布にはの2つの確率分布が残ることになります。もしもがに依存しない構造になっていれば、残るのはだけになります。

さて、完全条件付き分布は3つの確率分布の積の形になっていることがわかりましたが、モデルの設定より、これらは全て正規分布です。この時、最終的に得られる分布も正規分布になります。
具体的に式を変形していくと、以下のようになります。

確率分布を上記のような2次式の指数関数の形で表すことができるとき、その確率分布は正規分布であることが知られており、平均と分散はそれぞれ1次および2次の項の係数を使って表せます。高校の時？に学んだようにの係数をくくり出して整理すれば、正規分布でよく見慣れた形になるのが確かめられます。
結果、完全条件付き分布はとなります。

の完全条件付き分布

同様にして数式展開していきましょう。
の事前分布はパラメータの逆ガンマ分布としていました。

最後の等式の形から、完全条件付き分布はパラメータの逆ガンマ分布であることがわかります。

の完全条件付き分布

の時とほぼ同様です。

よって、パラメータの逆ガンマ分布になります。

の完全条件付き分布

最後に、をまとめたベクトルの多変量分布を導出します。
こちらはベクトル演算が入るので少しややこしくなります。

ただし、としました。または1を並べたベクトル、はベクトルの転置です。
最後の形から、この分布は多変量正規分布になることが知られています。なおとに挟まれた行列の逆行列が共分散行列、の右部分にあるベクトルに左から共分散行列を掛けたものが平均ベクトルになります。整理すると
共分散行列：
平均：

のようになります。

今回のギブス・サンプリングでは、以上の4つの完全条件付き分布から所定の回数サンプリングを繰り返します。まとめると以下の手順になります（サンプリングの順番は論文に合わせました）。

1. の初期値を適当に決める。
2. からをサンプリングする。ただし他のパラメータは一つ前のステップの値を用いる（以降も同様）。
3. からをサンプリング。
4. からをサンプリング。
5. からをサンプリング。
6. 以降、2〜5を所定の回数繰り返す。

Rでの実装

では、これをRで実際に計算するプログラムを作っていきましょう。
まずはサンプルデータを作成します。今回は、次のようなモデルからデータが生成されるものとします。

準備も含め、データ生成には以下のコードを用いました。

library(tidyverse)
library(MASS)
library(MCMCpack)

set.seed(819)

K = 6
J = 5
mu = 5
s2_theta = 4
s2_e = 16

theta = rnorm(K, mean = mu, sd = sqrt(s2_theta))
e = rnorm(K*J, mean = 0, sd = sqrt(s2_e))
Y = rep(theta, each = J) + e
Ymat = matrix(Y, nrow = K, ncol = J, byrow = T)
Ybar = apply(Ymat, 1, mean)

生成された測定値データは次のようになります。

モデルのパラメータにはそれぞれという値を設定しています。これらの事後分布が今回の推定対象です。
また各パラメータには「はじめに」で述べたような事前分布を設定しますが、ハイパーパラメータの値は既知としているので、具体的な値を与えます。

サンプリングの準備として次のような設定を行います。

# MCMC設定
nsamp = 11000
burnin = 1000
thin = seq(burnin+1, nsamp, by = 1)

# hyperparameter
mu_0 = 0
s2_0 = 10000
a_1 = 0.001
b_1 = 0.001
a_2 = 0.001
b_2 = 0.001

# 結果の入れ物
s2_theta_s = array(NA, length(thin))
s2_e_s = array(NA, length(thin))
mu_s = array(NA, length(thin))
theta_s = array(NA, c(K, length(thin)))

# Gibbs sampling初期値
s2_theta_g = runif(1)
s2_e_g = runif(1)
mu_g = runif(1)
theta_g = rep(runif(1), K)

• MCMC設定：11000回のサンプリングを行い、そのうち最初の1000回は推定に使用せず捨てることとしています。また、サンプルの間引き(thinning)を行うことを意図したコード（"thin"で定義）にしていますが、今回は間引きは行いませんでした（by=1としています）。
• hyperparameter：前述の事前分布のハイパーパラメータです。
• 結果の入れ物：得られたサンプルを格納するオブジェクトです。ギブス・サンプリングのステップにはのサンプリングも含むため、これらのサンプルも格納する必要があります。
• Gibbs sampling初期値：前の時点で得られたサンプルの値を計算に使用するので、始まりの値を何らか与えなければなりません。今回は0〜1の間の値のランダムサンプルを用いることにしました。

以下のようなコードで、前半で導出した各パラメータの完全条件付き分布から順繰りにサンプリングを繰り返していきます。逆ガンマ分布のサンプリングに用いた"rinvgamma"関数はパッケージ"MCMCpack"にあります。

### sampling
for(s in 1:nsamp){
  if((round(s/500) - (s/500)) == 0){print(s)}
  # s2_theta
  a = a_1 + K/2
  b = b_1 + sum((theta_g - mu_g)^2)/2
  s2_theta_g = rinvgamma(1, a, b) # MCMCpack
  s2_theta_s[s==thin] = s2_theta_g
  
  # s2_e
  a = a_2 + (K*J)/2
  b = b_2 + sum((Y - rep(theta_g, each = J))^2)/2
  s2_e_g = rinvgamma(1, a, b)
  s2_e_s[s==thin] = s2_e_g
  
  # mu
  a = (s2_theta_g*mu_0 + s2_0*sum(theta_g))/(s2_theta_g + K*s2_0)
  b = (s2_theta_g*s2_0)/(s2_theta_g + K*s2_0)
  mu_g = rnorm(1, mean = a, sd = sqrt(b))
  mu_s[s==thin] = mu_g
  
  # theta
  coef1 = (J*s2_theta_g)/(J*s2_theta_g + s2_e_g)
  coef2 = (s2_e_g)/(J*s2_theta_g + s2_e_g)
  coef3 = (s2_theta_g*s2_e_g)/(J*s2_theta_g + s2_e_g)
  a = coef1 * Ybar + coef2 * rep(mu_g, K)
  b = diag(rep(coef3, K))
  theta_g = mvrnorm(1, mu = a, Sigma = b)
  theta_s[, s==thin] = theta_g
}

推定結果を確認するため、サンプルの要約統計量とトレースプロットを以下のコードで出力しました。
トレースプロットをggplot2で作成するため、サンプルをデータフレームに変換しています。

# 要約統計量
summary(mu_s)
summary(s2_theta_s)
summary(s2_e_s)

# サンプルのトレースプロット
# mu
val = mu_s
mu_df = as.data.frame(val) %>%
  mutate(Iter = 1:length(thin))

ggplot(mu_df, aes(x = Iter, y = val)) + geom_line() +
  geom_hline(yintercept = mu, color = "red") +
  geom_hline(yintercept = median(mu_df$val), color = "blue") +
  labs(y = "mu") + theme_bw()

# s2_theta
val = s2_theta_s
s2_theta_df = as.data.frame(val) %>%
  mutate(Iter = 1:length(thin))

ggplot(s2_theta_df, aes(x = Iter, y = val)) + geom_line() +
  geom_hline(yintercept = s2_theta, color = "red") +
  geom_hline(yintercept = median(s2_theta_df$val), color = "blue") +
  ylim(c(0, 20)) +
  labs(y = "sigma^2_theta") + theme_bw()

# s2_e
val = s2_e_s
s2_e_df = as.data.frame(val) %>%
  mutate(Iter = 1:length(thin))

ggplot(s2_e_df, aes(x = Iter, y = val)) + geom_line() +
  geom_hline(yintercept = s2_e, color = "red") +
  geom_hline(yintercept = median(s2_e_df$val), color = "blue") +
  labs(y = "sigma^2_e") + theme_bw()

計算結果

トレースプロットは以下のようになりました。上から順に、です。真の値を赤線、サンプルの中央値を青線で示しました。
ただしは時々非常に大きい値がサンプリングされているため、真の値近辺の結果を確認できるようプロットの範囲を0から20に制限しています。

はおおむね真の値の周辺に分布しているようですが、は多くのサンプルが0の近辺にある一方、時々大きな値も生成されています。
題材の論文でもこのような結果になっており、さらに事前分布の設定によっても分布の形状が変わるようです。
今回は長くなるのでアルゴリズムの紹介程度にとどめたいのですが、また別の機会にもう少し今回の結果を掘り下げて考えてみたいと思います。
なお、サンプルの要約統計量は以下のようになりました。

おわりに

今回はMCMCのアルゴリズムの一つ、ギブス・サンプリングをRで実施するためのコード作成例を紹介しました。
正しく数式展開をすることに加えて、ソフトウェアのコーディングが間違っていないかも注意深く確かめなくてはならないため、自分で実装するのは正直言ってかなり骨が折れます。
また気力がある時に続編を書ければいいなと思います・・・

参考文献

[1] Gelfand, A. E., Hills, S. E., Racine-Poon, A., & Smith, A. F. (1990). Illustration of Bayesian inference in normal data models using Gibbs sampling. Journal of the American Statistical Association, 85(412), 972-985.

*1:モデルに含まれる他の全部の確率変数で条件付けした確率分布のことです。ギブス・サンプリングを行うには、通常、条件付けした場合の確率分布を数式で書き起こす必要があります。

*2:他の例として、集団における個人から得られたデータをこのモデルで表現することもできます。

*3:ハイパーパラメータにも事前分布を設定することができますが、今回は具体的な数値を与えることにしています。

*4:厳密には、今回は「他のパラメータで条件つけた」事後分布のことを指します。一方、ややこしいですが、サンプリングによって得られた分布は各パラメータの「完全条件付き」ではない事後分布になります。

*5:このような表現を用いることで、関心あるパラメータに関係のない定数を省略して話を進めることができます。

欠測データ分析シミュレーションのための実戦練習：(2)反復測定データの欠測（最終時点のみ）

はじめに

今回は、以前の記事でご紹介したシミュレーションプログラム作成練習の続きをやっていきたいと思います。
mstour.hatenablog.com

題材は、第1回と同様こちらの論文で実施されたシミュレーション研究です。
www.ncbi.nlm.nih.gov

前回は1つのアウトカム変数だけが欠測する状況を扱ったのですが、アウトカム変数が同じ個人から繰り返し測定される状況を考えたいこともあります。少し難易度が上がりますが、現実の場面では役に立つことがあるかと思います。
今回は、アウトカム変数が同じ個人から2回測定され、関心のある最後の測定値が欠測する場合を考えてみます。

データ

今回も、対照治療に対する試験治療の効果を評価するランダム化比較試験を想定します。
まずは完全データの作成手順について、Rコードとともに説明します。

被験者数は2つのグループ（一方は試験治療を、他方は対照治療を受けます）合わせて600人で、ランダム化前に測定された連続型ベースライン変数の1つである*1がアウトカムに影響するという状況を想定します*2。またグループを示す変数をとします。
まず、とを発生させます。は前回と同様、標準正規分布に従うものとします*3。

n = 600
T = c(rep(1, n/2), rep(0, n/2))
X = rnorm(n, mean = 0, sd = 1)

次に、アウトカム変数のうち1回目に測定されたものを、2回目に測定されたものをとします。同じ個人から測定される値どうしの相関を考慮するため、は多変量正規分布からサンプリングします。
また、の平均はそれぞれ治療グループごと、ベースライン変数の値ごとに異なるものとします*4。
今回のシミュレーションでは、具体的には以下のように設定します。

アウトカム変数どうしの相関は、0.3と0.7の2パターンの設定を考えることにします。
今回は次のようなコードで作成してみます。
まずは平均0・分散1で、相関が0.3（または0.7）の2変量正規分布からのサンプリングを行います。

# mvrnorm関数を使うため、MASSを読み込みます
library(MASS)

s_z = 1
s_y = 1

# 相関0.3の場合
s_zy_1 = 0.3
cov_zy_1 = matrix(c(s_z, s_zy_1, s_zy_1, s_y), nrow = 2)
e_zy_1 = mvrnorm(n, c(0, 0), cov_zy_1)

# 相関0.7の場合
s_zy_2 = 0.7
cov_zy_2 = matrix(c(s_z, s_zy_2, s_zy_2, s_y), nrow = 2)
e_zy_2 = mvrnorm(n, c(0, 0), cov_zy_2)

続いて、最初に発生させたを用いて平均を定義し、上記で発生させたサンプルに加えることでを得ます。

alpha1 = 0.3
alpha2 = 0.3
beta1 = 0.3
beta2 = 0.3

# 相関0.3の場合
Z_1 = alpha1 * T + alpha2 * X + e_zy_1[, 1]
Y_1 = beta1 * T + beta2 * X + e_zy_1[, 2]
cd_1 = data.frame(ID = 1:n, T = T, X = X, Z = Z_1, Y = Y_1)

# 相関0.7の場合
Z_2 = alpha1 * T + alpha2 * X + e_zy_2[, 1]
Y_2 = beta1 * T + beta2 * X + e_zy_2[, 2]
cd_2 = data.frame(ID = 1:n, T = T, X = X, Z = Z_2, Y = Y_2)

このような完全データができあがります。

発生させた完全データのうち、今回はのみが欠測するものとします。
欠測メカニズムはMissing At Random(MAR)とし、欠測確率に関係する変数は前の時点におけるアウトカム変数であるだけという設定にします。の影響度は「値が1標準偏差大きくなるごとに欠測のオッズが2.5倍になる」ものとし、欠測するデータの割合は50%とします。

よって、各個人のの欠測確率は次のように定義できます：

切片の-0.375は、前回と同様、に平均値を、に0.5を代入して算出した値です。今回もこの設定で欠測データの割合が50%近くなることを確認しました。

欠測を発生させるコード例は以下の通りです。ここではtidyverseパッケージを使っていますので、事前に読み込んでおく必要があります。

library(tidyverse)

b = -0.375

# 相関0.3の場合
missp_1 = 1 / (1 + exp( - (b + 2.5 * Z_1)))
unif_1 = runif(n, min = 0, max = 1)
md_1 = cd_1 %>%
  mutate(missp = missp_1, unif = unif_1) %>%
  mutate(missfl = case_when(missp > unif ~ 1, TRUE ~ 0), Y_miss = case_when(missfl == 0 ~ Y))

# 相関0.7の場合
missp_2 = 1 / (1 + exp( - (b + 2.5 * Z_2)))
unif_2 = runif(n, min = 0, max = 1)
md_2 = cd_2 %>%
  mutate(missp = missp_2, unif = unif_2) %>%
  mutate(missfl = case_when(missp > unif ~ 1, TRUE ~ 0), Y_miss = case_when(missfl == 0 ~ Y))

以下のデータの変数「Y_miss」が、のうち一部を欠測させたものです。

分析

作成した欠測データに対して、今回は以下の3種類の分析を行います。
推定するのはアウトカムの2グループ間における平均的な差（治療効果）です。の平均はなので、推定結果が0.3に近ければ*5適切な分析方法だと考えてよいでしょう。

(1) 欠測を無視した分析（CCA; Complete Case Analysis）
欠測のないレコードのみを使用し、を目的変数、とを説明変数とする線形モデルをあてはめます。
以下のようなRコードを用いました。

# モデルあてはめ
mod_2_1 = lm(Y_miss ~ T + X, data = md_2)
# 推定値の抽出
mod_2_1$coefficients["T"]

線形モデルにおけるの回帰係数がグループ間のアウトカムの差に相当するので、モデルのあてはめ結果から抽出します。

(2) 多重代入法（MI; Multiple Imputation）
欠測しているを多重代入法により補完した上で、のグループ間の単純比較を行います（を目的変数、のみを説明変数とする線形モデル）。
を補完するモデルの説明変数には、の値そのものに影響すると、また欠測確率に影響するを使用します。
Rコードは前回とほぼ同様です。

library(mice)

# 補完モデルを行列形式で設定
pm_2_2 = matrix(c(rep(0, 9), rep(0, 9), rep(0, 9), rep(0, 9),
                  rep(0, 9), rep(0, 9), rep(0, 9), rep(0, 9),
                  0, 1, 1, 1, 0, 0, 0, 0, 0), nrow = 9, byrow = T)
# MICEにより補完
imp_2_2 = mice(data = md_2, m = 50, method = "norm", predictorMatrix = pm_2_2)
# 各補完データセットにおけるモデルあてはめ
mod_2_2_0 = with(imp_2_2, lm(Y_miss ~ T))
# 推定結果の統合
mod_2_2 = pool(mod_2_2_0)
# 統合した推定結果を抽出
summary(mod_2_2)[2, "estimate"]

(3) 線形混合モデル（Linear Mixed Model）
反復測定データの分析によく用いられる方法で、欠測がある場合にも（ある条件が満たされていれば）正しい推定を行えることが知られています。（以前書いた説明はこちら）
(2)のようなデータの補完はせずに欠測のないレコードのみ使用しますが、(1)と異なり反復測定されたアウトカム変数全て（今回はおよび）を目的変数とします。
説明変数はのほか、測定時点（1、2）を示す情報も含めます。またグループと測定時点との交互作用項も含めることにします*6。

題材の論文では、アウトカム変数の誤差項の共分散行列は「unstructured covariance matrix」とし、自由度の推定にはKenward-Roger法を用いた、との記載があります。
（共分散行列についてはこちらの記事で、Kenward-Roger法についてはこちらの記事でそれぞれ紹介しました。）
しかしながら、Rでは現時点ではunstructured covariance matrixとKenward-Roger法を合わせて使用する方法がないようです（参考文献[2]）。
今回のシミュレーションでは自由度計算を使う必要はないので、unstructured covariance matrixの指定のみ行うことにします。参考文献[2]に倣い、nlmeパッケージのgls関数を使用します。
そのために、まずは反復測定データを横並びの状態から縦型データへ加工します。R以外の統計ソフトウェアでも、混合モデルを用いる際はこの形のデータを必要とすることがよくあります。

# データセットmd_2を縦型に変更
md_2_l = md_2 %>%
  dplyr::select(-Y, -missp, -unif, -missfl) %>%
  tidyr::pivot_longer(cols = c(Z, Y_miss), names_to = "VARS", values_to = "VAL") %>%
  dplyr::mutate(TIME = case_when(VARS == "Z" ~ 1, VARS == "Y_miss" ~ 2))

最初にdplyr::selectで不要な変数を削除し、次にtidyr::pivot_longerで横型のデータセットを縦型に変更しています。cols = で縦に並べる変数を指定します。names_to = で縦型に変更した元の変数名を格納する変数の名称、values_to = で縦型に変更した値を格納する変数の名称をそれぞれ決めることができます。
最後にdplyr::mutateで時点を示す変数を作りました。
縦型に加工した後のデータは次のようになります。

混合モデルはgls関数で次のように実行できます。

library(nlme)

# 誤差項の共分散行列をunstructuredとするLinear mixed modelのあてはめ
mod_2_3 = gls(VAL ~ T + X + factor(TIME) + T*factor(TIME), data = md_2_l, na.action = na.omit,
              correlation = corSymm(form = ~ TIME | ID), weights = varIdent(form = ~ 1 | TIME))
# 推定結果の抽出（時点2の結果を見るため、交互作用項の係数を足す）
mod_2_3$coefficients["T"] + mod_2_3$coefficients["T:factor(TIME)2"]

上記のコードでは、correlation = の部分で共分散行列の非対角成分、weights = の部分で対角成分をそれぞれ設定しています。またna.action = na.omit と指定することで、欠測のある個人が分析対象から除外されてしまわないようにしています*7。

今回のシミュレーションでも、以上の一連の流れを所定の回数反復し、推定値の平均と標準偏差をプロットすることにしました。
コード全体は次項にまとめています（作図のコードもこちらに掲載しています）。

シミュレーションコードまとめ

library(tidyverse)
library(mice)
library(MASS)
library(nlme)

set.seed(1815)

#----- simulation -----
### parameter setting
nsim = 2000

n = 600
alpha1 = 0.3
alpha2 = 0.3
beta1 = 0.3
beta2 = 0.3
s_z = 1
s_y = 1
s_zy_1 = 0.3
s_zy_2 = 0.7
cov_zy_1 = matrix(c(s_z, s_zy_1, s_zy_1, s_y), nrow = 2)
cov_zy_2 = matrix(c(s_z, s_zy_2, s_zy_2, s_y), nrow = 2)
b = -0.375

### corr=0.3
result_1_1 = NULL
result_1_2 = NULL
result_1_3 = NULL
for (i in 1:nsim){
  # data
  T = c(rep(1, n/2), rep(0, n/2))
  X = rnorm(n, mean = 0, sd = 1)
  e_zy_1 = mvrnorm(n, c(0, 0), cov_zy_1)
  Z_1 = alpha1 * T + alpha2 * X + e_zy_1[, 1]
  Y_1 = beta1 * T + beta2 * X + e_zy_1[, 2]
  cd_1 = data.frame(ID = 1:n, T = T, X = X, Z = Z_1, Y = Y_1)
  missp_1 = 1 / (1 + exp( - (b + 2.5 * Z_1)))
  unif_1 = runif(n, min = 0, max = 1)
  md_1 = cd_1 %>%
    mutate(missp = missp_1, unif = unif_1) %>%
    mutate(missfl = case_when(missp > unif ~ 1, TRUE ~ 0),
           Y_miss = case_when(missfl == 0 ~ Y))
  ### analysis
  # cca
  mod_1_1 = lm(Y_miss ~ T + X, data = md_1)
  result_1_1 = rbind(result_1_1, mod_1_1$coefficients["T"])
  # mi overall
  pm_1_2 = matrix(c(rep(0, 9), rep(0, 9), rep(0, 9), rep(0, 9),
                    rep(0, 9), rep(0, 9), rep(0, 9), rep(0, 9),
                    0, 1, 1, 1, 0, 0, 0, 0, 0), nrow = 9, byrow = T)
  imp_1_2 = mice(data = md_1, m = 50, method = "norm", predictorMatrix = pm_1_2)
  mod_1_2_0 = with(imp_1_2, lm(Y_miss ~ T))
  mod_1_2 = pool(mod_1_2_0)
  result_1_2 = rbind(result_1_2, summary(mod_1_2)[2, "estimate"])
  # linear mixed model
  md_1_l = md_1 %>%
    dplyr::select(-Y, -missp, -unif, -missfl) %>%
    tidyr::pivot_longer(cols = c(Z, Y_miss), names_to = "VARS", values_to = "VAL") %>%
    dplyr::mutate(TIME = case_when(VARS == "Z" ~ 1, VARS == "Y_miss" ~ 2))
  mod_1_3 = gls(VAL ~ T + X + factor(TIME) + T*factor(TIME),
                data = md_1_l, na.action = na.omit,
                correlation = corSymm(form = ~ TIME | ID),
                weights = varIdent(form = ~ 1 | TIME))
  tmp = mod_1_3$coefficients["T"] + mod_1_3$coefficients["T:factor(TIME)2"]
  result_1_3 = rbind(result_1_3, tmp)
}

mean_1 = c(mean(result_1_1), mean(result_1_2), mean(result_1_3))
sd_1 = c(sd(result_1_1), sd(result_1_2), sd(result_1_3))
summary_1 = data.frame(analysis = c("CCA", "MI overall m=50", "Linear mixed model"),
                       mean = mean_1, sd = sd_1)
ggplot(data = summary_1, aes(x = analysis, y = mean, color = analysis)) +
  geom_errorbar(aes(ymin = mean-sd, ymax = mean+sd), width = 0.1) +
  geom_point(size = 3) +
  geom_hline(yintercept = 0.3, linetype = 2, size = 0.3) +
  scale_y_continuous(breaks = c(0.2, 0.3, 0.4, 0.5), limits = c(0.10, 0.51)) +
  labs(title = "Corr(Y, Z) = 0.30", x = "", y = "Treatment effect estimate") +
  theme_classic()

### corr=0.7
result_2_1 = NULL
result_2_2 = NULL
result_2_3 = NULL
for (i in 1:nsim){
  # data
  T = c(rep(1, n/2), rep(0, n/2))
  X = rnorm(n, mean = 0, sd = 1)
  e_zy_2 = mvrnorm(n, c(0, 0), cov_zy_2)
  Z_2 = alpha1 * T + alpha2 * X + e_zy_2[, 1]
  Y_2 = beta1 * T + beta2 * X + e_zy_2[, 2]
  cd_2 = data.frame(ID = 1:n, T = T, X = X, Z = Z_2, Y = Y_2)
  missp_2 = 1 / (1 + exp( - (b + 2.5 * Z_2)))
  unif_2 = runif(n, min = 0, max = 1)
  md_2 = cd_2 %>%
    mutate(missp = missp_2, unif = unif_2) %>%
    mutate(missfl = case_when(missp > unif ~ 1, TRUE ~ 0),
           Y_miss = case_when(missfl == 0 ~ Y))
  ### analysis
  # cca
  mod_2_1 = lm(Y_miss ~ T + X, data = md_2)
  result_2_1 = rbind(result_2_1, mod_2_1$coefficients["T"])
  # mi overall
  pm_2_2 = matrix(c(rep(0, 9), rep(0, 9), rep(0, 9), rep(0, 9),
                    rep(0, 9), rep(0, 9), rep(0, 9), rep(0, 9),
                    0, 1, 1, 1, 0, 0, 0, 0, 0), nrow = 9, byrow = T)
  imp_2_2 = mice(data = md_2, m = 50, method = "norm", predictorMatrix = pm_2_2)
  mod_2_2_0 = with(imp_2_2, lm(Y_miss ~ T))
  mod_2_2 = pool(mod_2_2_0)
  result_2_2 = rbind(result_2_2, summary(mod_2_2)[2, "estimate"])
  # linear mixed model
  md_2_l = md_2 %>%
    dplyr::select(-Y, -missp, -unif, -missfl) %>%
    tidyr::pivot_longer(cols = c(Z, Y_miss), names_to = "VARS", values_to = "VAL") %>%
    dplyr::mutate(TIME = case_when(VARS == "Z" ~ 1, VARS == "Y_miss" ~ 2))
  mod_2_3 = gls(VAL ~ T + X + factor(TIME) + T*factor(TIME),
                data = md_2_l, na.action = na.omit,
                correlation = corSymm(form = ~ TIME | ID),
                weights = varIdent(form = ~ 1 | TIME))
  tmp = mod_2_3$coefficients["T"] + mod_2_3$coefficients["T:factor(TIME)2"]
  result_2_3 = rbind(result_2_3, tmp)
}

mean_2 = c(mean(result_2_1), mean(result_2_2), mean(result_2_3))
sd_2 = c(sd(result_2_1), sd(result_2_2), sd(result_2_3))
summary_2 = data.frame(analysis = c("CCA", "MI overall m=50", "Linear mixed model"),
                       mean = mean_2, sd = sd_2)
ggplot(data = summary_2, aes(x = analysis, y = mean, color = analysis)) +
  geom_errorbar(aes(ymin = mean-sd, ymax = mean+sd), width = 0.1) +
  geom_point(size = 3) +
  geom_hline(yintercept = 0.3, linetype = 2, size = 0.3) +
  scale_y_continuous(breaks = c(0.2, 0.3, 0.4, 0.5), limits = c(0.10, 0.51)) +
  labs(title = "Corr(Y, Z) = 0.70", x = "", y = "Treatment effect estimate") +
  theme_classic()

結果

今回も、治療効果（グループ間のアウトカムの差）の推定が平均的にどのようになるか、3つの分析方法それぞれの結果をプロットして確認します*8。

まず、アウトカム変数の時点間の相関を0.3とした場合です。

題材の論文の結果と同様に、多重代入法（青色）と混合モデル（緑色）はいずれも平均的に真の値0.3をほぼ正しく推定していますが、欠測を無視した分析（赤色）では少し小さめに評価してしまう傾向にありました。

相関が0.7の場合は以下のようになりました。

全シミュレーションを通した平均の値（丸印）は論文と少し異なる結果になりましたが、相関が0.3の場合と比べて欠測を無視したときの過小推定の程度が大きくなっている様子が再現できています。

おわりに

今回は同じ個人からアウトカム変数が2回測定されている反復測定データを考え、最終時点のみが欠測する場合の分析結果のシミュレーションを行いました。
現実には、もっと多くの測定回数があったり、複数時点で欠測が発生するような状況も多いかと思います。
それらも今回と同様の方法でシミュレーションすることができますが、せっかくなので次回以降に実施してみます。題材の論文ではこのようなケースは取り扱われていなかったので、次はお手本なしでいきます。

参考文献

[1] Sullivan, T. R., White, I. R., Salter, A. B., Ryan, P., & Lee, K. J. (2018). Should multiple imputation be the method of choice for handling missing data in randomized trials?. Statistical methods in medical research, 27(9), 2610-2626.
[2] Mixed model repeated measures (MMRM) in Stata, SAS and R – The Stats Geek

*1:添字は個人を示す記号です。よって、サンプルサイズがNの場合からまでの独立なN個のデータがあると考えてください。その他の変数も同様です。

*2:例えば年齢やBMIといった背景因子や、アウトカム変数そのものの介入前値などが考えられます。

*3:発生させたデータに「を掛けて」「を足す」という操作をすれば、平均、分散の正規分布からのサンプリングと同等になります。

*4:以下の平均の定義で、がアウトカムの平均に与える影響をそれぞれ0.3と設定しています。

*5:理論的にはどういう意味で0.3に近いのか（例えば、無限に同じ試験を繰り返した時の平均が0.3に近いのか、サンプルサイズを無限に増やした時に0.3に近くなるのか）を考える必要がありますが、筆者の手に余る話なのでここでは深く考えないことにします。

*6:交互作用を含めることで、時点1ではグループ間に差はないけれど時点2では差が生じている、という状況を表現することができます。

*7:長くなるので、詳細は参考文献[2]をご参照ください。

*8:題材の論文とは横軸の順番と色付けが異なります。うまく調整する方法は調べればあると思うのですが、本題と外れるので今回はそこまで踏み込んでいません。